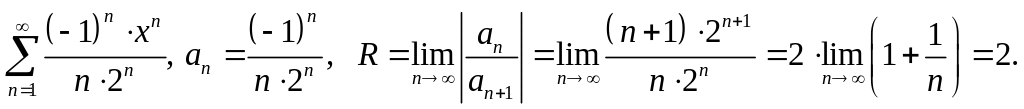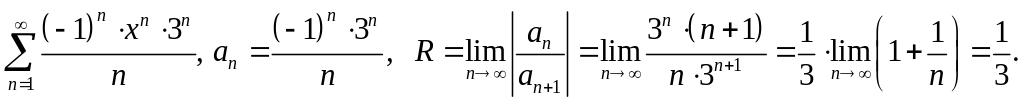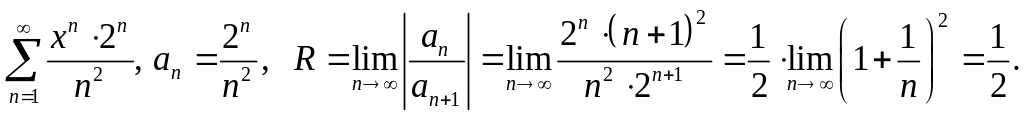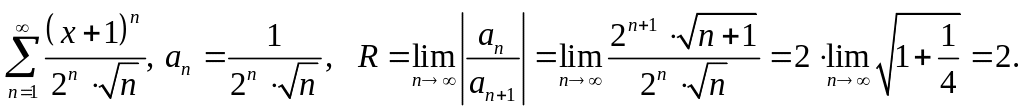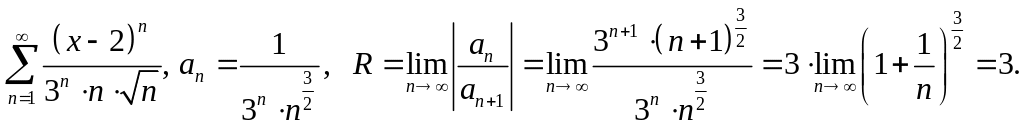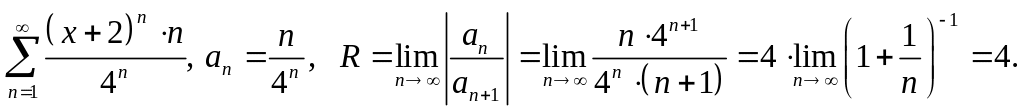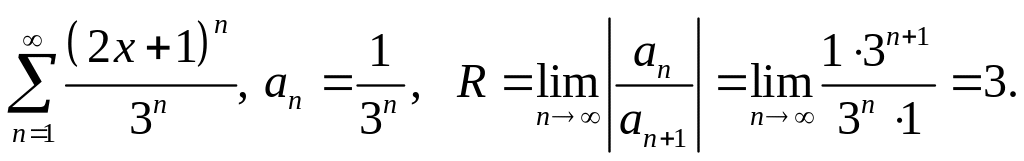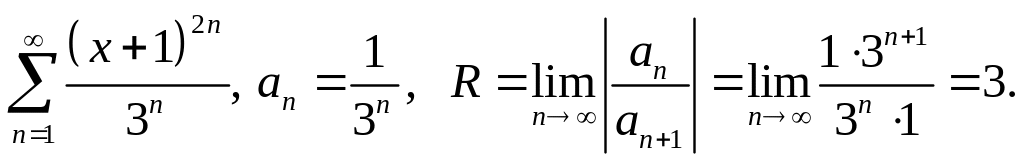Ряды найти интервал сходимости математический анализ амгу
.docВыполнить задание:
Найти интервал сходимости данных рядов

Прислать решенные задания в качестве ответа преподавателю.
Решение:
Интервал сходимости
![]() .
Проверим на сходимость концы интервала.
.
Проверим на сходимость концы интервала.
При
![]() получаем расходящийся гармонический
ряд
получаем расходящийся гармонический
ряд
![]() с показателем
с показателем
![]() .
.
При
![]() получаем сходящийся ряд Лейбница
получаем сходящийся ряд Лейбница
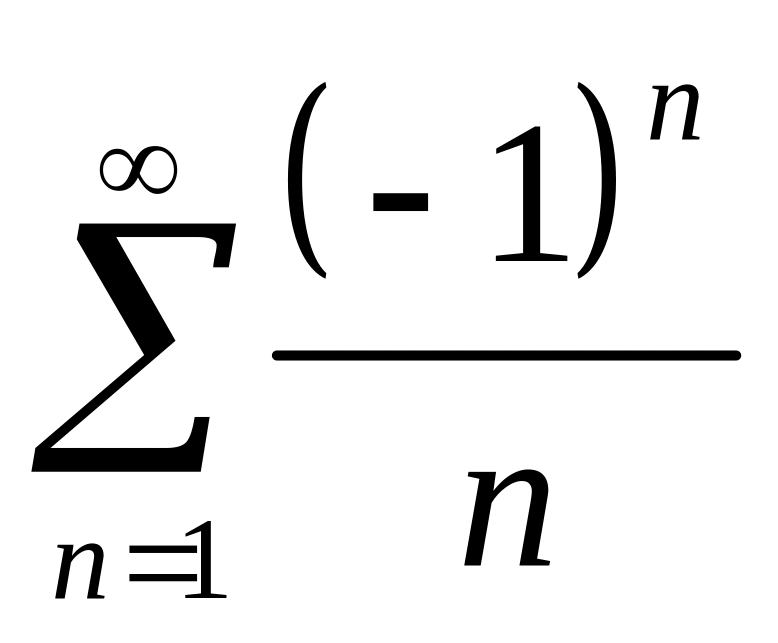 .
.
При этом сходимость – условная.
Ответ:
![]() .
.
Интервал сходимости
![]() .
Проверим на сходимость концы интервала.
.
Проверим на сходимость концы интервала.
При
![]() получаем расходящийся гармонический
ряд
с показателем
.
получаем расходящийся гармонический
ряд
с показателем
.
При
![]() получаем сходящийся ряд Лейбница
.
получаем сходящийся ряд Лейбница
.
При этом сходимость – условная.
Ответ:
![]() .
.
Интервал сходимости
![]() Проверим на сходимость концы интервала.
Проверим на сходимость концы интервала.
При
![]() получаем сходящийся ряд Лейбница
получаем сходящийся ряд Лейбница
 .
.
При этом сходимость – абсолютная.
При
![]() сходящийся гармонический ряд
с показателем
сходящийся гармонический ряд
с показателем
![]() .
.
Ответ:
![]()
Интервал сходимости
![]() .
Проверим на сходимость концы интервала.
.
Проверим на сходимость концы интервала.
При
![]() получаются ряды для которых не выполняется
необходимое условие сходимости
получаются ряды для которых не выполняется
необходимое условие сходимости
![]() т.е.
получаются расходящиеся ряды.
т.е.
получаются расходящиеся ряды.
Ответ: .
Интервал сходимости![]() .
Проверим на сходимость концы интервала.
.
Проверим на сходимость концы интервала.
При
![]() получаем сходящийся ряд Лейбница
получаем сходящийся ряд Лейбница
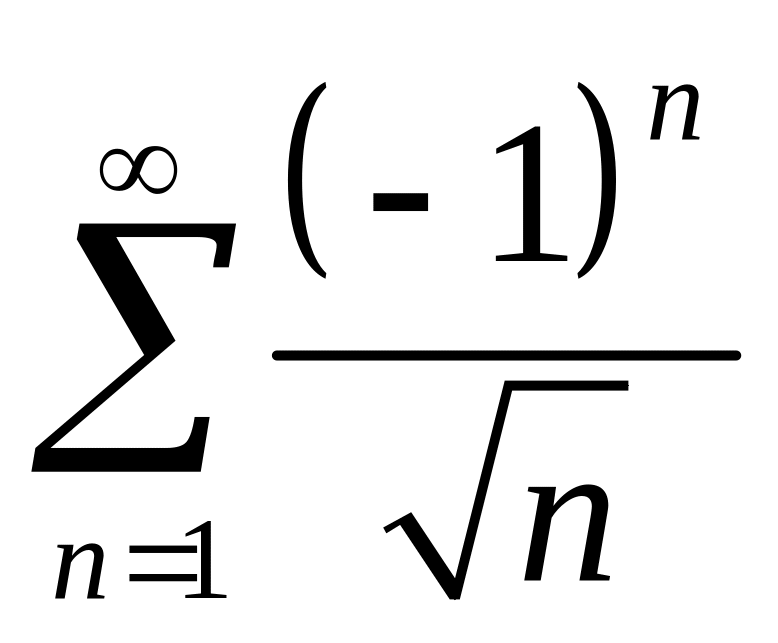 .
.
При этом сходимость – условная.
При
![]() получаем расходящийся гармонический
ряд
с показателем
получаем расходящийся гармонический
ряд
с показателем
![]() .
.
Ответ:
![]() .
.
Интервал сходимости
![]() Проверим на сходимость концы интервала.
Проверим на сходимость концы интервала.
При
![]() получаем сходящийся ряд Лейбница
получаем сходящийся ряд Лейбница
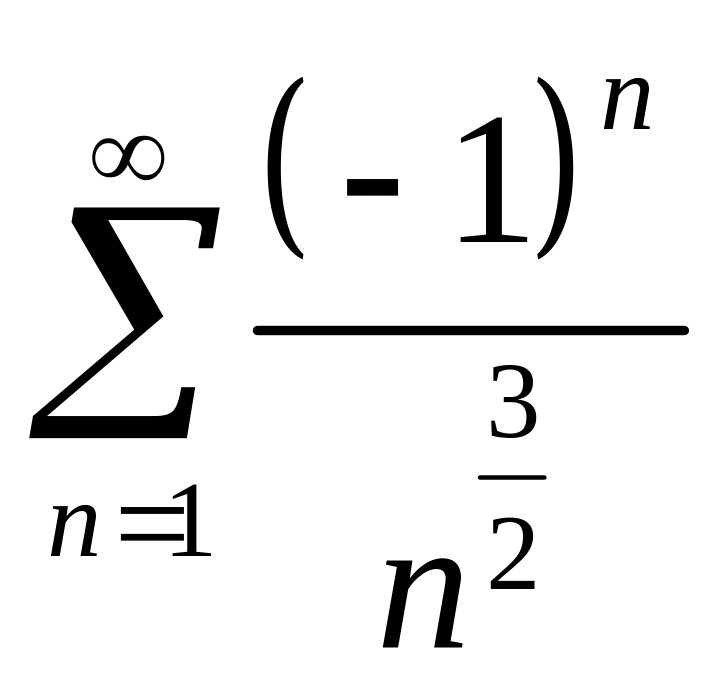 .
.
При этом сходимость – абсолютная.
При
![]() сходящийся гармонический ряд
с показателем
сходящийся гармонический ряд
с показателем
![]() .
.
Ответ:
![]()
Интервал сходимости
![]() Проверим на сходимость концы интервала.
Проверим на сходимость концы интервала.
При
![]() получаются ряды для которых не выполняется
необходимое условие сходимости
получаются ряды для которых не выполняется
необходимое условие сходимости
![]() т.е.
получаются расходящиеся ряды.
т.е.
получаются расходящиеся ряды.
Ответ:
![]() .
.
Интервал сходимости![]()
Проверим на сходимость концы интервала.
При
![]() получаются ряды для которых не выполняется
необходимое условие сходимости
получаются ряды для которых не выполняется
необходимое условие сходимости
![]() т.е.
получаются расходящиеся ряды.
т.е.
получаются расходящиеся ряды.
Ответ:
![]() .
.
Интервал сходимости
![]()
Проверим на сходимость концы интервала.
При
![]() получаются ряды для которых не выполняется
необходимое условие сходимости
т.е.
получаются расходящиеся ряды.
получаются ряды для которых не выполняется
необходимое условие сходимости
т.е.
получаются расходящиеся ряды.
Ответ:
![]() .
.
 Т.е. рассматриваем поведение степенного
ряда
Т.е. рассматриваем поведение степенного
ряда
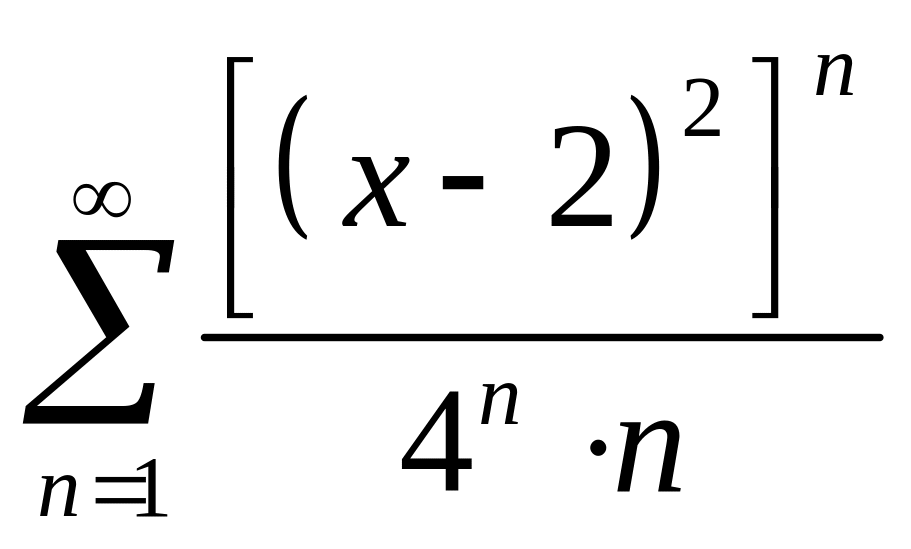 .
.
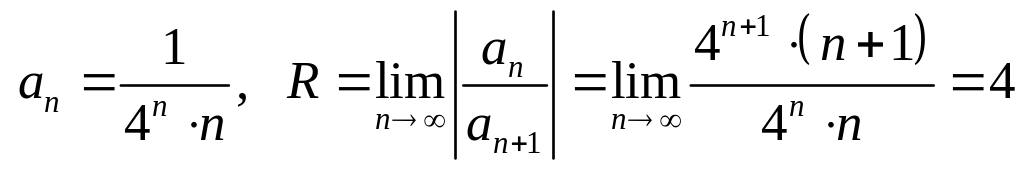
Интервал сходимости
![]()
Проверим на сходимость концы интервала.
При
![]() получаем расходящийся гармонический
ряд
с показателем
.
получаем расходящийся гармонический
ряд
с показателем
.
Ответ:
![]() .
.