№9 лабораторная МП

Федеральное агентство связи Ордена

Трудового Красного Знамени

федеральное бюджетное образовательное учреждение высшего образования

«Московский Технический Университет Связи и Информатики»

(МТУСИ)

Кафедра Информатики

Предмет: Введение в математические пакеты прикладных программ

Лабораторная работа по ВвМППП № 9

Тема:

«Технология решения задач многомерной оптимизации средствами Scilab»

Вариант 00

Выполнил:

Великий преподаватель

__________________________

Москва 0000

Общее задание

1. Изучите материал Темы 2.6 (п. 2.6.1).

2. Выберите индивидуальное задание из табл. 2.6.2-1.

3. Постройте график функции F(x₁,х₂);

4. Создайте для использования функции optim() вспомогательную функцию costf(), необходимую для вычисления значений целевой функции и её частных производных.

5. Найдите координаты точки минимум функции F(x₁,х₂) с использованием встроенной функций optim();

6. Получите значение функции, значений ее параметров, обеспечивающих оптимальное значение и частных производных в точке минимума.

7. Сохраните текст рабочего окна на внешнем носителе.

8. Предоставьте результаты работы преподавателю, ответить на поставленные вопросы.

9. Оформить отчет по выполненной работе.

//Лабораторная работа по теме:"Технология решения задач многомерной оптимизации средствами Scilab"

// Выполнил:

//Вариант --

//Создание матрицы значений аргументов функции z(x1;x2)

[x1 x2]=meshgrid(-1:0.1:1,-1:0.1:1);

//Описание функции z(x1,x2)

deff('y=z(x1,x2)','y=2.*x1.^2+x2.^2+2*x1.*x2+x1-12')

//Построение графика функции z(x1,x2)

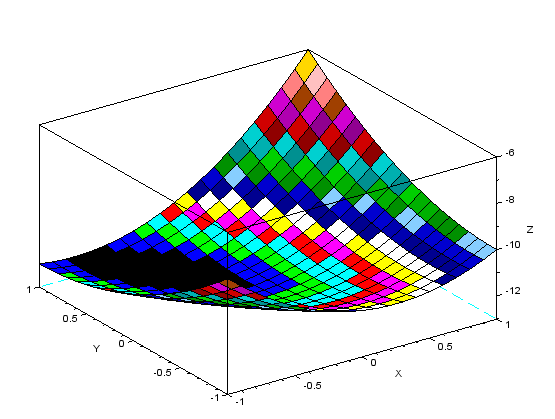
surf(x1,x2,z(x1,x2))

//Создание вспомогательной функции costf() для использование функции optim()

function [y]=gg(x)

> y=2.*x(1).^2+x(2).^2+2*x(1).*x(2)+x(1)-12

> endfunction

function [f,g,ind]=cst(x,ind)

> f=gg(x)

> g=numderivative(gg,x);

> endfunction

//Задание вектора начальных приближений

x0=[-1;1];

//Поиск координат минимума многомерной функции

f,xopt]=optim(cst,x0)

xopt =

-0.5

0.5

f =

-12.25

//Получение значений частных производных в точке минимума

numderivative(gg,xopt)

ans =

0. 0.