
- •Высшая математика
- •1. Функции, область определения и изменения функций. Обратные функции. Пределы функций, односторонние пределы.
- •2. Свойства пределов, виды неопределённостей, способы их раскрытия.
- •3. Первый и второй замечательные пределы. Основание натуральных логарифмов.
- •4. Производные функций. Свойства производных, их смысл.
- •5. Производные произведения и отношения двух функций.
- •6. Производные сложной и обратной функции.
- •7. Производные основных элементарных функций.
- •8. Производные высших порядков.
- •Решение.
- •9. Неопределённые интегралы, их смысл и свойства.
- •10. Замена переменных в неопределённых интегралах, интегрирование по частям.
- •11. Внесение части подынтегрального выражения под знак дифференциала.
- •12. Универсальная тригонометрическая подстановка.
- •13. Интегрирование дробно-рациональных выражений. Интегрирование выражений, содержащих квадратные трехчлены и корни квадратные из них.
- •14. Функция 2-х переменных, способы их представления, частные производные. Дифференциал функций 2-х переменных, градиент.
- •15. Приближенные вычисления значений функций с помощью дифференциалов.
5. Производные произведения и отношения двух функций.
Ответ.
(u(x)⋅v(x))′=u′(x)v(x)+u(x)v′(x).
Производная
произведения
равна производная первой функции на
вторую плюс первая функция, умноженная
на производную второй. Пример.
Найти производную функции y(x)=xsinx. Так
как заданная функция есть произведением
двух функций u(x)=x и v(x)=sinx, то производную
y′(x) находим как от произведения. Согласно
формуле имеем:
y′(x)=(xsinx)′=(x)′⋅sinx+x⋅(sinx)′=$$=1⋅sinx+x⋅cosx=sinx+xcosx.
Ответ. y′(x)=sinx+xcosx. Если функции
![]() и
и
![]() дифференцируемы в некоторой точке
дифференцируемы в некоторой точке
![]() и
и
![]() ,
то в этой точке дифференцируемо и их
частное u/v, причём
,
то в этой точке дифференцируемо и их
частное u/v, причём
![]() .
т.е. производная частного
двух
функций равна дроби, числитель которой
есть разность произведений знаменателя
на производную числителя и числителя
на производную знаменателя, а знаменатель
есть квадрат прежнего числителя.
.
т.е. производная частного
двух
функций равна дроби, числитель которой
есть разность произведений знаменателя
на производную числителя и числителя
на производную знаменателя, а знаменатель
есть квадрат прежнего числителя.
6. Производные сложной и обратной функции.
Ответ.
Дифференцирование сложной функции:
![]() .
Прежде всего, обратим внимание на запись
.
Прежде всего, обратим внимание на запись
![]() .
Здесь у нас две функции –
.
Здесь у нас две функции –
![]() и
и
![]() ,
причем функция
,
образно говоря, вложена в функцию
.
Функция такого вида (когда одна функция
вложена в другую) и называется сложной
функцией.
Пример.
Найти производную функции
,
причем функция
,
образно говоря, вложена в функцию
.
Функция такого вида (когда одна функция
вложена в другую) и называется сложной
функцией.
Пример.
Найти производную функции
![]() .
Представим, что нам нужно вычислить
значение выражения
.
Представим, что нам нужно вычислить
значение выражения
![]() при
при
![]() (вместо
единицы может быть любое число). В первую
очередь нужно будет выполнить следующее
действие:
(вместо
единицы может быть любое число). В первую
очередь нужно будет выполнить следующее
действие:
![]() ,
поэтому многочлен
,
поэтому многочлен
![]() и
будет функцией:
.
и
будет функцией:
.

Во
вторую очередь нужно будет найти
![]() ,
поэтому синус – будет функцией:
,
поэтому синус – будет функцией:
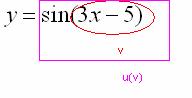
После
этого нужно применить правило
дифференцирования сложной функции
.
Начинаем решать – заключаем всю функцию
в скобки и ставим справа вверху штрих:
![]() Сначала
находим производную функции
Сначала
находим производную функции
![]() (синуса),
смотрим на таблицу производных
элементарных функций и замечаем, что
(синуса),
смотрим на таблицу производных
элементарных функций и замечаем, что
![]() .
Все табличные шаблоны применимы и в том
случае, если «икс» заменить любой
дифференцируемой функцией
.
В данном примере вместо «икс»:
.
.
Все табличные шаблоны применимы и в том
случае, если «икс» заменить любой
дифференцируемой функцией
.
В данном примере вместо «икс»:
.
![]() .
Функция
.
Функция
![]() не
изменилась. Очевидно, что
не
изменилась. Очевидно, что
![]() .
Результат применения формулы
в
чистовом оформлении выглядит так:
.
Результат применения формулы
в
чистовом оформлении выглядит так:
![]() .
Далее производная второй функции:
.
Далее производная второй функции:
![]() .
Постоянный множитель обычно выносят в
начало выражения:
.
Постоянный множитель обычно выносят в
начало выражения:
![]() .
Готово. Производная
обратной
функции.
.
Готово. Производная
обратной
функции.
![]()

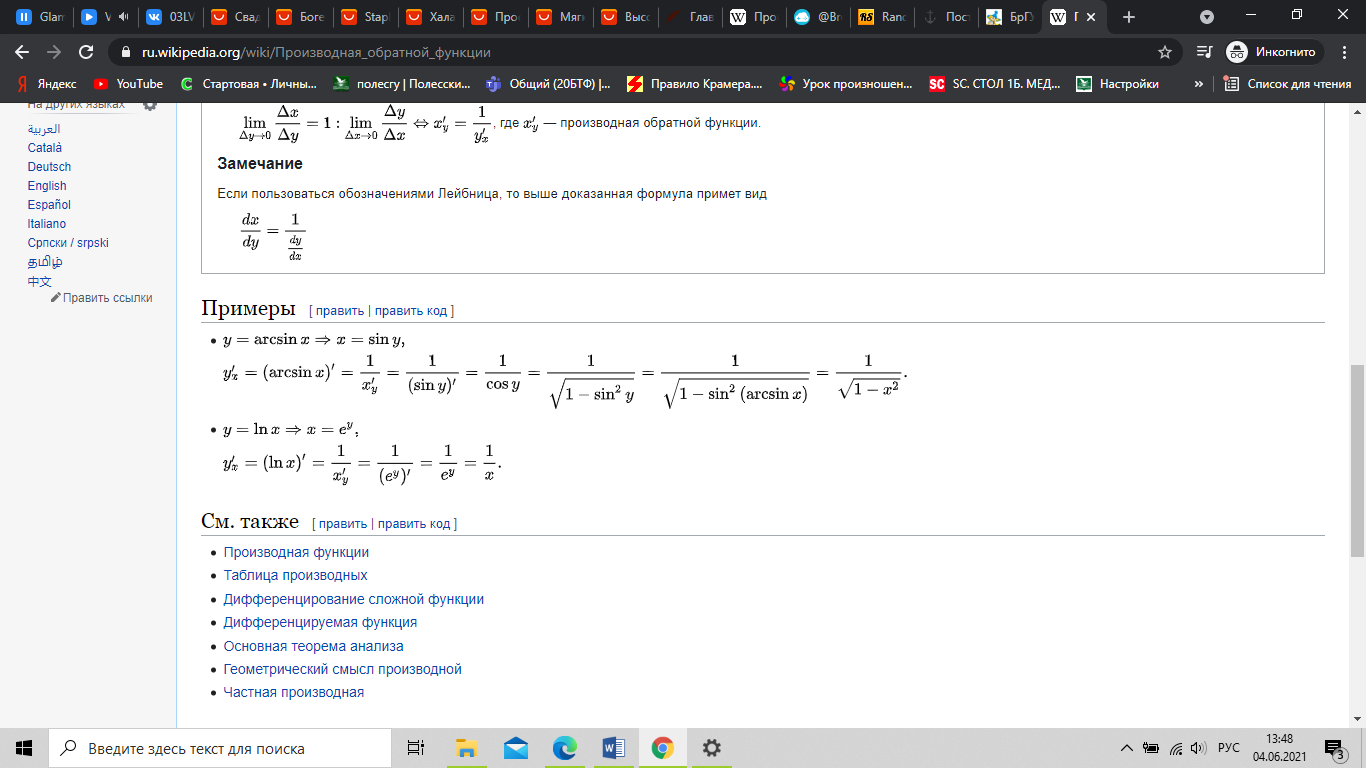
Примеры.
7. Производные основных элементарных функций.
Ответ. Элементарные функции — функции, которые можно получить с помощью конечного числа арифметических действий и композиций из следующих основных элементарных функций: степенная функция с любым действительным показателем; показательная и логарифмическая функции; тригонометрические и обратные тригонометрические функции. Каждую элементарную функцию можно задать формулой, то есть набором конечного числа символов, соответствующих используемым операциям. Все элементарные функции непрерывны на своей области определения. Иногда к основным элементарным функциям относят также гиперболические и обратные гиперболические функции, хотя они могут быть выражены через перечисленные выше основные элементарные функции.
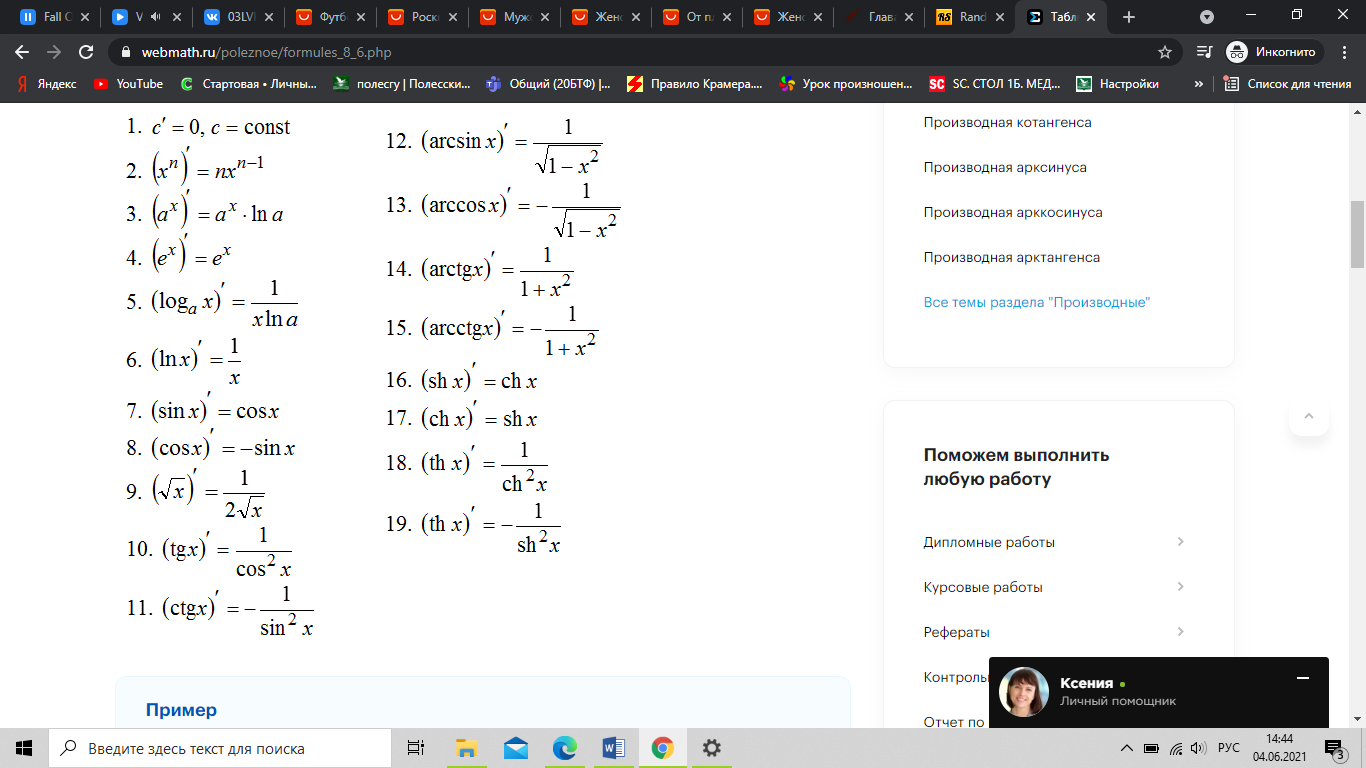
Формулы:
8. Производные высших порядков.
Ответ.
Вот функция:
![]() и
вот её первая производная:
и
вот её первая производная:
![]() .
Вторая производная – это производная
от 1-й производной:
.
Вторая производная – это производная
от 1-й производной:
![]() .
Вторую
производную уже считают производной
высшего
порядка.
Аналогично: третья производная – это
производная от 2-й производной:
.
Вторую
производную уже считают производной
высшего
порядка.
Аналогично: третья производная – это
производная от 2-й производной:
![]() .
Четвёртая производная – есть производная
от 3-й производной:
.
Четвёртая производная – есть производная
от 3-й производной:
![]() .
Пятая производная:
.
Пятая производная:
![]() ,
и очевидно, что все производные более
высоких порядков тоже будут равны нулю:
,
и очевидно, что все производные более
высоких порядков тоже будут равны нулю:
![]() .
Помимо римской нумерации на практике
часто используют следующие обозначения:
.
Помимо римской нумерации на практике
часто используют следующие обозначения:
![]() ,
производную же «энного» порядка
обозначают через
,
производную же «энного» порядка
обозначают через
![]() .
При этом надстрочный индекс нужно
обязательно заключать в скобки – чтобы
отличать производную от «игрека» в
степени. Иногда встречается такая
запись:
.
При этом надстрочный индекс нужно
обязательно заключать в скобки – чтобы
отличать производную от «игрека» в
степени. Иногда встречается такая
запись:
![]() – третья, четвёртая, пятая, …, «энная»
производные соответственно. Пример.
Дана функция
– третья, четвёртая, пятая, …, «энная»
производные соответственно. Пример.
Дана функция
![]() .
Найти
.
Найти
![]() .
.
