
- •Высшая математика
- •1. Функции, область определения и изменения функций. Обратные функции. Пределы функций, односторонние пределы.
- •2. Свойства пределов, виды неопределённостей, способы их раскрытия.
- •3. Первый и второй замечательные пределы. Основание натуральных логарифмов.
- •4. Производные функций. Свойства производных, их смысл.
- •5. Производные произведения и отношения двух функций.
- •6. Производные сложной и обратной функции.
- •7. Производные основных элементарных функций.
- •8. Производные высших порядков.
- •Решение.
- •9. Неопределённые интегралы, их смысл и свойства.
- •10. Замена переменных в неопределённых интегралах, интегрирование по частям.
- •11. Внесение части подынтегрального выражения под знак дифференциала.
- •12. Универсальная тригонометрическая подстановка.
- •13. Интегрирование дробно-рациональных выражений. Интегрирование выражений, содержащих квадратные трехчлены и корни квадратные из них.
- •14. Функция 2-х переменных, способы их представления, частные производные. Дифференциал функций 2-х переменных, градиент.
- •15. Приближенные вычисления значений функций с помощью дифференциалов.
2. Свойства пределов, виды неопределённостей, способы их раскрытия.
Ответ.
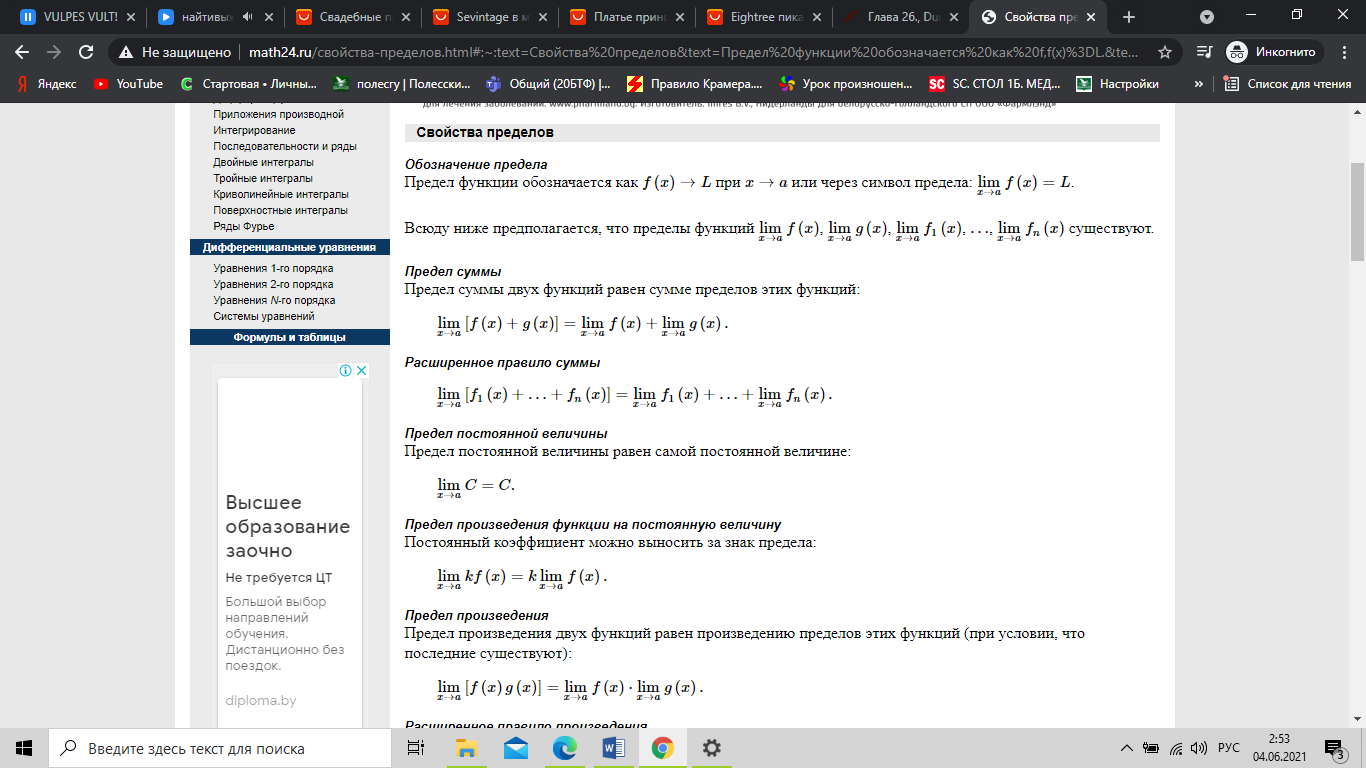
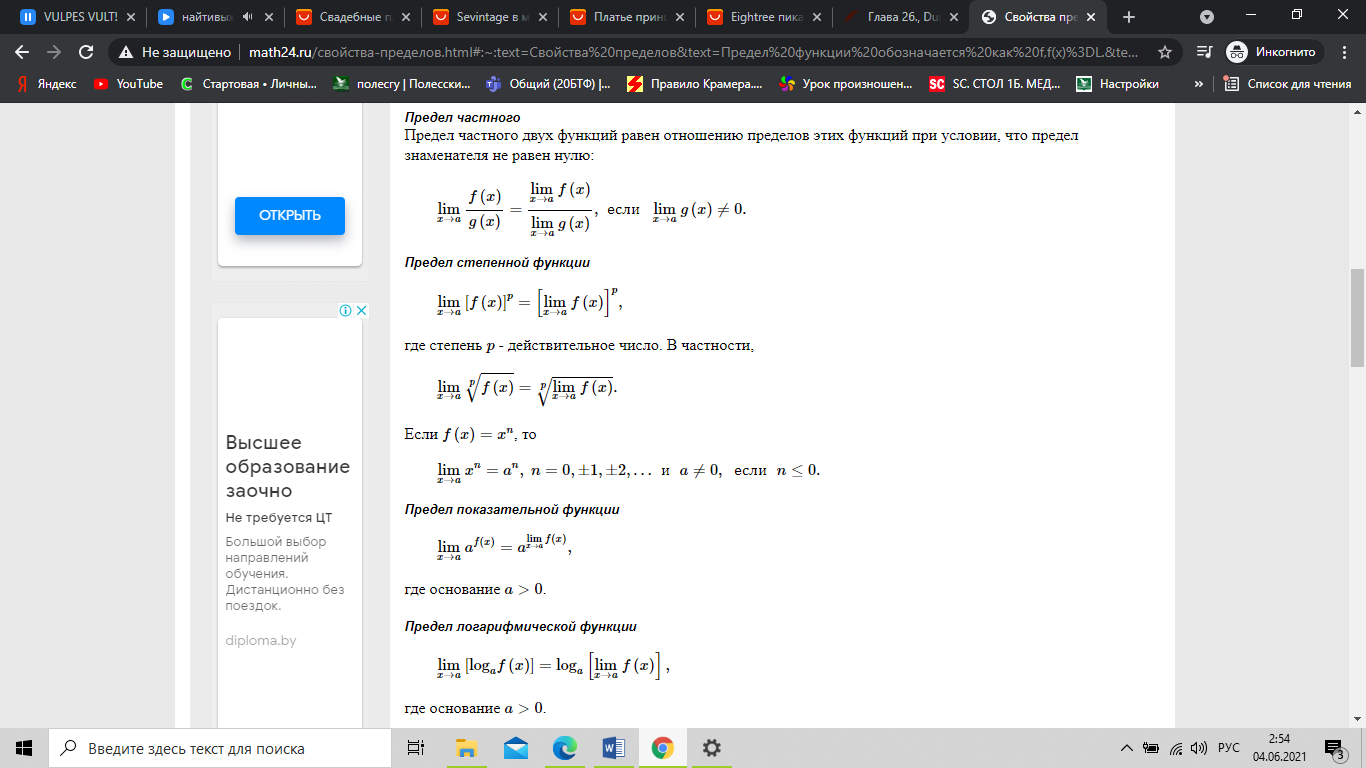
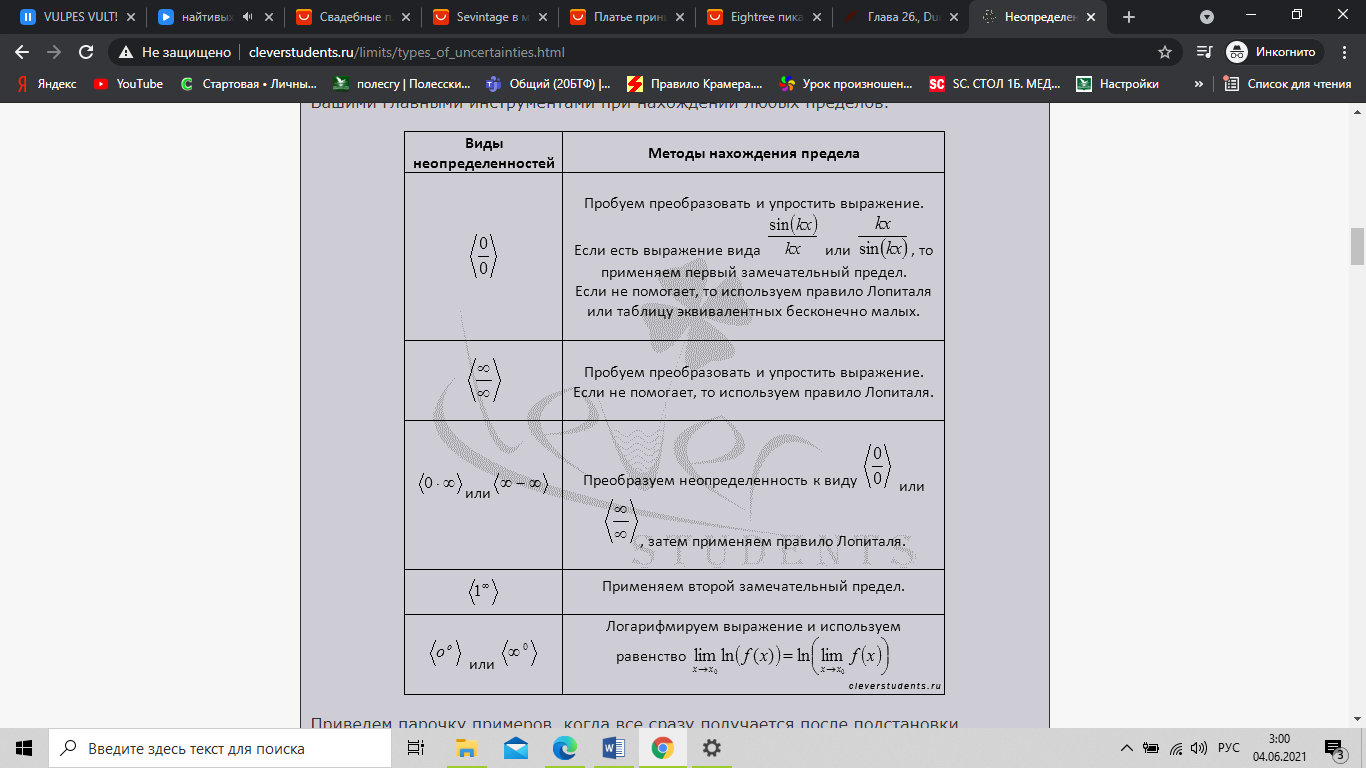
Основные виды неопределенностей: ноль делить на ноль, бесконечность делить на бесконечность, ноль умножить на бесконечность, бесконечность минус бесконечность, единица в степени бесконечность, ноль в степени ноль, бесконечность в степени ноль. Все другие выражения неопределённостями не являются и принимают вполне конкретное конечное или бесконечное значение. Раскрывать неопределенности позволяет: упрощение вида функции (преобразование выражения с использованием формул сокращенного умножения, тригонометрических формул, домножением на сопряженные выражения с последующим сокращением и т.п.); использование замечательных пределов; применение правила Лопиталя; использование замены бесконечно малого выражения ему эквивалентным. Каждому виду неопределенности поставим в соответствие метод ее раскрытия (метод нахождения предела).
3. Первый и второй замечательные пределы. Основание натуральных логарифмов.
Ответ.
Рассмотрим следующий предел:
![]() .
Согласно правилу нахождения пределов
пробуем подставить ноль в функцию: в
числителе у нас получается ноль (синус
нуля равен нулю), в знаменателе, очевидно,
тоже ноль. Таким образом, мы сталкиваемся
с неопределенностью вида
.
Согласно правилу нахождения пределов
пробуем подставить ноль в функцию: в
числителе у нас получается ноль (синус
нуля равен нулю), в знаменателе, очевидно,
тоже ноль. Таким образом, мы сталкиваемся
с неопределенностью вида
![]() ,
которую раскрывать не нужно. В курсе
математического анализа, доказывается,
что:
,
которую раскрывать не нужно. В курсе
математического анализа, доказывается,
что:
![]() Данный
математический факт носит название
Первого
замечательного
предела.
Функции могут быть расположены по-другому,
это ничего не меняет:
Данный
математический факт носит название
Первого
замечательного
предела.
Функции могут быть расположены по-другому,
это ничего не меняет:
![]() – тот же самый первый замечательный
предел. На практике в качестве параметра
может выступать не только переменная,
но и элементарная функция, сложная
функция. Важно лишь, чтобы она стремилась
к нулю. В теории математического анализа
доказано, что:
– тот же самый первый замечательный
предел. На практике в качестве параметра
может выступать не только переменная,
но и элементарная функция, сложная
функция. Важно лишь, чтобы она стремилась
к нулю. В теории математического анализа
доказано, что:
![]() .
Данный факт носит название второго
замечательного
предела.
Справка:
.
Данный факт носит название второго
замечательного
предела.
Справка:
![]() – это иррациональное число. В качестве
параметра может выступать не только
переменная , но и сложная функция. Важно
лишь, чтобы она стремилась к бесконечности.
Натуральным
логарифмом
называется логарифм по основанию e.
Такие логарифмы обозначаются символом
ln. Запись lnx означает тоже самое, что и
logex. Основание натурального логарифма
- число е. Свойства
и основные
формулы
натурального логарифма. 1) ln1=0. Натуральный
логарифм единицы равен нулю (Заметим,
что логарифм по любому основанию от 1
равен 0). 2) lne=1. 3) ln(xy)=lnx+lny. 4) lnxy=lnx−lny. 5)
lnxn=n⋅lnx.
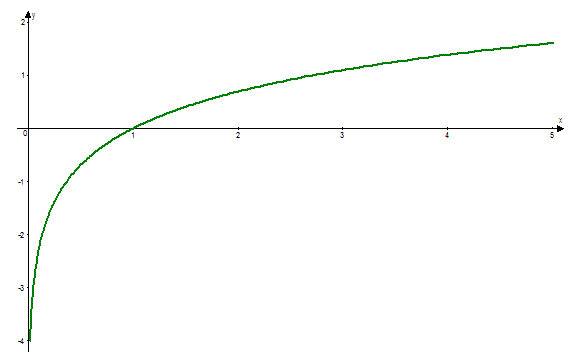
6) График функции y=lnx:
– это иррациональное число. В качестве
параметра может выступать не только
переменная , но и сложная функция. Важно
лишь, чтобы она стремилась к бесконечности.
Натуральным
логарифмом
называется логарифм по основанию e.
Такие логарифмы обозначаются символом
ln. Запись lnx означает тоже самое, что и
logex. Основание натурального логарифма
- число е. Свойства
и основные
формулы
натурального логарифма. 1) ln1=0. Натуральный
логарифм единицы равен нулю (Заметим,
что логарифм по любому основанию от 1
равен 0). 2) lne=1. 3) ln(xy)=lnx+lny. 4) lnxy=lnx−lny. 5)
lnxn=n⋅lnx.
6) График функции y=lnx:
4. Производные функций. Свойства производных, их смысл.
Ответ. Производная функции — понятие дифференциального исчисления, характеризующее скорость изменения функции в данной точке. Определяется как предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке). Процесс вычисления производной называется дифференцированием. Обратный процесс — нахождение первообразной — интегрирование.
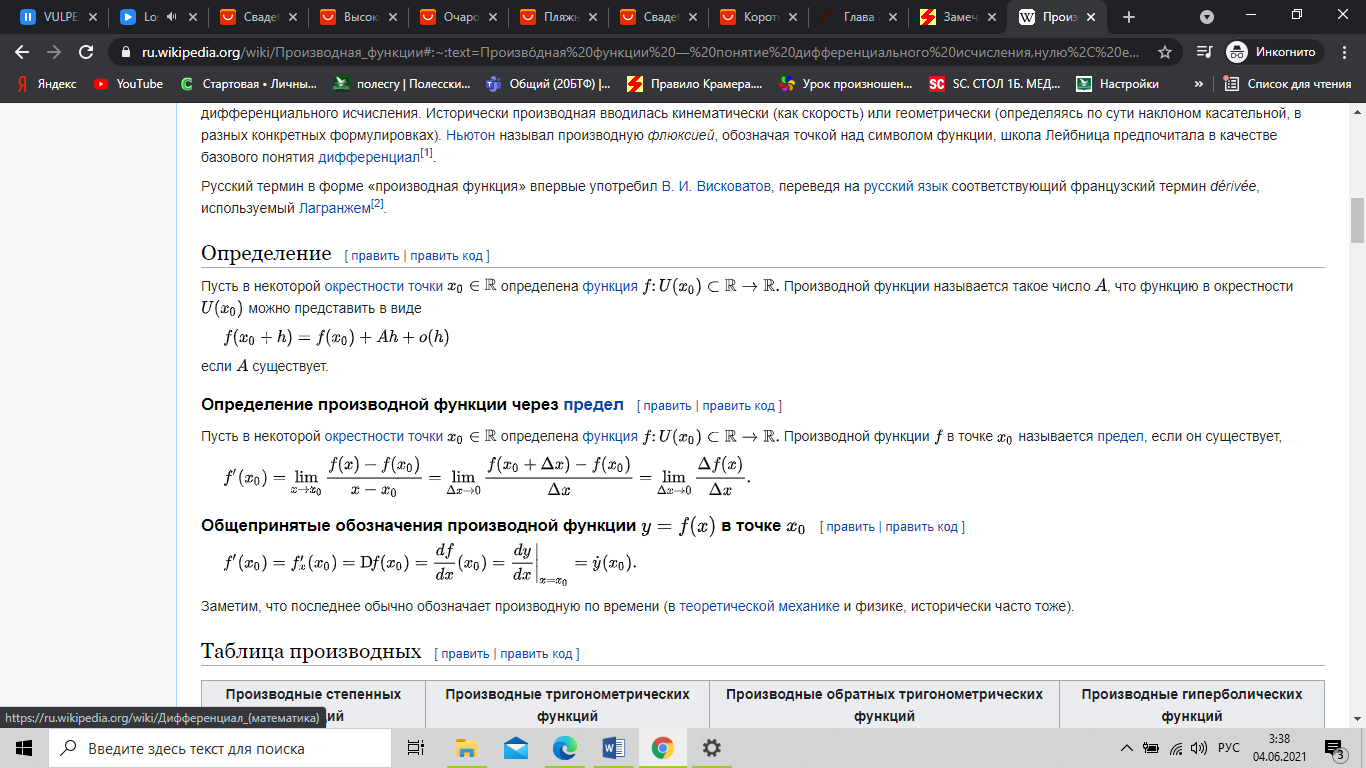
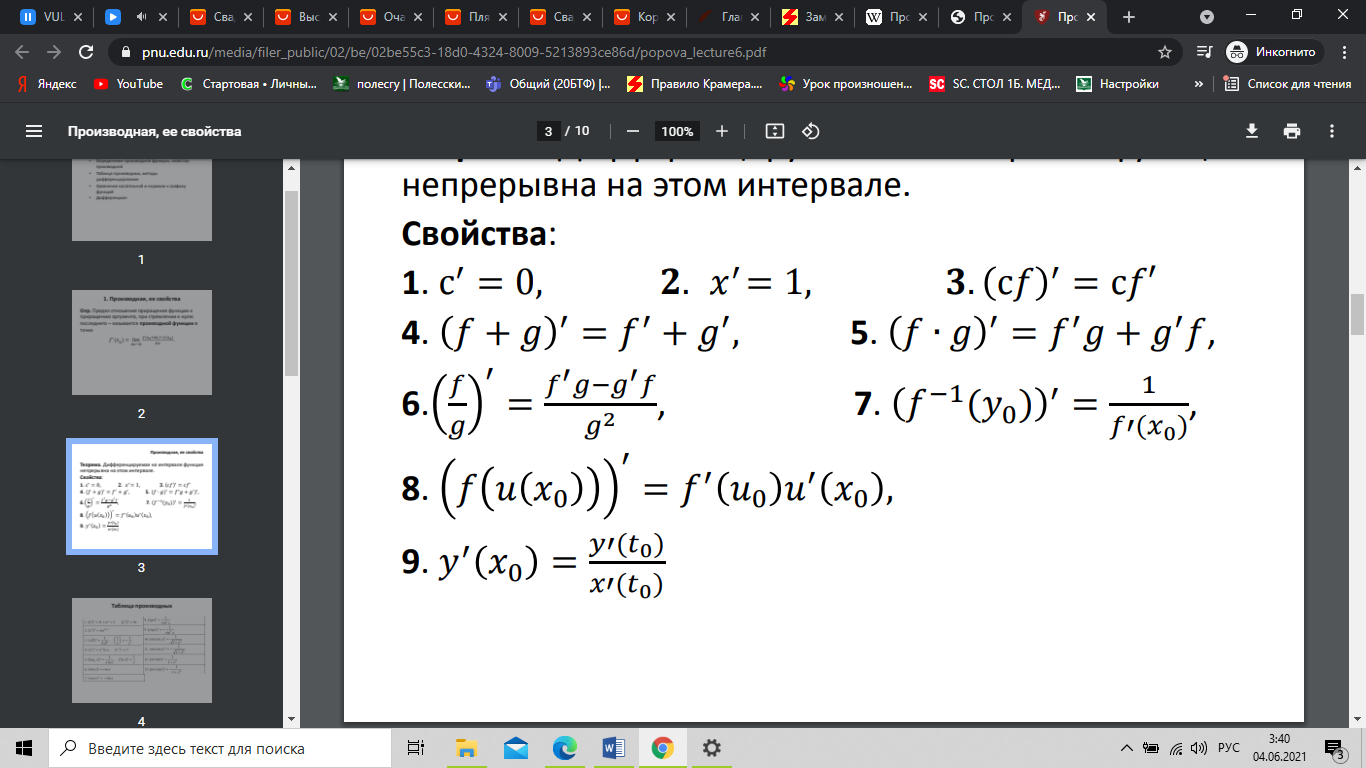
Геометрический смысл производной. Производная в точке x0 равна угловому коэффициенту касательной к графику функции y=f(x) в этой точке.
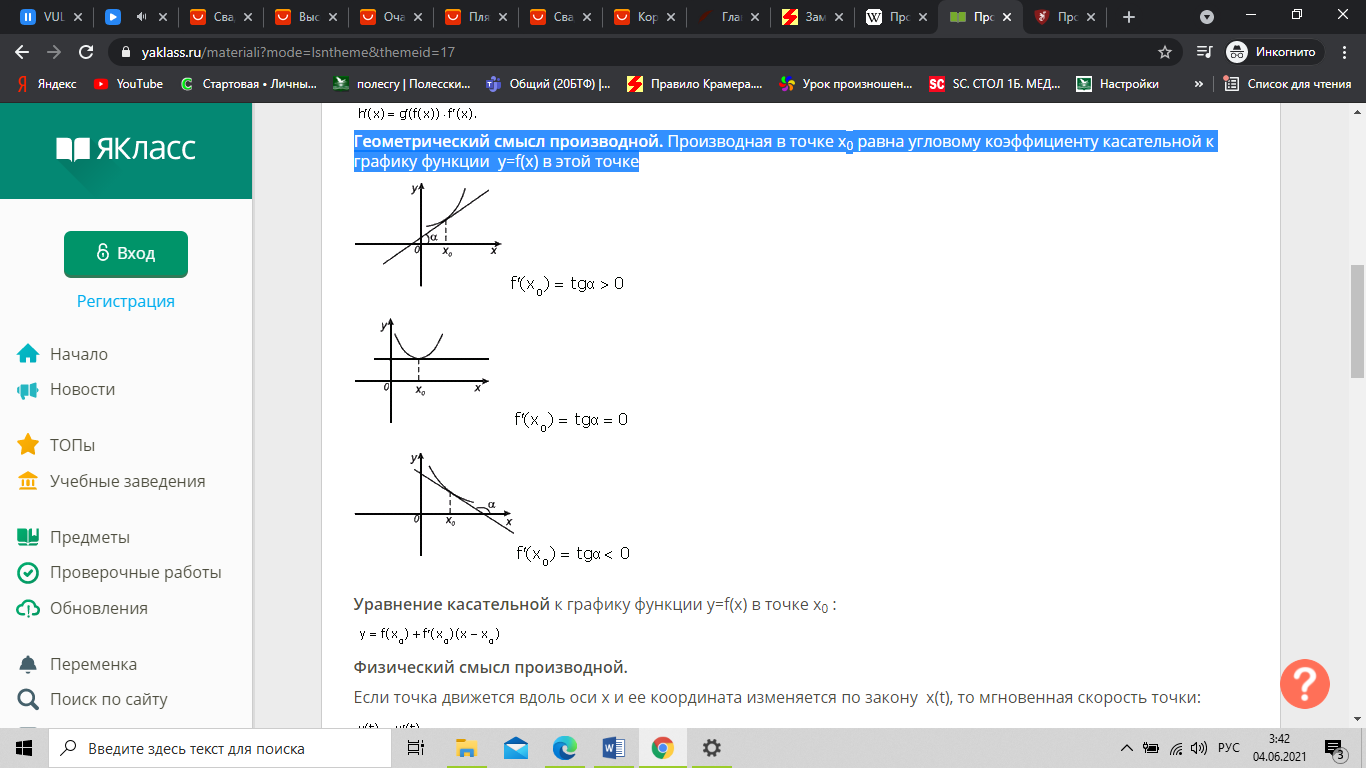
Физический
смысл
производной. Если точка движется вдоль
оси х и ее координата изменяется по
закону x(t), то мгновенная скорость точки:
![]() .
.
