Высшая математика

1. Функции, область определения и изменения функций. Обратные функции. Пределы функций, односторонние пределы.

Ответ. Совокупность всех тех значений, которые принимает аргумент х функции y = f (x), называется областью определения этой функции. Совокупность всех тех значений, которые принимает сама функция у, называется областью изменения этой функции. Обратная функция — функция, обращающая зависимость, выражаемую данной функцией. Например, если функция от x даёт y, то обратная ей функция от y даёт x. Обратная функция функции f обычно обозначается f^-1, иногда также используется обозначение f ^inv. Функция, имеющая обратную, называется обратимой. Функция g:Y→ X называется обратной к функции f:X→Y, если выполнены следующие тождества:

Чтобы найти обратную функцию, нужно решить уравнение y=f(x) относительно x. Если оно имеет более чем один корень, то функции, обратной к f не существует. Таким образом, функция f(x) обратима на интервале (a;b) тогда и только тогда, когда на этом интервале она взаимно-однозначна. Для непрерывной функции F(y) выразить y из уравнения x-F(y)=0 возможно в том и только том случае, когда функция F(y) строго монотонна. Тем не менее, непрерывную функцию всегда можно обратить на промежутках её строгой монотонности. Например, 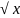является обратной функцией к х² на [0,+∞), хотя на промежутке (-∞,0] обратная функция другая: - x. Для существования обратной функции не являются необходимыми ни непрерывность, ни монотонность исходной функции. Непрерывная функция — функция, которая меняется без мгновенных «скачков» (называемых разрывами), то есть такая, малые изменения аргумента которой приводят к малым изменениям значения функции. График непрерывной функции является непрерывной линией. Монотонная функция — функция одной переменной, определённая на некотором подмножестве действительных чисел, которая либо везде (на области своего определения) не убывает, либо везде не возрастает. Предел функции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится значение рассматриваемой функции при стремлении её аргумента к данной точке. Предел функции является обобщением понятия предела последовательности: изначально под пределом функции в точке понимали предел последовательности элементов области значений функции, являющихся образами точек такой последовательности элементов области определения функции, которая сходится к точке, в которой рассматривается предел. Если такой предел существует, то говорят, что функция сходится к указанному значению, иначе говорят, что функция расходится. То, что предел функции рассматривается только в точках, предельных для области определения функции, означает, что в каждой окрестности данной точки есть точки области определения. Это позволяет говорить о стремлении аргумента функции к данной точке. Предельная точка области определения не обязана принадлежать самой области определения: например, можно рассматривать предел функции на концах открытого интервала, на котором определена функция (сами концы интервала в область определения не входят). В общем случае необходимо точно указывать способ сходимости функции. Отсутствие предела функции в данной точке означает, что для любого заранее заданного значения области значений существует окрестность этого значения такая, что в любой сколь угодно малой окрестности точки, в которой функция принимает заданное значение, существуют точки, значение функции в которых окажется за пределами указанной окрестности. Если в некоторой точке области определения функции существует предел и этот предел равен значению функции в данной точке, то функция называется непрерывной в данной точке. Односторонний предел — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторонним пределом (или пределом слева) и правосторонним пределом (пределом справа).