2021, 3-й курс / зачёт / зачёт практика
.pdf
Пункты допуска по рекурсивным фильтрам до АЧХ (включительно)
Уравнение рекурсивного ЦФ 1-го порядка выглядит следующим образом:
(1)
Системная функция записывается в виде:
(2)
Применив к обеим частям уравнение Z-преобразование и его свойства (линейности и смещения), получим:
Перенесем первую часть уравнения в левою сторону и получим:
Получаем:
(3)
где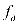 
– частота дискретизации, 
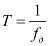– интервал дискретизации Найдем 
:
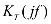(4)
Найдем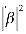 
:
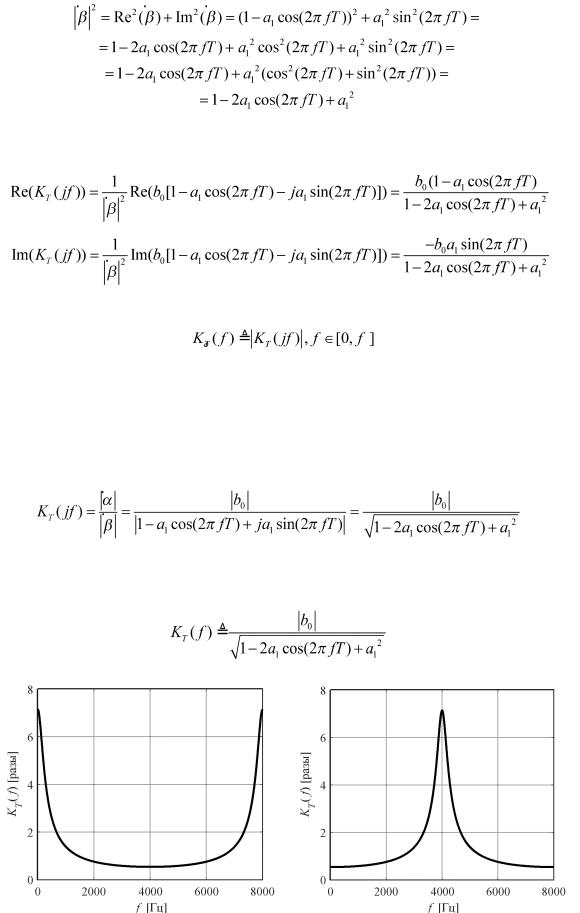
Далее найдем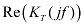 
и 
:
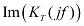АЧХ называется функция частоты:
(5)
где 
- оператор взятия модуля комплексного числа
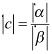получаем:
Преобразуем знаменатель с учетом полученного ранее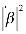 
и получим:
Рис.1 – для а1 > 0 |
Рис.2 – для a1 < 0 |
Неканоническая схема ЦФ
Каноническая схема ЦФ
Рекурсивный фильтр 2-го порядка.
Проверка на устойчивость:
1) |
– 1 < a1 < 1 |
; |
-1 < 0.4 < 1 |
2) |
a2+a1 < 1 |
; |
0.7 < 1 |
3) |
a2-a1 < 1 |
; |
0.1 < 1 |
Фильтр устойчив.
Преимуществом канонической схемы фильтра является минимальное число элементов задержки, равное порядку фильтра. Благодаря этому сокращается общий объем вычислений.
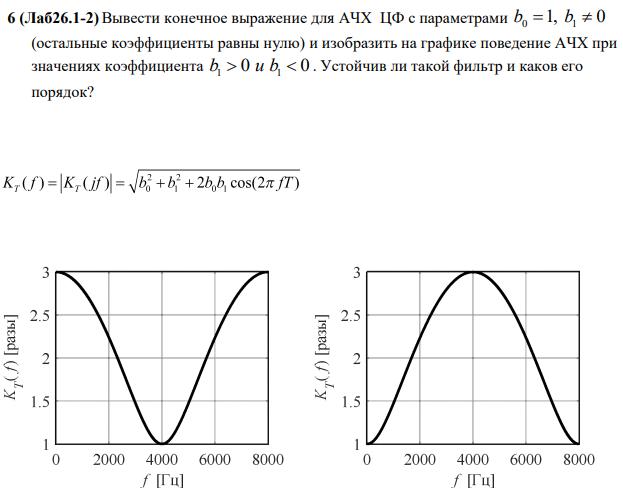
АЧХ
|
|
b1>0 |
b1<0 |
|
|
Устойчивый фильтр, т.к. нерекурсивный фильтр 1-го порядка (знаменатель системной функции = 0).
7 (Лаб26.1-2) Записать общее разностное уравнение ЦФ, его системную функцию. Как определяются порядок цифрового фильтра, нули и полюса передаточной функции, какой фильтр называется нерекурсивным и