25ргзтймс
.docxМІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
Одеський національний морський університет
Навчально-науковий інституту морського бізнесу
Факультет транспортних технологій і систем
Кафедра «Управління логістичними системами і проектами»
ТЕОРІЯ ЙМОВІРНОСТІ І
МАТЕМАТИЧНОЇ СТАТИСТИКИ
РОЗРАХУНКОВО-ГРАФІЧНА РОБОТА
Варіант 6
Виконала:
ст. 2 курсу, 5 групи Гаврилюк
О. Д. Перевірив:
Зміст:
-
1.
Вихідні данні…………………………………………………….
3
2.
Основна частина (З1)……………………………………………
3
а) висновок……………………………………………………….
6
3.
Основна частина (З2)……………………………………………
8
б) висновок………………………………………………………
9
Варіант 6
Задача 1: Оцінка нормальності розподілу
В ОНМУ у двох групах відбулося тестування з логістики, яке оцінювалося за шкалою з максимальною оцінкою 60 балів. Необхідно проаналізувати результати тестування, збудувати варіаційний ряд, гістограму. Висунути гіпотезу про вид закону розподілу. Підібрати параметри закону розподілу (рівні їх оцінкам з урахуванням досвідчених даних). За допомогою критерію згоди перевірити, чи узгоджується гіпотеза з досвідченими даними. Рівень значимості взяти, що дорівнює 0,05.
Група 1 |
Група 2 |
|||||||||
28 |
24 |
20 |
18 |
48 |
20 |
18 |
14 |
28 |
3 |
|
26 |
48 |
38 |
18 |
14 |
28 |
18 |
14 |
28 |
20 |
|
14 |
24 |
26 |
30 |
24 |
16 |
18 |
24 |
20 |
18 |
|
20 |
30 |
40 |
18 |
30 |
26 |
14 |
34 |
18 |
32 |
|
40 |
30 |
28 |
23 |
30 |
40 |
22 |
29 |
33 |
15 |
|
37 |
42 |
37 |
16 |
46 |
20 |
15 |
40 |
15 |
24 |
|
23 |
37 |
30 |
30 |
28 |
42 |
29 |
50 |
22 |
33 |
|
32 |
26 |
19 |
32 |
23 |
24 |
26 |
37 |
55 |
60 |
|
Рішення: Оцінки по 1-2 гр. зведемо в одну сукупність і про ранжуємо.
Р. ряд. |
|||||||||
14 |
16 |
18 |
20 |
24 |
26 |
29 |
30 |
37 |
42 |
14 |
16 |
18 |
22 |
24 |
26 |
29 |
32 |
37 |
42 |
14 |
18 |
19 |
22 |
24 |
28 |
30 |
32 |
37 |
46 |
14 |
18 |
20 |
22 |
24 |
28 |
30 |
32 |
38 |
48 |
14 |
18 |
20 |
23 |
24 |
28 |
30 |
33 |
40 |
48 |
15 |
18 |
20 |
23 |
26 |
28 |
30 |
33 |
40 |
50 |
15 |
18 |
20 |
23 |
26 |
28 |
30 |
34 |
40 |
55 |
15 |
18 |
20 |
24 |
26 |
28 |
30 |
37 |
40 |
60 |
Для подальшого аналізу необхідно розбити ряд на інтервали.
Число інтервалів визначимо, використовуючи формулу Стерджису:
m = 1 + 3, 322 logn;
m = 1+3,322 log80=7,312
Розрахуємо величину інтервалу:
k
=
=
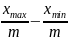= 6,291 = 6,3
Будуємо інтервали та записуємо частоту і час-ти вариант, потрапивших у інтервал: Т 1.1 – Визначення частот по интервалах:
№ інт. |
Інт. |
Частота |
Час-ти wi=ni/n |
|
Xi |
Xi+1 |
ni |
||
1 |
2 |
3 |
4 |
5 |
1 |
14 |
20,3 |
25 |
0,31 |
2 |
20,3 |
26,6 |
17 |
0,21 |
3 |
26,6 |
32,9 |
18 |
0,23 |
4 |
32,9 |
39,2 |
8 |
0,10 |
5 |
39,2 |
45,5 |
6 |
0,08 |
6 |
45,5 |
60 |
6 |
0,08 |
Сума |
80 |
1 |
||
Будуємо діограмму (гістограмму) вариаціоного ряду:
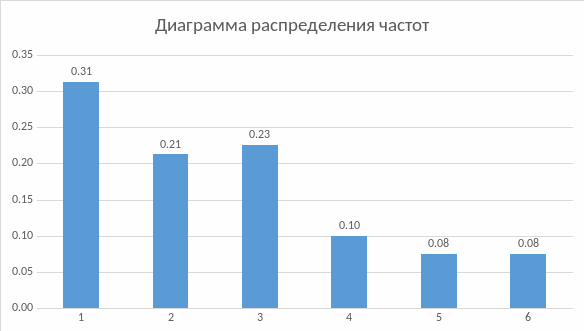
Рис. 1.1 Гістограма розподілу частот вибірки
По виду діаграми, висуваємо нульову гіпотезу H0 про нормальність розподілу за параметрами N (a, σ2):
Де а – середня ряду; σ2 – середньоквадратичне відхилення.
Знайдемо точкові оцінки параметрів розподілу. Для цього перейдемо до простого варіаційного ряду, вибираючи як варіиант середини інтервалів, складемо розрахункову таблицю, де:
6ст.: вибіркова середня
7ст.: інтервальні середні сума за стовпцем визначає середнє
варіаційного ряду;
8ст.: розрахунок інтервальної дисперсії (по рядках) та сума -
дисперсія варіаційного ряду.
Таким чином, припускаємо, що досліджувана величина має
нормальний закон розподілу з параметрами a = 3,98 та σ =0,89.
За допомогою критерію згоди Пірсона перевіримо, чи узгоджується
гіпотеза з досвідченими даними лише на рівні значимості α = 0,05 .
9-10ст.: розрахунок аргументу інтегральної функції Лапласа;
11-12ст.: значення функції Лапласа (за таблицями);
13ст.: розрахунок ймовірності попадання випадкової величини
відповідний інтервал. Сума по стовпцю має бути близькою до 1;
14ст.: розрахунок складової npi форули критерію. Де n = 80 - і кількість варіантів, а pi – інтервальна ймовірність.
15-16ст.: використовувати у разі потреби поєднання інтервалів
17ст.: інтервальний розрахунок x2 , сума по стовпцю визначає x2теорет.
=
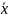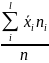= 2221,9/80 = 27,77 – середня
ряду;
S2
=
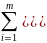= 634,44 – дисперсія
ряду;
S
=
=
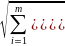= 25,19 –
середньоквадратичне
відхилення ряду;
X2
=
=
103,16 –
розрахунок теоретичного критерію, що
спостерігається.
За таблицею критичних значень xкр при рівні значущості α = 0,05 та числі ступенів свободи v = 5,3-3= 2,3 знайдемо xкр ≈ 7,8.
xкр = 7,8 xтеорет = 103,16, нульову гіпотезу про нормальний розподіл можна прийняти при цьому рівні значущості.
Т 1.2 – Точкови оцінки параметрів розподілу :
№ інт. |
Інт. |
Частота |
Час-ти wi=ni/n |
срдн X* |
a=X*wi |
S^2 = (X*-a)^2*wi |
(Xi-a)/S |
(Xi+1-a)/S |
Ф((Xi-a)/S) |
Ф((Xi+1-a)/S) |
Pi |
nPi |
ni |
nPi |
(ni-nPi)^2/nPi |
|
Xi |
Xi+1 |
ni |
||||||||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
1 |
14 |
20,3 |
25 |
0,31 |
17,15 |
5,36 |
43,44 |
0,20 |
0,34 |
0,08 |
0,13 |
0,05 |
4,30 |
25 |
4,30 |
99,49 |
2 |
20,3 |
26,6 |
17 |
0,21 |
23,45 |
4,98 |
72,47 |
0,21 |
0,30 |
0,08 |
0,12 |
0,03 |
2,78 |
17 |
2,78 |
0,02 |
3 |
26,6 |
32,9 |
18 |
0,23 |
29,75 |
6,69 |
119,61 |
0,17 |
0,22 |
0,07 |
0,09 |
0,02 |
1,57 |
18 |
1,57 |
0,04 |
4 |
32,9 |
39,2 |
8 |
0,10 |
36,05 |
3,61 |
105,27 |
0,28 |
0,34 |
0,11 |
0,13 |
0,02 |
1,82 |
8 |
1,82 |
2,69 |
5 |
39,2 |
45,5 |
6 |
0,08 |
42,35 |
3,18 |
115,09 |
0,31 |
0,37 |
0,12 |
0,14 |
0,02 |
1,81 |
6 |
1,81 |
0,19 |
6 |
45,5 |
60 |
6 |
0,08 |
52,75 |
3,96 |
178,56 |
0,23 |
0,31 |
0,09 |
0,12 |
0,03 |
2,46 |
6 |
2,46 |
0,73 |
Сума |
80 |
1 |
|
27,77 |
634,44 |
|
|
|
|
0,18 |
14,74 |
80 |
14,74 |
103,16 |
||
a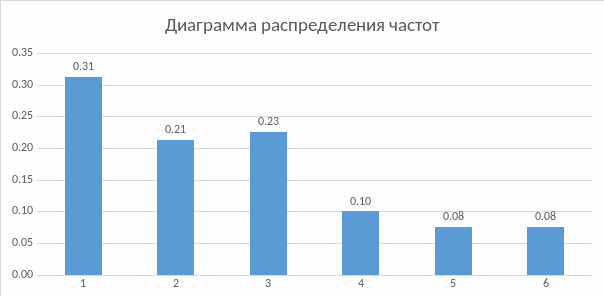
= 27,77
S2 = 634,44
S = 25,19
Задача 2:
2.3 Використовуючи критерій "хі-квадрат" при рівні значущості α = 0,05, перевірити, чи існує залежність між двома незалежними експериментальними вибірками. Для аналізу використовується генеральна сукупність, аналізована в задачі 1. Як незалежні вибірки виділити з генеральної сукупності: групу дівчаток з 1 групи (не заштриховане поле) і групу хлопчиків з 2 групи (заштриховане поле). Використовуючи середні характеристики визначити яка із груп, краще засвоїла теорію.
Т 2.1
Група 1 (дівчата) |
Група 2 (хлопці) |
|||||||||||
28 |
24 |
20 |
48 |
26 |
38 |
20 |
22 |
18 |
28 |
20 |
20 |
|
24 |
20 |
30 |
18 |
30 |
28 |
14 |
22 |
29 |
33 |
40 |
22 |
|
23 |
37 |
42 |
37 |
16 |
46 |
24 |
55 |
|
|
|
|
|
23 |
37 |
28 |
32 |
26 |
19 |
|
|
|
|
|
|
|
Т 2.2
Р.ряд |
|||||||||
Група 1 (дівчата) |
Група 2 (хлопці) |
||||||||
16 |
20 |
24 |
28 |
32 |
38 |
14 |
20 |
24 |
40 |
18 |
23 |
26 |
28 |
37 |
42 |
18 |
22 |
28 |
55 |
19 |
23 |
26 |
30 |
37 |
46 |
20 |
22 |
29 |
|
20 |
24 |
28 |
30 |
37 |
48 |
20 |
22 |
33 |
|
Середнє варіаційного ряду:
=
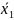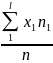= 636/24 = 26,5 – середній варіаційний ряд 1
групи (дівчата)
=
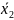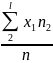= 322/14 = 23 – середній варіаційний ряд 2
групи (хлопці)
Середні ряди незначно відрізняються, можна зробити висновок про те, що рівень засвоєних знань з ТЙМС у першій групі вищий.
Мода варіаційного ряду: 28 – 1 група; 20– 2 група.
Медіана варіаційного ряду: Ме(1) = 28 – 1 група; Ме(2) = 22– 2 група.
Висновок: Використовуючи середні характеристики можна сказати, що 1 група (дівчата) однозначно засвоїли матеріал краще за хлопців із 2 групи.
2021