ЛР3_КОЭД_Шакиров_Ибрагимова_МО417

Министерство науки и высшего образования Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Уфимский государственный авиационный технический университет»

Кафедра вычислительной математики и кибернетики

Лабораторная работа №3

по дисциплине: «Компьютерная обработка экспериментальных данных»

«Метод главных компонент»

Выполнили:

студенты группы МО-417

Шакиров А.Р.

Ибрагимова К.Б.

Проверила:

Харисова Э. А.

Уфа 2022

Цель работы

Практическое освоение метода главных компонент для решения задач снижения размерности.

Порядок выполнения

1. Разработать алгоритм метода главных компонент и программно его реализовать (для проверки правильности вычисления собственных чисел и собственных векторов корреляционной матрицы можно воспользоваться MATLAB).

2. Выполнить анализ экспериментальных данных методом главных компонент.

• Загрузить данные согласно варианту. Отобразите данные на экране монитора в виде таблицы.

• Стандартизовать исходные экспериментальные данные. Построить корреляционную матрицу.

• Удостовериться, что корреляционная матрица значимо отличается от единичной матрицы.

• Рассчитать проекции объектов на главные компоненты.

3. Произвести анализ результатов работы метода главных компонент.

• Проверить равенство сумм выборочных дисперсий исходных признаков и выборочных дисперсий проекций объектов на главные компоненты.

• Построить матрицу ковариации для проекций объектов на главные компоненты.

• Вычислить величину

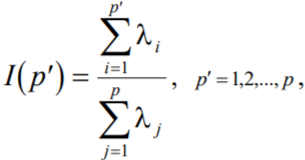
• Причем p - число новых признаков, выбрать минимальным, удовлетворяющим условию I(p’)>0.95.

• Провести анализ и дать содержательную интерпретацию первых двух главных компонент.

Определение главных компонент

Пусть имеется стандартизованная матрица типа «объект – признак»

Векторы-столбцы x¹, x², ..., x^p — это исходные измеряемые признаки.

Главными компонентами называются новые признаки y¹, y²,…, y^p, обладающие свойствами:

1. Главная компонента – это линейная комбинация исходных измеряемых признаков

2. Главные компоненты ортогональны между собой, т.е. некоррелированы cov(yⁱ, y^j)=0,если i≠j.

Главные компоненты упорядочены по мере убывания дисперсии D(y¹)≥D(y²) ≥ … ≥D(y^p) Необходимо определить такое линейное преобразование, задаваемое матрицей С, в результате действия которого исходные данные выражаются набором(матрицей) главных компонент Y = ( y¹,y² ,..., y ^p ), где первые p’ главных компонент обеспечивают требуемую долю дисперсии γ (как правило γ ≥ 0,95).

Задача сводится к определению матрицы С (нахождению неизвестных параметров c_jk j = 1,..., p, k = 1,..., p. Для этого используется аппарат матричной алгебры. Элементы матрицы С рассчитываются на основе корреляционной матрицы R, построенной по входным данным.

Дисперсия j-ой главной компоненты равна j-ому собственному числу λ_j корреляционной матрицы R, (λ1 ≥ λ2 ≥...≥ λp ). Координаты собственного вектора, cоответствующего j-ому собственному числу матрицы R являются искомыми параметрами, c_jk , j = 1,..., p, k = 1,..., p. Сумма выборочных дисперсий исходных признаков равна сумме выборочных дисперсий проекций объектов на главные компоненты.

Несмотря на то, что вместо p признаков получается такое же количество главных компонент, вклад большей части главных компонент в объясняемую дисперсию оказывается небольшим. Исключают из рассмотрения те главные компоненты, вклад

которых мал. При помощи p’ первых (наиболее весомых) главных компонент можно объяснить основную часть суммарной дисперсии в данных.

Относительная доля разброса, приходящаяся на j-ую главную компоненту

Относительная доля разброса, приходящаяся на p’первых компонент

Таким образом, метод главных компонент позволяет описать большой набор признаков p небольшим числом главных компонент p’, при этом различия между объектами зависят от доли изменчивости, связанной с данной главной компонентой. Связи между признаками и главными компонентами – линейные.

Алгоритм метода главных компонент

1. Сформировать матрицу данных

2. Для устранения неоднородности в исходных данных выполнить нормировку (стандартизацию) данных по столбцам где - оценка математического ожидания и среднеквадратическое отклонение по j-ому столбцу (i=1,…,N, j=1,…,p).

3. Построить матрицу ковариации. Ввиду произведенной стандартизации данных матрица ковариации будет корреляционной матрицей исходных данных R порядка pxp.

4. Вычислить собственные числа и собственные векторы корреляционной матрицы, воспользовавшись алгоритмом метода Якоби с преградами (см. Приложение). Упорядочить собственные числа в порядке убывания (λ1 ≥ λ2 ≥...), а также упорядочить собственные векторы 1c ,2c ,..., p c, соответствующие этим собственным числам. В результате получить ковариационную матрицу главных компонент

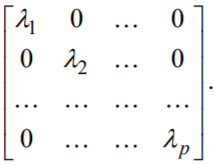
Вычислить матрицу нагрузок на главные компоненты путем нормировки собственных векторов.

5. Рассчитать проекции объектов на главные компоненты

Ход работы

Пусть дана Z — матрица данных согласно варианту 10.

Рисунок 1 – матрица данных Z

Для устранения неоднородности в исходных данных выполним нормировку (стандартизацию) данных по столбцам с помощью функции разработанных, в предыдущих лабораторных работах. Получим матрицу X:

Рисунок 2 – матрица Х

Далее вычисляем матрицу ковариации нормированной матрицы X.

Построим матрицу ковариации с помощью функции разработанных, в предыдущих лабораторных работах. Ввиду произведенной стандартизации данных матрица ковариации будет корреляционной матрицей исходных данных R порядка p x p.

Рисунок 3 – корреляционная матрица R исходных данных Z

Прежде чем начинать анализ главных компонент, проверим гипотезу H₀: корреляционная матрица исходных данных не отличается от единичной матрицы. Если d ≤ χ², то принимаем гипотезу H₀ и применение метода главных компонент нецелесообразно.

sum = 0

for (i in 1:p) {

for (j in 1:p) {

if (i != j) {

sum = sum + R[[i,j]]**2

}

}

}

d = N * sum

chi2 = qchisq(0.95, p*(p-1)/2)

print(d <= chi2)

print(paste("d = ", d))

print(paste("chi2 = ", chi2))

Рисунок 4 – результат проверки гипотезы Н₀

d > χ² при доверительной вероятности = 0.95 и степенями свободы = p(p-1)/2, значит отвергаем гипотезу H₀, т.е. корреляционная матрица значимо отличается от единичной матрицы и применение метода главных компонент является целесообразным.

Вычислим собственные числа и собственные векторы корреляционной матрицы, воспользовавшись алгоритмом метода Якоби с преградами.

Для этого определим функцию отыскания всех собственных значений и собственных векторов симметричной матрицы.

Jacobi <- function(table) {

# точность

eps = 0.0001

N = nrow(table)

A = matrix(NA, nrow = N, ncol = N)

for (i in 1:N) {

for (j in 1:N) {

A[[i,j]] = table[[i,j]]

}

}

# Шаг 1

T = matrix(NA, nrow = N, ncol = N)

for (i in 1:N) {

for (j in 1:N) {

# единичная матрица

T[[i,j]] = if (i==j) 1 else 0

}

}

# Шаг 2

sum = 0

for (j in 1:N) {

for (i in 1:N) {

if (i != j) {

sum = sum + (A[[i,j]]**2)

}

}

}

a0 = sqrt(sum) / N

a_k = a0

continue = TRUE

while(continue) {

# Шаг 3

abs_max_not_diagonal = 0

p = -1

q = -1

for (i in 1:N) {

for (j in 1:N) {

if (i != j && abs(A[[i,j]]) > abs(abs_max_not_diagonal)) {

p = i

q = j

abs_max_not_diagonal = A[[i,j]]

}

}

}

# Шаг 4

if (abs(abs_max_not_diagonal) > a_k) {

y_ = (A[[p,p]] - A[[q,q]]) / 2

x_ = if (y_ == 0) -1

else (-sign(y_) * A[[p,q]] / sqrt(A[[p,q]]**2 + y_**2))

s = x_ / sqrt(2*(1+sqrt(1-x_**2)))

c = sqrt(1-s**2)

for (i in 1:N) {

if (i != p && i != q) {

Z1 = A[[i,p]]

Z2 = A[[i,q]]

A[[q,i]] = Z1*s + Z2*c

A[[i,q]] = A[[q,i]]

A[[i,p]] = Z1*c - Z2*s

A[[p,i]] = A[[i,p]]

}

}

Z5 = s**2

Z6 = c**2

Z7 = s*c

V1 = A[[p,p]]

V2 = A[[p,q]]

V3 = A[[q,q]]

A[[p,p]] = V1*Z6 + V3*Z5 - 2*V2*Z7

A[[q,q]] = V1*Z5 + V3*Z6 + 2*V2*Z7

A[[p,q]] = (V1-V3)*Z7 + V2*(Z6-Z5)

A[[q,p]] = A[[p,q]]

for (i in 1:N){

Z3 = T[[i,p]]

Z4 = T[[i,q]]

T[[i,q]] = Z3*s + Z4*c

T[[i,p]] = Z3*c - Z4*s

}

}

# Шаг 5

continue = FALSE

for (i in 1:N){

for (j in 1:N) {

if (i != j && abs(A[[i,j]]) > eps*a0) {

continue = TRUE

}

}

}

a_k = a_k / (N**2)

}

lambdas = c()

for (i in 1:N) {

lambdas[i] = A[[i,i]]

}

return(list(lambdas, T))

}

Проверим работу функции на тестовом примере.

Рисунок 5 – тестовые данные

test_1 = matrix(

c(1, 0.42, 0.54, 0.66,

0.42, 1, 0.32, 0.44,

0.54, 0.32, 1, 0.22,

0.66, 0.44, 0.22, 1)

, nrow = 4, ncol = 4)

res = Jacobi(test_1)

lambdas = res[[1]]

T = res[[2]]

print(lambdas)

print(T)

Рисунок 6 – вывод тестовых данных

Вычислим собственные числа и собственные векторы корреляционной матрицы

Рисунок 7 – собственные числа и собственные векторы корреляционной матрицы

Упорядочим собственные числа в порядке убывания, а также упорядочим собственные векторы, соответствующие этим собственным числам.

sort_pairs = sort(lambdas, decreasing = TRUE, index.return=TRUE)

C_vect = matrix(NA, nrow=nrow(T), ncol=ncol(T))

for (i in 1:length(lambdas)) {

lambdas[[i]] = sort_pairs$x[[i]]

C_vect[, i] = T[, sort_pairs$ix[[i]] ]

}

print(lambdas)

print(C_vect)

Рисунок 8 – упорядоченные собственные числа и собственные

векторы, соответствующие этим собственным числам

В результате получим ковариационную матрицу главных компонент.

mgk = matrix(NA, nrow=length(lambdas), ncol=length(lambdas))

for(i in 1:length(lambdas)) {

for(j in 1:length(lambdas)) {

mgk[[i,j]] = if (i == j) lambdas[[i]] else 0

}

}

print(mgk)

Рисунок 9 – ковариационная матрица главных компонент

Вычислим матрицу нагрузок на главные компоненты путем нормировки собственных векторов.

mn = matrix(NA, nrow = nrow(C_vect), ncol = ncol(C_vect))

for (i in 1:nrow(C_vect)) {

for (j in 1:ncol(C_vect)) {

mn[[i,j]] = standatization(C_vect, i, j)

}

}

print(mn)

Рисунок 10 – матрица нагрузок на главные компоненты

Рассчитаем проекции объектов на главные компоненты

y = mult_matrix(X, C_vect)

Проверим равенство сумм выборочных дисперсий исходных признаков Х и выборочных дисперсий проекций объектов на главные компоненты у

dispersion_X = dispersion(X)

dispersion_y = dispersion(y)

print(dispersion_X)

print(dispersion_y)

print(sum(dispersion_X))

print(sum(dispersion_y))

Рисунок 11 – проекции объектов на главные компоненты

Суммы выборочных дисперсий равны 10.

Построим матрицу ковариации для проекций объектов на главные компоненты.

Рисунок 12 – матрица ковариации для проекций объектов на главные компоненты

Вычислим величину I(p'), причем p' - число новых признаков. Выбираем p' минимальным, удовлетворяющим условию I(p') > 0.95.

p_1 = 1

for (i in 1:length(lambdas)) {

sum = 0

for (j in 1:i) {

sum = sum + lambdas[j]

}

p_1 = i

part = sum / sum(lambdas)

if (part > 0.95) {

print(p_1)

break

}

}

Рисунок 13 – величина p'

При помощи p'= 7 первых (наиболее весомых) главных компонент можно объяснить основную часть суммарной дисперсии в данных. Вычислим величину I(p') = I(7)

I = sum(lambdas[1:p_1]) / sum(lambdas)

print(I)

Рисунок 14 – величина I(p')

Проведем анализ первых двух главных компонент. Рассмотрим первую главную компоненту. Выведем собственный вектор C1.

Рисунок 15 – собственный вектор C1

Первая главная компонента больше всего зависит от столбцов 1 (Среднеспис. числ. работников, зан. на мал. предпр., тыс.чел.), 2 (Объем произв. по осн. виду деят. продукции мал. предпр. по пром., млн.руб.) и 4 (Объем произв. по осн. виду деят. продукции мал. предпр. по др. отр., млн.руб.).

Рассмотрим вторую главную компоненту. Выведем собственный вектор C2.

Рисунок 16 – собственный вектор C2

Вторая главная компонента больше всего зависит от столбцов 3 (Объем произв. по осн. виду деят. продукции мал. предпр. по с/х, млн.руб.), 7(Объем пром. продукции гос. и мун. формы собств., в %) и 8 (Числ. работников гос. и мун. формы собств., в %).

Вывод

При выполнении лабораторной работы был освоен метод главных компонент для решения задач снижения размерности.