ЛР2_КОЭД_Шакиров_Ибрагимова_МО417

Министерство науки и высшего образования Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Уфимский государственный авиационный технический университет»

Кафедра вычислительной математики и кибернетики

Лабораторная работа №2

по дисциплине: «Компьютерная обработка экспериментальных данных»

«Множественная линейная регрессия»

Выполнили:

студенты группы МО-417

Шакиров А.Р.

Ибрагимова К.Б.

Проверила:

Харисова Э. А.

Уфа 2022

Задание и порядок выполнения работы

Дан вектор y длины N и матрица X размера N x m. Предполагается, что между переменной y и переменными X¹, X², ..., X^m существует линейная зависимость (X¹, X², ..., X^m— столбцы матрицы X):

Найти МНК-оценку вектора коэффициентов линейной множественной регрессии, пользуясь формулой

1. В качестве вектора y взять один из столбцов матрицы Z (из лабораторной работы «Корреляционный анализ»). Тогда остальные столбцы матрицы Z(может быть не все) составят матрицу X.

2. Рассмотреть уравнение регрессии со свободным членом, для этого нужно изменить матрицу Х.

3. Составить программу для нахождения МНК-оценки вектора коэффициентов уравнения линейной множественной регрессии по формуле . Предусмотреть в программе проверку равенства средних значений расчетных и фактических данных зависимых переменных и вычисление коэффициента детерминации.

4. Составить тестовый пример. Для тестового примера взять матрицу размером 5х2 и вектор y длины 5. Выполнить вычисление по формуле вручную.

5. Проверить составленную программу по тестовому примеру и найти МНК оценку для своих исходных данных.

Описание метода

Определение: Уравнение, связывающее один из признаков зависимостью от других признаков, называется уравнением регрессии. Уравнение регрессии зависит от неизвестных параметров.

Классический регрессионный анализ занимается моделями, линейными по параметрам.

Уравнение линейной множественной регрессии:

(*)

это векторное равенство, где вектор независимых переменных, а вектор неизвестных параметров, Ɛ – вектор, играющий роль случайной помехи.

Векторное равенство (*) можно записать в виде:

Здесь Ɛ — случайная компонента, комплексно характеризующая эффект неучтенных признаков.

Введем в рассмотрение матрицу X:

Тогда можем записать уравнение линейной множественной регрессии в матричном виде:

(**)

Постулаты (предположения) регрессионного анализа

Так как в уравнении регрессии фигурируют матрица данных X, вектор неизвестных параметров α и вектор случайной помехи Ɛ, то предположения регрессионного анализа касаются этих трех элементов.

1. На вектор α ограничений не наложено,

2. Ɛ — случайный вектор, следовательно, вектор y – случайный

3. Математическое ожидание всех компонент вектора Ɛ равно нулю:

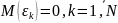
4. Ковариация между Ɛ_k и Ɛ_j:

То есть у различных объектов случайные помехи не коррелированны, а дисперсия вектора Ɛ конечна и одинакова для всех наблюдений (условия проведения наблюдений одинаковы для всех объектов).

5. Матрица X детерминирована (не случайна), то есть значения независимых признаков известны исследователю точно.

6. Ранг матрицы X равен m, то есть в матрице Х имеется m линейно независимых строк или столбцов.

Суть МНК

Суть МНК состоит в следующем: параметры выбираются из условия минимума суммы квадратов отклонений фактических значений от расчетных. Сумму квадратов отклонений фактических значений от расчетных обозначают Q(α)

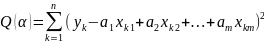
Взяв производную от Q(α) по вектору α и приравняв ее нулю, получили уравнение, из которого выразили α. Пусть α - МНК-оценка вектора α. Тогда

Уравнение регрессии со свободным членом

В силу 3-го постулата регрессионного анализа считается, что эффект неучтенных признаков в среднем равен 0. Это предположение на практике малоправдоподобно. Чаще эффект неучтенных факторов не 0, тогда вместо постулата 3 вводят постулат 3’: .

Тогда уравнение регрессии будет иметь вид:

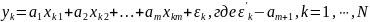
Тогда

Мы оказались в условиях предыдущей системы постулатов, поэтому далее будем считать, что уравнение регрессии имеет вид:

Среднее значение расчетных и фактических данных зависимых переменных

Уравнение регрессии имеет вид: фиктивная переменная.

Вычислим МНК оценку неизвестных параметров:

Тогда , где 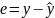, где вектор .

Вектор e называется вектором оценочных отклонений.

МНК оценка удовлетворяет уравнению:

Рассмотрим последнюю строку матрицы 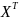. Это единицы ,

Вернемся к равенству просуммируем по k и разделим на N:

Т. е. среднее расчетное значение и средне фактическое значение совпадают.

Коэффициент детерминации

Коэффициент детерминации изменяется в пределах от 0 до 1. Он показывает, как велика доля объясненной дисперсии в общей дисперсии, какая часть общей дисперсии может быть объяснена зависимостью переменной y от переменных x₁, x₂ ,... , x_m.

Ход работы

Дана матрица данных Z размером N×p согласно варианту 10.

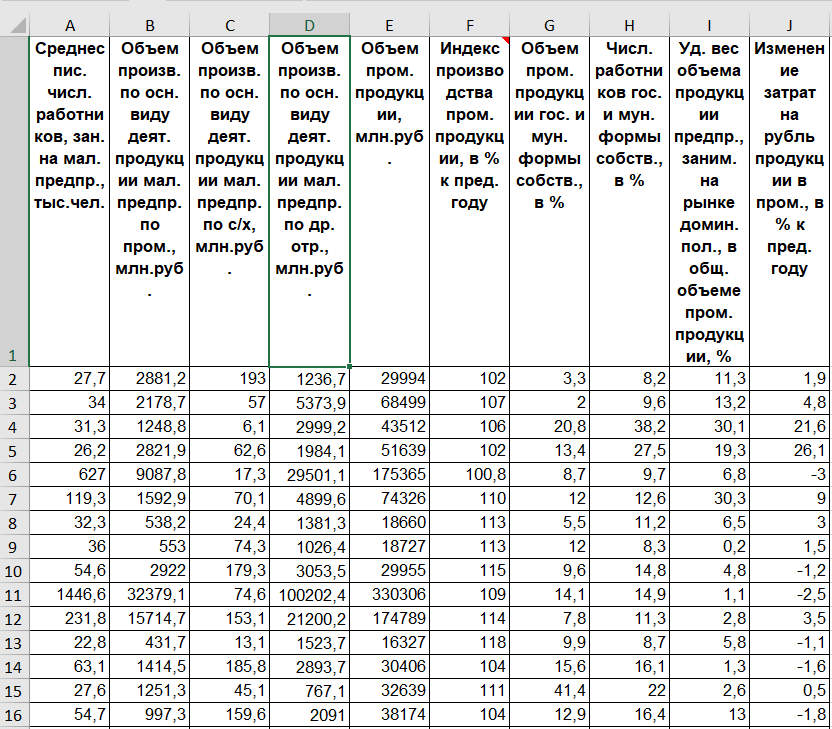
Рисунок 1 – Матрица данных Z

Для выполнения задания разработаем программу в среде разработки RStudio на языке R.

В качестве вектора y берем один из столбцов матрицы Z. Для этого вычислим корреляционную матрицу с помощью функций, разработанных в лабораторной работе №1.

average_columns = average(Z)

dispersion_columns = dispersion(Z)

standatization_matrix = matrix(NA, nrow = N, ncol = p)

for (i in 1:N) {

for (j in 1:p) {

standatization_matrix[[i,j]] = standatization(Z, i, j)

}

}

correlation_matrix = matrix(NA, nrow = p, ncol = p)

for (i in 1:p) {

for (j in 1:p) {

correlation_matrix[[i,j]] = correlation(Z, i, j)

}

}

print(correlation_matrix, digits=2)

Рисунок 2– Корреляционная матрица матрицы данных Z

Выберем такой целевой признак у, чтобы количество признаков с требуемым условием было максимальным. Таким условием является значение модуля коэффициента корреляции между целевым признаком у и некоторым независимым признаком было больше 0.3. Выберем 4-й признак - Объем произв. по осн. виду деят. продукции мал. предпр. по др. отр., млн.руб.

Матрицу зависимых данных X составляют столбцы 1, 2 и 5.

y = Z[, 4]

X = Z[, c(1,2,5)]

В силу 3-го постулата регрессионного анализа считается, что эффект неучтенных признаков E в среднем равен 0. Это предположение на практике малоправдоподобно. Чаще эффект неучтенных факторов не 0, тогда вместо постулата 3 вводят постулат 3', где вместо 0 константа. Пусть данная константа = 1.

Введем в матрицу X столбец неучтенных признаков E, состоящий из единиц.

for (i in 1:N) {

X[[i, "E"]] = 1

}

Вычислим МНК-оценку вектора коэффициентов уравнения линейной множественной регрессии. Для этого определим функции.

Транспонирования матрицы:

transpose <- function(table) {

table_N = nrow(table)

table_p = ncol(table)

result = matrix(NA, nrow = table_p, ncol = table_N)

for (i in 1:table_N) {

for (j in 1:table_p) {

result[[j, i]] = table[[i, j]]

}

}

return(result)

}

X_T = transpose(X)

print(X_T)

Рисунок 3– Транспонированная матрица матрицы Х

Получения минорной матрицы:

get_minor <- function(table, row, column) {

table_N = nrow(table)

table_p = ncol(table)

result = matrix(NA, nrow = table_N - 1, ncol = table_p - 1)

for (i in 1:table_N) {

for (j in 1:table_p) {

if (i != row && j != column) {

row_cur = if(i > row) i - 1 else i;

column_cur = if(j > column) j - 1 else j;

result[[row_cur, column_cur]] = table[[i, j]]

}

}

}

return(result)

}

Вычисления определителя матрицы:

determ <- function(table) {

table_N = nrow(table)

table_p = ncol(table)

if (table_p == 1) {

return(table[[1]])

}

result = 0

for (j in 1:table_p) {

result = result + ((-1)**(j+1) * table[[1, j]] * determ(get_minor(table, 1, j)))

}

return(result)

}

X_det = determ(X)

print(X_det)

Рисунок 4 – Определитель матрицы Х

Умножения матриц:

mult_matrix <- function(a, b) {

a_N = nrow(a)

a_p = ncol(a)

b_N = nrow(b)

b_p = ncol(b)

result = matrix(NA, nrow = a_N, ncol = b_p)

for (i1 in 1:a_N) {

for (j2 in 1:b_p) {

for (i2 in 1:b_N) {

if (is.na(result[[i1, j2]])) {

result[[i1, j2]] = 0

}

result[[i1, j2]] = result[[i1, j2]] + (a[[i1, i2]] * b[[i2, j2]])

}

}

}

return(result)

}

Получения обратной матрицы:

get_reverse <- function(table) {

table_N = nrow(table)

table_p = ncol(table)

det = determ(table)

result = matrix(NA, nrow = table_N, ncol = table_p)

for (i in 1:table_N) {

for (j in 1:table_p) {

adj = (-1)**(i+j) * determ(get_minor(table, i, j))

result[[j, i]] = adj / det

}

}

return(result)

}

Вычислим МНК-оценку вектора коэффициентов уравнения линейной множественной регрессии:

alpha = mult_matrix(mult_matrix(get_reverse(mult_matrix(X_T, X)),X_T), y)

print(format(alpha, scientific=FALSE))

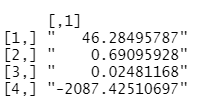
Рисунок 5 – МНК-оценка вектора коэффициентов

уравнения линейной множественной регрессии

Вычислим расчетный столбец y

y_ras = mult_matrix(X, alpha)

print(y_ras)

Рисунок 6 – Расчетный столбец y

Проверим средние значения.

Среднее y расчетное:

print(average(y_ras))

Рисунок 7 – Среднее y расчетное

Среднее y фактическое:

avg_y = average(y)

print(avg_y)

Рисунок 8 – Среднее y фактическое

Средние значения равны.

Вычислим вектор оценочных отклонений e. Для этого определим функцию вычитания матриц и вычислим разность y фактического и расчетного:

sub_matrix <- function(a, b) {

table_N = nrow(a)

table_p = ncol(a)

result = matrix(NA, nrow = table_N, ncol = table_p)

for (i in 1:table_N) {

for (j in 1:table_p) {

result[[i, j]] = a[[i,j]] - b[[i,j]]

}

}

return(result)

}

e = sub_matrix(y, y_ras)

print(e)

Рисунок 9 – Вектор оценочных отклонений e

Вычислим коэффициент детерминации, для этого определим функцию determination_coef:

determination_coef <- function(y, y_ras) {

N = nrow(y)

e = sub_matrix(y, y_ras)

avg = average(y)

sum_e2 = 0

for (i in 1:N) {

sum_e2 = sum_e2 + (e[[i, 1]]**2)

}

sum_otkl = 0

for (i in 1:N) {

sum_otkl = sum_otkl + (y[[i, 1]] - avg)**2

}

R2 = 1 - (sum_e2 / sum_otkl)

return(R2)

}

R2 = determination_coef(y, y_ras)

print(format(R2, scientific=FALSE))

Рисунок 10 – Коэффициент детерминации

Полученный коэффициент детерминации показывает, что доля объясненной дисперсии в общей дисперсии очень велика.

Рисунок 11 – Уравнение регрессии

Составим тестовый пример.

Пусть:

Введем в матрицу X столбец неучтенных признаков E, состоящий из единиц, согласно постулату 3'.

Найдем МНК-оценку вектора коэффициентов линейной множественной регрессии вручную.

Проверим составленную программу по тестовому примеру и найдём МНК оценку для своих исходных данных

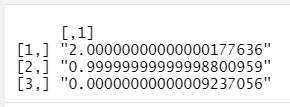
Рисунок 12 – Результат вычисления МНК оценки для тестовых данных

Результат вычисления совпадает со значением, вычисленным вручную.

Рисунок 13 – Уравнение регрессии

Проведем тестирование программы на следующем примере

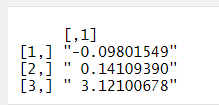
Рисунок 14 – Результат вычисления МНК оценки для тестовых данных

Рисунок 15 – Уравнение регрессии

Вывод

При выполнении лабораторной работы была составлена программа для нахождения МНК-оценки вектора коэффициентов уравнения линейной множественной регрессии по формуле . Была предусмотрена проверка равенства средних значений расчетных и фактических данных зависимых переменных и вычисление коэффициента детерминации.