
МИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра вычислительной техники
Отчет по лабораторной работе №1
по дисциплине «Элементарная база цифровых систем»
Студент гр. |
|
Преподаватель |
Ельчанинов М.Н. |
Тема: ЗНАКОМСТВО С СИСТЕМОЙ ПРОЕКТИРОВАНИЯ QUARTUS II, РЕАЛИЗАЦИЯ КОМБИНАЦИОННОЙ СХЕМЫ Вариант 5
Цель работы – освоение процесса проектирования цифровой схемы в системе автоматизированного проектирования Quartus II, включающего в себя этапы создания цифровой схемы в графическом редакторе, моделирования работы схемы, загрузки результатов проектирования в программируемую логическую интегральную схему и проведение макетного эксперимента. В процессе работы выполняется проектирование простой комбинационной схемы.
Задание - Спроектировать комбинационную схему, реализующую функцию от четырех переменных, заданную набором входных данных, на которых она принимает единичные значения. Необходимо составить таблицу истинности функции, выполнить минимизацию функции с использованием карт Карно или метода Квайна–Мак-Класки, основанного на применении операций склеивания и поглощения.
Компонент x4 входного вектора (x4, x3, x2, x1) следует считать старшим двоичным разрядом.
Необходимо разработать два варианта реализации комбинационной схемы, отличающихся элементным базисом. В первом случае в качестве базиса выбрать примитивы not (НЕ), band* (*-НЕ-И), nand* (*-И-НЕ), а во втором –not (НЕ), bor* (*-НЕ-ИЛИ), nor* (*-ИЛИ-НЕ), где * – количество входов элемента.
Вариант 5: функция 0, 1, 2, 4, 6, 8, 9, 10, 11
Синтез логической схемы
Была составлена таблица истинности, приведенная на рис. 1

Рисунок 1. Таблица истинности
Минимизация функции проводилась с помощью карты Карно, представленной на рис. 2

Рисунок 2. Минимизация картами Карно
Получилась минимизированная функция: y = x1~x2 + ~x2~x3 + ~x1~x4
Перевод в первый базис (И-НЕ, отрицание конъюнкции):
y = ~~(x1~x2 + ~x2~x3 + ~x1~x4)
y = ~(~(x1~x2) * ~(~x2~x3) * ~(~x1~x4))
y = ~((x1|~x2) * (~x2|~x3) * (~x1|~x4))
Перевод во второй базис (ИЛИ-НЕ, отрицание дизъюнкции):
y = ~~(x1~x2 + ~x2~x3 + ~x1~x4)
y = ~(~(x1 * ~x2) * ~(~x2~x3) * ~(~x1~x4))
y = ~((~x1 + x2) * (x2 + x3) * (x1 + x4))
y = ~(~x1 + x2) + ~(x2 + x3) + ~(x1 + x4)
y = ~~((~x1 ↓ x2) + (x2 ↓ x3) + (x1 ↓ x4))
В итоге была разработана схема в Quartus, приведенная на рис. 3

Рисунок 3. Функциональная схема
Результаты функционального моделирования представлены на рис. 4
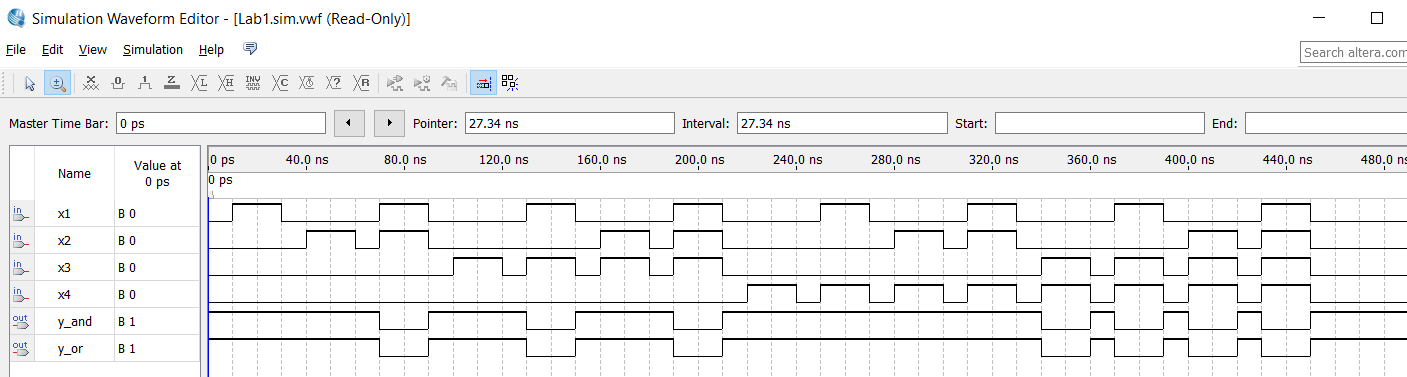
Рисунок 4. Функциональное моделирование
С помощью функционального моделирования можно проверить значение на выходе схемы
Результаты временного моделирования с учетом задержек представлены на рис. 5

Рисунок 5. Временное моделирование
Временное моделирование учитывает временные задержки по
срабатыванию элементов: сигнал на выходе смещен относительно входа, а также существуют помехи
Вывод
В результате выполнения лабораторной работы был освоен процесс
проектирования цифровой схемы в системе автоматизированного
проектирования Quartus II 13. Проработаны этапы: синтез логической схемы,
создание цифровой схемы в графическом редакторе, моделирование работы
схемы.
Санкт-Петербург
2022
