Министерство образования Российской Федерации

Томский политехнический университет

Кафедра теоретической и экспериментальной физики

«УТВЕРЖДАЮ»

Декан ЕНМФ

Определение линейных величин и углов

Методические указания к выполнению лабораторной работы М-00

по курсу «Общая физика» для студентов всех специальностей

Томск-2003

УДК 53.01

Определение линейных величин и углов. Методические указания к выполнению лабораторной работы М-00 по курсу общей физики для студентов всех специальностей. – Томск: Изд - во ТПУ, - 2003. – 12 с.

Составители доцент Н.С. Кравченко,

ст. преп. Н.И. Гаврилина

Рецензент доцент к.ф. - м.н. Ю.А. Сивов

Методические указания рассмотрены и рекомендованы методическим семинаром кафедры теоретической и экспериментальной физики.

20 сентября 2002г.

Зав. кафедрой Ю.Л. Пивоваров

Одобрено учебно-методической комиссией кафедры ТиЭФ.

Председатель учебно-методической комиссии Н.А. Назимова

Ц ель работы: измерение линейных размеров параллелепипеда и цилиндра, определение объёма тел. Оценка погрешности измерений.

Теоретическое содержание

Физические величины определяют свойства тел или характеристики процесса, изменение которых устанавливается количественно, посредством измерений. Точное и правильное измерение физической величины во время наблюдений и опытов составляют главную часть всякого научного исследования в физике. Все физические измерения могут быть произведены с ограниченной точностью. Ограничения точности ставят предел степени подробности информации, полученной из опыта. Только в пределах точности измерений можно сравнить результаты различных опытов.

В различных физических явлениях встречаются различные физические величины, но почти во всех явлениях, кроме прочих, встречаются две величины – длина и время. Длина является мерой протяженности тел, время – мерой длительности процессов и явлений.

Так, измеряя длину отрезка с помощью линейки с миллиметровыми делениями, мы получим измеряемую величину с точностью до миллиметра. С помощью измерительного микроскопа можно значительно повысить точность измерения длины, однако ошибка, хотя и меньшая будет иметь место и в этом случае. Точность измерений физических величин повышается по мере развития техники.

Для измерения физических величин пользуются различными приборами и инструментами. Наиболее простейшие из них: масштабная линейка, штангенциркуль, микрометр, микроскоп. Штангенциркуль, микрометр, микроскоп позволяют сделать измерения более точно. Степень точности определяется устройством инструментов.

Масштабными линейками производят измерение длины. Величина наименьшего деления такой линейки называется ценой одного деления. Обычно цена одного деления равна 1мм.

Если измерение длины производят с точностью до долей миллиметра, то пользуются вспомогательной шкалой измерительного инструмента - нониусом. Нониусы бывают линейными и угловыми.

ЛИНЕЙНЫЙ НОНИУС

Л инейным нониусом называется маленькая линейка с делениями, которая может скользить вдоль большой линейки так же с делениями, называемой масштабом.

Инструмент, имеющий линейный нониус – штангенциркуль.

Рис.1

Штангенциркуль состоит (рис.1) из линейки со шкалой (а) имеющей миллиметровые деления (масштаба) и дополнительной шкалы (b) (нониуса), которая может перемещаться вдоль шкалы.

При измерении длины тела (g) его зажимают между щеками (с) штангенциркуля. Штангенциркулем можно измерять внутренний диаметр отверстий (d) и глубину отверстий (e).

Если нониус имеет 10 делений, которые равны 9 делениям основной шкалы, то каждое деление нониуса короче деления шкалы на 0.1 мм и равно 0.9 мм (рис.2).

При сдвинутых щеках штангенциркуля (с) нулевая отметка нониуса совпадает с нулевой отметкой масштаба, а десятая отметка нониуса – с девятой отметкой масштаба. При этом первое деление нониуса не доходит до первого деления масштаба на 0.1 мм. Второе деление нониуса соответственно не доходит до второго деления масштаба уже на 0.2 мм и т.д.

Следовательно, если раздвинуть щеки штангенциркуля так, чтобы первая отметка нониуса совпадала с первой отметкой масштаба, то между ними образуется просвет 0.1 мм. Если совпадает с отметкой масштаба вторая отметка нониуса, просвет между щеками будет уже 0.2 мм и т. д. Следовательно, отметка нониуса, совпадающая с отметкой масштаба (линейки), указывает расстояние между щеками в десятых долях миллиметра.

В любом положение нониуса относительно масштаба одно из делений нониуса точно совпадает с одним из делений масштаба.

Деления на нониусе наносятся обычно так, что одно деление нониуса составляет делений масштаба, где m – число делений нониуса. Именно это позволяет, пользуясь нониусом, производить отсчеты с точностью до части наименьшего деления масштаба. Пусть расстояние между соседними штрихами масштаба y, а между соседними штрихами нониуса x.

Можно написать, что , откуда получаем .

Величина носит название точности нониуса, она определяет максимальную погрешность нониуса. Пусть L – измеряемый отрезок (длина тела). Для измерения размера тело зажимают между щеками штангенциркуля. Пусть при этом ноль нониуса окажется между k и (k+1) – м делением масштаба. Тогда можно написать , где у - неизвестная пока еще доля k-го деления масштаба. у – отсчитывается по нониусу. Отсчет по нониусу основан на способности глаза, фиксировать совпадение делений нониуса и масштаба.

Так как деления нониуса не равны делениям масштаба, то обязательно найдется на нониусе такое деление n, которое точно совпадает с каким-либо делением масштаба, тогда

у = n x.

Вся длина будет равна или

.

Таким образом, длина отрезка, измеряемого при помощи штангенциркуля, равна числу целых делений масштаба плюс точность нониуса, умноженного на номер деления нониуса, совпадающего точно с некоторым делением масштаба.

Наряду с описанным выше штангенциркулем используют штангенциркули, у которых 10 делений нониуса равны 19 мм. Такая разница сделана только для того, чтобы деления шкалы нониуса были более крупными (удобнее делать отсчет). Точностью нониуса по-прежнему является величина и равна 0,1 мм.

Если нониус штангенциркуля имеет не 10, а 20 делений , то точность его становится равной 0,05 мм.

Правила пользования такими штангенциркулями аналогичные. Отсчет целых делений (мм) производят по шкале линейки до нуля нониуса, затем отсчитывают по нониусу десятые доли миллиметра, число которых равно номеру штриха на нониусе, совпадающему со штрихом масштаба.

Угловой нониус представляет собой дуговую линейку А, укрепленную на штанге, разделенную на градусы и на части градуса; нониус можно перемещать по окружности или полуокружности лимба L (металлического круга или полукруга с делениями, (рис.3). Цена деления шкалы нониуса не равна цене деления шкалы лимба. Допустим, на нониусе нанесено m делений, их общая длина равна (m-1) делений лимба. Если цена деления шкалы нониуса , а цена деления лимба , то ; точность кругового нониуса: .

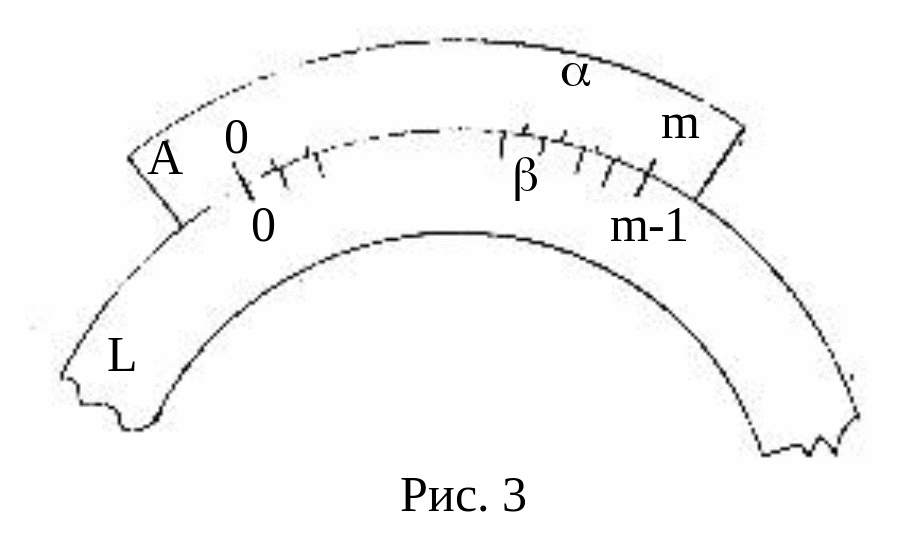
Пусть - измеряемый угол. Ноль нониуса находится между k и (k+1) делениями лимба (рис.4), а деление нониуса n точно совпадает с каким-то делением лимба. То очевидно: . Измеренный угол равен числу целых делений лимба, умноженных на точность лимба k , сложенному с точностью нониуса , умноженной на номер n того деления нониуса, которое точно совпадает с каким-то делением лимба.

Инструмент, имеющий угловой нониус – гониометр. С ним вы будете работать в оптической лаборатории.

Микрометр состоит из двух основных частей: скобы 7 и втулки 3, имеющей с внутренней стороны микрометрическую резьбу, а на поверхности – две шкалы: 3а и 3б одна (выше горизонтальной черты), вторая (ниже горизонтальной черты) (рис.5). Шкала 3б – представляет собой обычную миллиметровую шкалу. Цена деления этой шкалы 1 мм. Каждое деление шкалы 3б разделено пополам и отмечено рисками на шкале 3а. Поэтому цифры проставлены только на шкале 3б. Шкалы 3a и 3б сдвинуты друг относительно друга (рис. 5).

Рис.5

Во втулку (3) ввертывается микрометрический винт (2)). На правый конец винта насажен барабан (5), имеющий шкалу 4. Эта шкала имеет 50 делений. Барабан скреплен с микрометрическим винтом непосредственно или гайкой, навинчиваемой на ее правый конец. При вращении винта она вращается вместе с ним. С правой стороны микрометрического винта ввертывается трещотка (6). Трещотка регулирует нажим на измеряемое тело и ограничивает передвижение винта по втулке. На левом конце скобы находиться упорная щека – наковаленка ( 1).

На барабане (5) имеется шкала (4), имеющая 50 делений. Шаг винта микрометра равен 0,5 мм. При повороте барабана на один полный оборот винт микрометра смещается на 0,5 мм. Это соответствует 1 делению на шкале 3а. Следовательно, цена одного деления шкалы (4) барабана 0.01 мм; при двух оборотах барабана последний проходит 100 делений, и винт отодвигается от щеки на 1мм. Это соответствует 1 мм на шкале 3б.

Для измерения микрометром предмет (д) (рис. 5) помещают между упором 1 и микрометрическим винтом 2. Вращают винт за трещотку 6 до тех пор, пока измеряемый предмет не будет зажат межу упором и концом винта. Момент нажатия фиксируется слабым треском. Отсчет производят по шкалам: миллиметры по линейной шкале (3б), доли миллиметра по шкале (4) на барабане и шкале (3а).

Пусть L- измеряемый отрезок. Предмет зажат между упором и концом винта. Момент нажатия зафиксирован трещоткой.

Для примера различные положения барабана изображены на рис. 6 (а и б).

Рис.6

Случай а: Отсчёт производят следующим образом: по шкале (3б) – 4мм плюс отсчёт по шкале барабана 12 делений, умноженных на цену деления шкалы барабана 0,01 мм. Следовательно, длина L=4 мм+12 0,01мм =4,12 мм.

Случай б: Отсчет по шкале (3б) – 4 мм, отсчет по шкале (3а) – 0,5 мм, отсчет по шкале барабана 12 0,01=0,12мм. Длина L=4+0,5+0,12=4,62мм.

Порядок измерений

1. Измерение линейных размеров параллелепипеда

1. Проверить исправность штангенциркуля. Проверяют исправность штангенциркуля при сдвинутых щеках по совпадению нулевой отметки нониуса с нулевой отметкой шкалы.

2. Штангенциркулем измерить длину, ширину и высоту параллелепипеда и занести в таблицу 1. Замеры произвести 5 раз в различных местах тела.

Таблица 1

№	a (мм)	аi (мм)	ai2 (мм2)	в (мм)	вi (мм)	вi2 (мм2)	с (мм)	ci (мм)	ci2 (мм2)
1
2
3
4
5
среднее значение

3. Найти среднее значение каждой измеряемой величины .

4. Найти объем параллелепипеда

2. Измерение линейных размеров цилиндра

1. Проверить исправность микрометра. Вращаем микрометрический винт за трещотку до первого щелчка. Прибор исправен, если нулевые отметки на шкале 3б и барабане совпадают.

2. Микрометром измерить три раза диаметр и высоту цилиндра и занести в таблицу 2.

Таблица 2

№	D (мм)	Di (мм)	Di2 (мм2)	h (мм)	hi (мм)	hi2 (мм2)
1
2
3
среднее значение

3. Найти среднее арифметическое значение диаметра и высоты .

4. Найти объем цилиндра

Подсчет погрешности

1. Найти среднеквадратичную ошибку среднего арифметического величины по формуле:

2. Найти случайную погрешность величины по формуле:

, где 2,78 – коэффициент Стьюдента для n=5; =0,95.

3. Найти ошибку однократного измерения величины :

, l_a– параметр равномерного распределения для штангенциркуля равен точности нониуса.

4. Найти общую ошибку величины : .

5. Аналогично найти ошибки измерений для ширины и высоты , согласно пунктам 1, 2, 3, 4.

6. Найти относительную и абсолютную ошибки определяемого значения объема параллелепипеда.

, .

7. Округлить до первой значащей цифры, а значение до того разряда, в котором находится эта значащая цифра абсолютной погрешности. Ответ записать в виде: 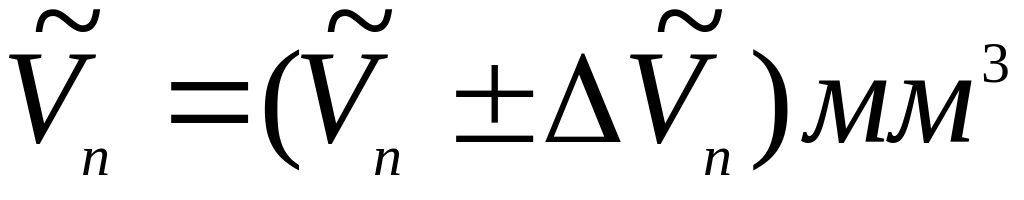с надежностью 0,95.

8. Найти ошибки измерений высоты и диаметра, согласно пунктам 1, 2, 3, 4, учитывая, что для трех измерений коэффициент Стьюдента равен 4,3 и параметр равномерного распределения для микрометра l=0.01 мм равен точности микрометра.

9. Найти относительную и абсолютную ошибки определяемого значения объема цилиндра:

; .

10. Округлить значение и согласно правилам и записать ответ в виде с надежностью 0,95.