Лабораторная работа м-15 Определение отношения удельной теплоемкости газов при постоянном давлении (Ср) к теплоемкости при постоянном объеме (Cv) способом Клемана и Дезорма Теоретическое содержание

Теплоемкостью тела С называется отношение количества тепла , (отученного системой, к приращению ее температуры dT)

(1)

Согласно первому закону термодинамики

(2)

где Q - количество тепла, полученное системой. U - приращение ее внутренней энергии, - величина работы производимой системой.

Величина работы производимой системой равна:

(3)

где р - давление, а V объем системы (газа);

Теплоемкость можно представить как

(4)

Если газ нагревается при постоянном объеме V, внешняя работа. производимая газом, равна нулю и все, сообщаемое ему извне тепло идет целиком на увеличение его внутренней энергии dU. Обозначим теплоемкость газа при постоянном объеме С, она равна по формуле (4)

(5)

При нагревании газа при постоянном давлении Р газ расширяется, сообщаемое ему извне тепло идет не только на увеличение запаса его внутренней энергии dU. но и на совершение работы против сил постоянного внешнего давления. Теплоемкость при этом С_P больше теплоемкости C, на эту работу .

(6)

Удельной теплоемкостью называют величину, численно равную количеству тепла, получаемого единицей массы газа, при нагреве его на 1 К. Непосредственное определение теплоемкости довольно затруднено, особенно Ср. При рассмотрении многих процессов входит отношение этих теплоемкостей, которое мы определили.

(7)

Согласно молекулярно - кинетической теории отношение (7) зависит от числа степеней свободы молекул газа i:

(8)

Для определения k Клеманом и Дезормом был предложен в 1819 году очень простой метод, основанный на адиабатическом расширении или сжатии газа. Адиабатическим процессом называется такой процесс, при котором газ не вступает в тепловой обмен с окружающим пространством. Можно с достаточным приближением рассматривать всякое быстрое изменение объема, как процесс адиабатический, и чем быстрее этот процесс происходит, тем ближе он к адиабатическому.

Стеклянный баллон 1, служащий для опыта, соединен с открытым манометром 2. Накачиваем в него воздух насосом 3 до тех пор, пока разность уровней жидкости в обоих коленах манометра не станет равной 25-30 см. По прошествии 3-5 минут температура воздуха в балоне становится равной температуре окружающей среды.

Рассмотрим часть газа, например, единицу массы, его удельный объем V₁, давление P₁, температура Т₁ (комнатная) (рис.6). Открываем затем быстро закрываем кран 4 на короткое время, соединяем баллон с окружающим воздухом. В результате этого газ переходит в состояние 2 (процесс 1-2).

Так как кран имеет большое сечение к процесс происходит быстро, то в данном случае можно считать адиабатическим. Удельный объем теперь будет V₂. давление P₂ (атмосферное) и температура T₂ В состоянии 2 кран закрываем. Через 3-5 минут воздух нагревается изохорически до комнатной температуры Т₁ и его давление будет P₃ (переход 2-3). Для адиабатического перехода из первого состояния второе справедливо уравнение Пуассона, т.е.

(9)

Сравнивая конечное третье состояние газа с первым состоянием, мы видим, что переход из третьего состояния в первое может быть произведен изотермически. К этому процессу применим закон Бойля - Мариотта, т.е.

(10)

Из уравнений (9) и (10) можно определить k. Для этого возводим уравнение (10) в k степень и делим его на уравнение (9).

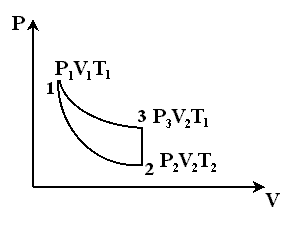
Рис. 6

Рис. 7

(11)

или

(12)

или

(13)

Логарифмируя последнее выражение, находим искомый коэффициент

(14)

Это есть точная формула для коэффициента k. Однако, те условия, в которых производится опыт Клемана и Дезорма, позволяют получить очень простую приближенную формулу.

Обозначим разность уровень жидкости в манометре в первом состоянии через Н, а в третьем состоянии через h. В таком случае

; (15)

где - есть переводной коэффициент для перехода от разностей уровней к давлению.

В обоих случаях второе слагаемое в правых частях мало по сравнению с первым слагаемым. Из (15) получаем и подставляем в (14).

(16)

Величина и много меньше единицы. Для малых значений x справедливо приближенное выражение = . Это равенство получается, если ln (1 - x) разложить в ряд и ограничиться первым членом ряда.)

Тогда:

(17)

или

(18)

По формуле (17) можно производить вычисления k однако величина. Входящая в нее получена в предположении, что кран 4 закрывается в момент окончания адиабатического процесса 1-2 (рис .6).

(17)

или

(18)

По формуле (17) можно производить вычисления k однако величина h, входящая в нее получена в предположении, что кран 4 закрывается в момент адиабатического процесса 1-2 (рис.6).

Е сли экран закрыть до завершения процесса 1-2. т.е. в тот момент, когда давление в баллоне снизятся до некоторой величины но еще не достигнет атмосферного давления Р₂, то как видно из рис. 8 соответствующая разность давлений после осуществления процесса адиабатического расширения и последующего изохорного нагревания определится разность к ординат 2'

Рис. 8

-3' вместо разности ординат 2-З. При этом в состоянии 3 разность уровней жидкости в манометре окажется равной значению h', большему h (h¹) npoпорционально давлению, соответствующему отрезку 3' 2, так как манометр показывает давление воздуха в баллоне по сравнению с атмосферным Р₂). Подготовка в (17-18) завышенного h' вместо h дает завышенное значение величины k по сравнению с действительным.

Е сли кран 4 закрыть спустя некоторое время после завершения процесса 1-2, то за это время температура в баллоне несколько повысится за счет теплообмена с внешней средой (изобарный процесс 2-4, происходящий при давлении, равном атмосферному). В этом случае разность давлений, определяется разностью ординат 4-5 окажется заниженной, а разность уровней жидкости в манометр- h" в состоянии газа 5 окажется меньше h, что приведет к заниженному значению k.

Рис.9

Для получения правильного результата измерения кран 4 установки следует закрыть в тот момент, когда газ накопится в состоянии 2, что практически невозможно. Ввиду этого отрезок ординаты 2-3 приходится определять косвенным путем.

Рассмотрим с этой целью процесс, происходящий в баллоне после открытия крана, предположив, что газ находится в состоянии I (рис. 8). Открыв кран 4, произведем адиабатическое расширение при этом температура газа понизится относительно комнатной до значения Т₂. давление станет равным Р₂ (атмосферному) (процесс 1-2).

Если кран оставить открытым в течении времени после окончания процесса то, температура газа в баллоне за это время несколько повысится за счет теплообмена до величины Т (изобарный процесс 2-4). Закроем кран и дождемся, пока температура газа в баллоне не станет равной температуре окружающей среды Т₁) (изохорный процесс 4-5). При этом давление газа в сосуде повысится на величину Р, которую определим манометром при соответствующей разности уровней , т.к. (индекс у h соответствует значению разности уровней в манометре, когда кран открыт в течение времени ).

Если уменьшить, то величина , как видно из (рис. 8) возрастет, и в пределе, когда (т-4 приблизится к т.2), a к искомому значению h, которое соответствует моменту закрытия крана в состоянии 2. Таким образом величина h, зависит от времени, в течение которого открыт кран 4 или h = f( ) как видно из (рис.8) величина зависит от нелинейно. Однако любой нелинейный процесс с достаточной степенью точности можно аппроксимировать экспонентной. Следовательно можно записать

= (19)

(при ). Логарифмируем выражение (19)

(20)

Получив на опыте ряд значений ln при различных длительностях процесса расширения , можно построить зависимость ln =f( ) (рис. 9) Полученная прямая отсекает на оси ординат отрезок, равный ln h. Потенцируя, найдем искомое значение h. Однако величина h зависит от H. поэтому нужно при построении графика (рис.9) иметь или Н = const. или выразить h в долях H, т.е. взять отношение тогда:

(21)

В этом случае удобнее строить график а не .