Обязательные вопросы к коллоквиуму

1. Физическая реальность и ее моделирование (материальная точка, система координат, система отсчета: базис и градуировка, уравнения движения)

Материальная точка – любая точка пространства, которой прописаны все физические параметры данного тела. Система координат – правило, по которому каждой точке пространства можно поставить в соответствие n, чисел, называемых координатами точки. Система отсчета – совокупность базиса и градуировки. - Базис – множество физических лабораторий (реальных или воображаемых), расположенных во всех точках пространства и снабженных приборами для измерения промежутков времени и отрезков длины. - Градуировка – правило, по которому каждому событию в физическом пространстве, можно поставить в соответствие 4 числа, 3 из которых определяют координаты этого события (задают СК), а четвертое – момент времени, в который это событие произошло. Уравнения движения м.т. – уравнения, описывающие положение радиус вектора относительно выбранной СО в векторном виде или координатной форме.

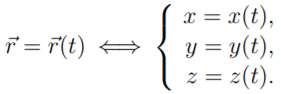
2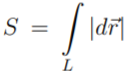 . Кинематические и динамические характеристики движения точки (определения и формулы) Путь – сумма элементарных путей вдоль траектории – длина траектории L – контурный интеграл по траектории

Э лементарный путь – длина вектора элементарного перемещения

Вектор скорости – производная радиус-вектор а по време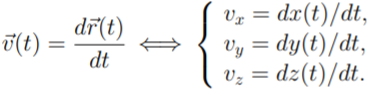ни Величина скорости – модуль(длина) вектора скорости -> производная пути по времени

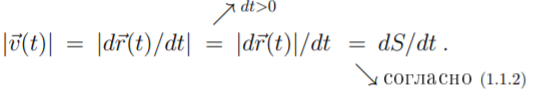
Вектор ускорения – производная вектора скорости по времени

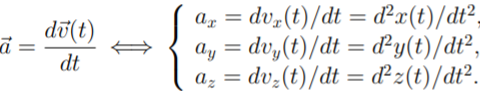
3. Законы Ньютона: 1, 2 и 3 законы Ньютона

1 закон Ньютона: Инерциальные системы отсчета существуют, как математическая абстракция реальных систем отсчета.

2 закон Ньютона: в инерциальных системах отсчета взаимодействие объекта с окружающей средой (сила) вызывает ускорение объекта

3 закон Ньютона: при любом физическом взаимодействии, действие одного тела на другое вызывает равное по величине и противоположно направленное действие второго тела на первое. Нельзя записать в векторной форме, т.к. вектора приложены к разным точкам пространства.

4. Теоремы о движении центра масс (+ внутренние и внешние силы)

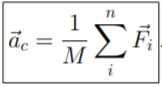При любых взаимодействиях каждой из частиц механической системы с окружающей средой, центр масс системы движется таким образом, как будто все силы, действующие на отдельные частицы системы, приложены к одной точке – центру масс.

А налитическая форма теоремы: ,т.к. – сила, действ на частицу.

Силы, действующие на каждую точку системы:

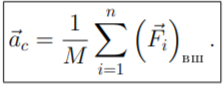- Внутренние силы – силы, со стороны всех остальных частиц - Внешние силы – действующие на частицу со стороны других тел, не входящих в рассматриваемую систему Но по 3 з.Н. при суммировании все вектора внутренних сил попарно обнуляются. Тогда Т. о движении центра масс принимает вид: Если система находится во внешнем стационарном однородном поле, то никакими действиями внутри системы невозможно изменить движение центра масс системы.

5. Движение тела с переменной массой (уравнение Мещерского)

П усть за бесконечно малое время dt масса системы изменилась на бесконечно малую dm Если скорость u вылетевшей частицы dm отн. Системы не равна 0, тогда по ЗСИ импульс системы изменится (скорость увеличится на dv) Но по Т. о движении центра масс, импульс системы может измениться под действием внешней силы

Тогда полное изменение импульса системы за время dt:

П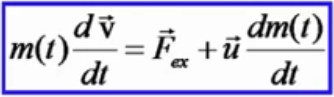 олучаем уравнение Мещерского:

6. Описание движения твердого тела: моменты силы, импульса и инерции (определения и формулы для твердого тела и точки)

М омент импульса точки: вектор, равный векторному произведению радиус-вектора рассматриваемой материальном точки на импульс

Момент импульса абсолютно твердого тела относительно оси вращения равен произведению его момента инерции оЁтносительно той же оси на угловую скорость.

М омент силы м.т. отн. произвольной С.О. – векторное произведение радиус вектора м.т. на вектор силы

Момент силы твердого тела – произведение прилагаемой силы на плечо силы

Момент инерции точки – произведение массы точки на квадрат расстояния до оси вращения.

Момент инерции абсолютно твердого тела отн. оси – сумма произведений массы каждой точки твердого тела на квадрат расстояния до оси вращения тела.

7. Работа силы на произвольном перемещении (формула)

Работа силы на произвольной траектории L равна ,где L – контурный интеграл (и. вдоль траектории)

8. Потенциальные поля: определение (аналитическое – формула и формулировка)

Потенциальное силовое поле – силовое поле, в котором возможно введение потенциальной функции(некоторая скалярная функция координат), то есть удовлетворяющее условию:

9. Закон сохранения энергии (в наиболее общей форме и частные случаи - определения)

Закон сохранения полной механической энергии (ЗСПМЭ) – полная механическая энергия тела сохраняется в любых состояниях этого тела, если в этих состояния работа не потенциальных сил над телом равна 0. (кинетическая с потенциальной изменяются)

Частные случаи – - при движении тела в потенциальном поле его полная механическая энергия сохраняется (полное отсутствие не потенциальных сил) - в замкнутых системах (при полном отсутствии сил, либо когда их сумма = 0), полная механическая энергия сохраняется

10. Удар частиц (типы и определения)

Абсолютно неупругий удар – удар, после которого частицы движутся как единое целое. (ЗСПМЭ не выполняется)

Абсолютно упругий удар – удар, при котором частицы движутся с различными скоростями и выполняются законы сохранения энергии и импульса. Делится на: - Нецентральный – удар, после которого частицы разлетаются в направлениях, не совпадающих с направлением их первоначального движения, он моделирует удар шаров, движущихся по прямой, не совпадающей с линией, соединяющей центры их масс. - Центральный – удар точечных частиц, моделирующий удар шаров, двигавшихся вдоль линии, соединяющей центры их масс.

11. Принцип эквивалентности

Гравитационная и инертная массы тела численно всегда совпадают

12. Исходные постулаты СТО (основной постулат СТО, дополнительный постулат СТО)

Основной постулат СТО – скорость света не зависит от выбора ИСО, во всех ИСО одинакова. Дополнительный постулат СТО – время и пространство изотропны и однородны

13. Синхронизация часов в СТО

1) Выбираем базовые часы и устанавливаем на них показания времени t0 2) Измеряем расстояния до остальных часов li и устанавливаем на них показания времени t0i = t0 + li/c 3) В момент t0 запускаем базовые часы и одновременно посылаем сигнал со скоростью света на все остальные часы, в момент, когда сигнал достигает часов, они запускаются

14. Относительность понятия одновременности.

События, происходящие в разных точках, одновременные в одной ИСО, во всех остальных ИСО не одновременны.