2 сем / К экзамену 35, 36, 37

3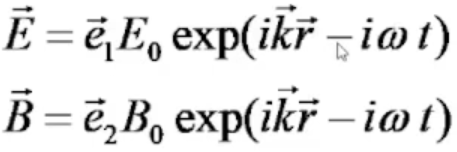 5. Плоские волны

Электрическая и Магнитная плоские волны

Е сли частота волны постоянна – волны монохроматические

В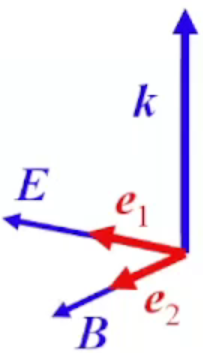 олновое уравнение устанавливает условие связи для констант: |k| - волновое число

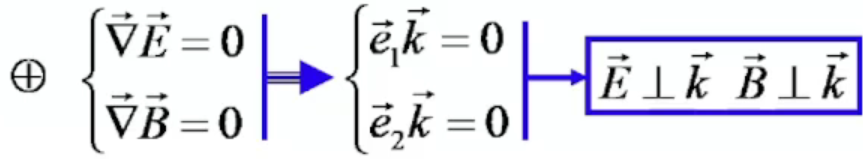
Доказательство под цифрой 1. Волновому вектору(вдоль которого распространяется волна) перпендикулярны вектора напряженности электрического и магнитного поля и направлены они вдоль единичных векторов поляризации.

Закон Фарадея выражается через характеристики электромагнитной волны(Фурье?) Все три вектора взаимно перпендикулярны. Доказательство под цифрой 2.

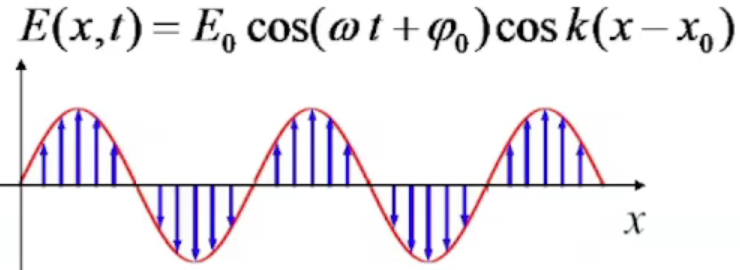
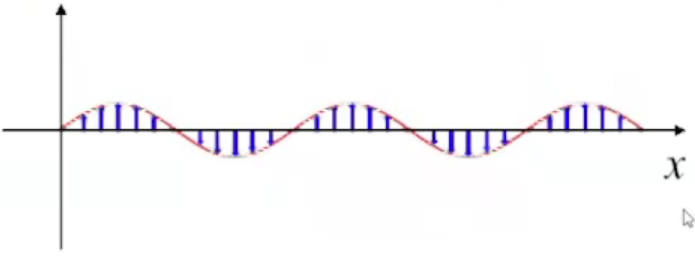
Синусоидальные стоячие волны Крутится вокруг оси Х

Э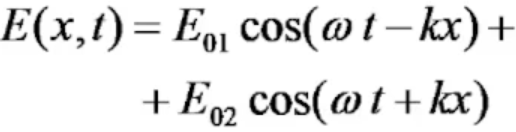 то не значит, что она именно так, это просто удобный способ её изучения(???)

Синусоидальные волны, распространяющиеся вдоль оси Х Бежит вдоль оси Х, но не крутится.

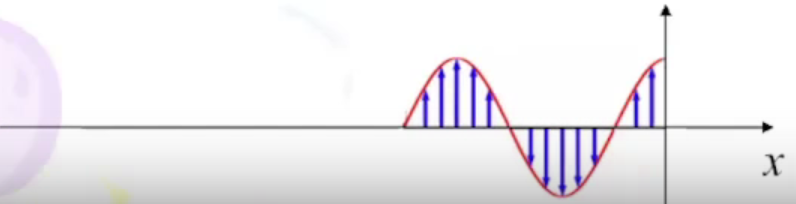
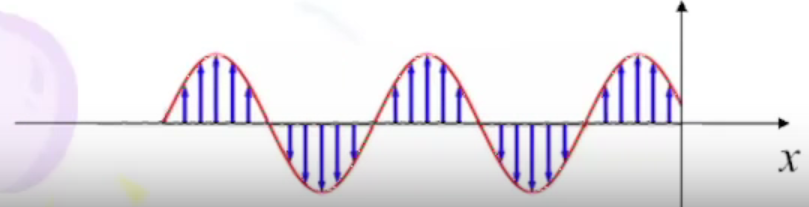
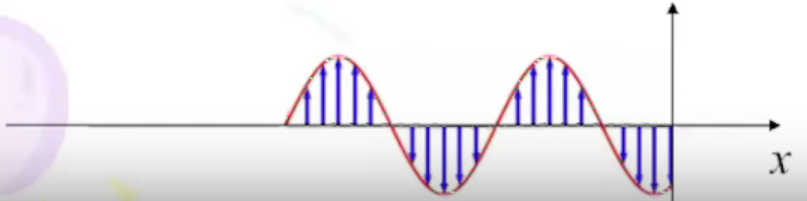
36. Суперпозиция плоских волн (эллиптическая поляризация)

Теорема о суперпозиции решений – однородному линейному дифференциальному уравнению удовлетворяет любая линейная комбинация его решений.

Суперпозиция – просто линейная комбинация каких-то решений уравнений Максвелла, если создать физ. условия, то они могут складываться между собой

Л юбую сумму плоских волн можно получить с помощью Фурье преобразований по принципу суперпозиции.)

3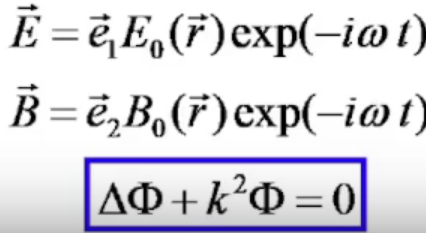 7. Частные решения волновых уравнений (двухмерный и трехмерный случаи)

Волновые уравнения допускают частные решения вида:

Н о Е0 и В0 – это уже не константа, а функция координат, тогда если их подставить в уравнение Максвелла и взять все производные , зависимость от времени exp( ) сократиться и мы получим уравнение:

Где Ф – это величина либо для электрического, либо для магнитного поля

П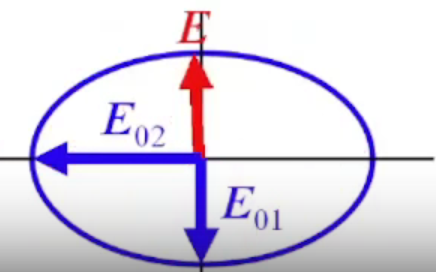 лоскую монохроматическую волну всегда можно представить в виде суммы двух других независимых плоских монохроматических волн, волновые вектора которых взаимно перпендикулярны.

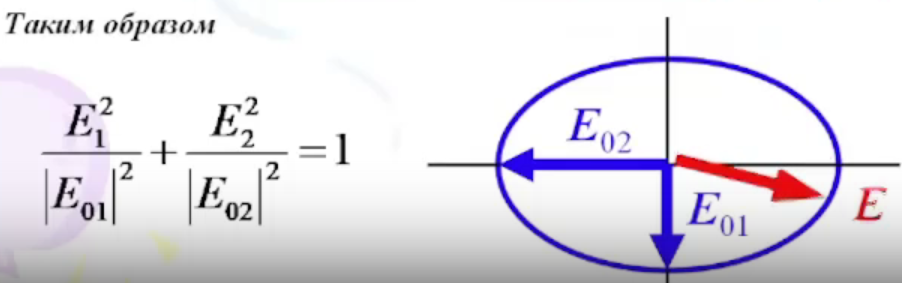
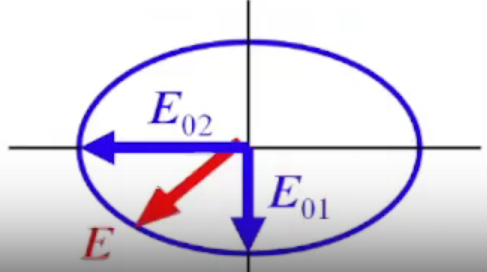
Е - крутится

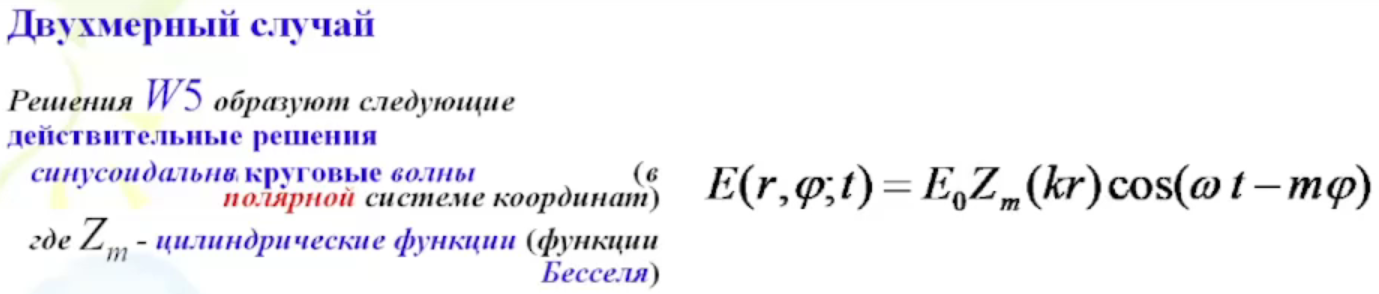
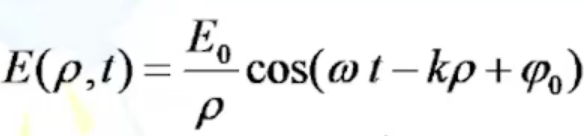
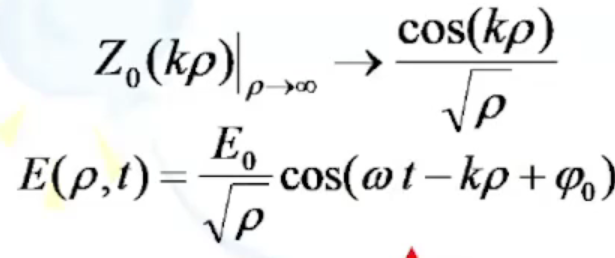
1 . Доказательство к первому

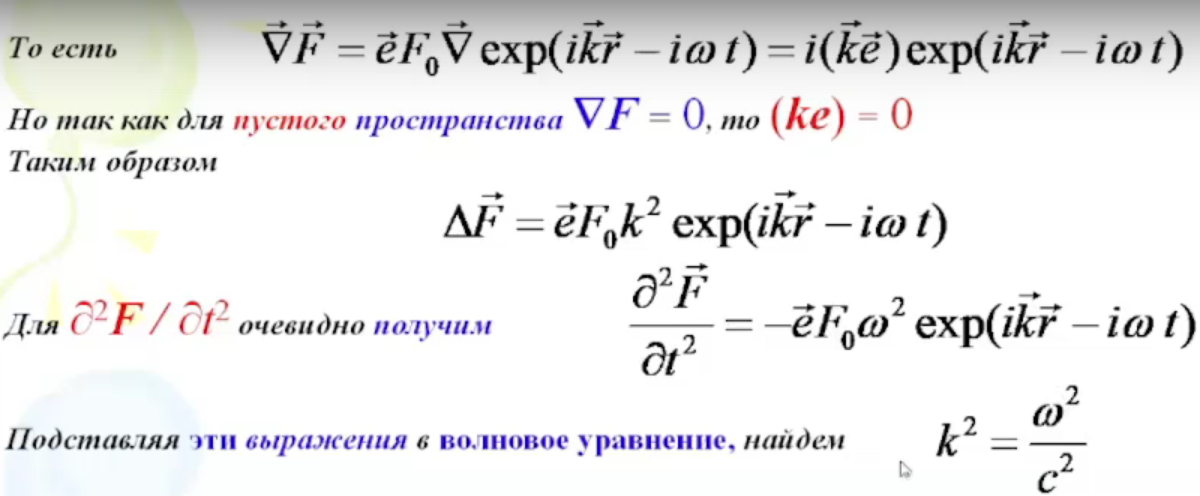
2. Доказательство к первому