Лабораторная работа № 6 Вычисление функций с использованием их разложения в степенной ряд

Цель: закрепление навыков в организации итерационных и арифметических циклов, использования вспомогательных алгоритмов (функций с передачей параметров по значению).

1.1. Краткие теоретические сведения

Выражение вида называется числовым рядом. Ряд называется сходящимся, если частичные суммы ряда стремятся к некоторому числу S. Примером сходящегося числового ряда является сумма бесконечно убывающей геометрической прогрессии. Сумму числового ряда можно найти с любой наперёд заданной точностью, если прибавлять слагаемые до тех пор, пока они не станут меньше заданной точности.

Выражение вида называется степенным рядом. Большинство элементарных математических функций раскладываются в степенные ряды внутри некоторого интервала. Именно с помощью разложения в степенной ряд происходит вычисление этих функций на компьютере. Сумму степенного ряда в каждой точке интервала сходимости можно найти с любой наперёд заданной точностью, если прибавлять слагаемые до тех пор, пока они не станут меньше заданной точности.

Выражение вида называется функциональным рядом. Функциональные ряды также сходятся внутри некоторого интервала и его сумму можно вычислить, прибавляя очередное слагаемое, так же, как и для степенного ряда.

Обычно формула общего члена суммы принадлежит одному из следующих трех типов:

а) ; ; ;

б) ; ; ;

в) ; ; .

В случае а) для вычисления члена суммы z_n целесообразно использовать рекуррентные соотношения, т. е. выражать последующий член суммы через предыдущий: z_n+1=(x, n)·z_n. Это позволит существенно сократить объем вычислительной работы. Кроме того, вычисление члена суммы по общей формуле в ряде случаев невозможно (например из-за наличия n!).

В случае б) применение рекуррентных соотношений нецелесообразно. Вычисления будут наиболее эффективными, если каждый член суммы вычислять по общей формуле z_n=(x, n).

В случае в) член суммы целесообразно представить в виде двух сомножителей, один из которых вычисляется по рекуррентному соотношению, а другой непосредственно z_n=(x, n)*с_n(x,n), где с_n=c_n-1(x,n).

1.2. Постановка задачи

Для х, изменяющегося от a до b (интервал [a ; b] целиком лежит внутри интервала, указанного в третьей колонке) с шагом , вычислить функцию y=f(x), используя ее разложение в степенной ряд (вторая колонка) в двух случаях:

а) для заданного количества слагаемых N (величина зависит от свойств степенного ряда, примерное значение N указано в четвёртой колонке);

б) для заданной точности  (близкое к нулю положительное число, например, 0.1, 0.01, 0.001, 0.0001).

Числа N, , a и b ввести с клавиатуры и проверить на корректность.

Для сравнения найти точное значение функции, указанное в пятой колонке.

Результаты расчетов вывести на экран в виде таблицы (рамка не обязательна):

N п/п	x	Sn	Se	S
1
2
. . .	. . .	. . .	. . .	. . .
10

Здесь x  значение параметра; Sn  значение суммы для заданного n; Se  значение суммы для заданной точности; S точное значение функции.

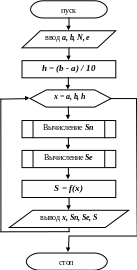
Примерная блок-схема (защита от дурака не показана)

1.3. Варианты заданий

№	Разложение в ряд функции f(x)	диапазон изменения аргумента	N	Функция f(x) сумма ряда (для проверки)
			40
			10
			40
			20
			40
			10
			40
			20
			10
			10
			25
			35
			10
			10
			15

1.4. Методические указания

1. Алгоритм решения задачи сводится к трем циклам, причем два из них вложены в третий. Внешний цикл организует изменение параметра х. Внутренние циклы суммируют слагаемые при фиксированном параметре x (первый цикл  арифметический для заданного n, второй  итерационный для заданной точности ). При организации этих циклов следует обратить внимание на правильный выбор способа вычисления очередного слагаемого z_n (в зависимости от его вида) и правильное присвоение начальных значений переменным цикла.

2. Написать программу для решения задачи с использованием функций. В основной программе внутри цикла по переменной x вызываются поочередно функции для вычисления Sn (зависит от параметров x и N), Se (зависит от параметров x и e), и S (зависит от параметра x), а затем на экран выводятся полученные значения.

1.5. Критерии оценивания работы

В таблице приведены критерии, по которым студент может оценить свою работу.

Критерии оценивания заданий	Процент
При наличии синтаксических ошибок (программа не транслируется) работа не оценивается (0 процентов выполнения)	(набранные баллы)*0
Результаты работы всех трёх программ совпадают на одинаковых входных данных. При N, большем или равном указанному в таблице вариантов, SnSeS, причём |Se-S|e . Расхождение в результатах вычислений говорит о наличии логических ошибок.	-50%
Работающая программа 1 (вложенные циклы, функции пользователя отсутствуют)	30
Работающая программа 2 (три пользовательских функции)	30
Итого -	Шестьдесят баллов
Дополнительно к этому общая оценка работы:
Вычисления организованы рациональным способом, в частности, степени величин при суммировании ряда вычисляются накоплением, а не использованием функции возведения в степень; величины, не изменяющиеся в теле цикла, вынесены за пределы тела цикла.	10
Аккуратное форматирование, комментариев необходимое и достаточное количество.	5
Программа выводит сведения о разработчике и номер варианта	5
Ввод данных организован таким образом, чтобы свести к минимуму ошибки при вводе, организована защита от дурака	10
Вывод данных на экран соответствует заданию	10
Итого	100 %