
Дискретка / diskretochka (1)
.pdf
От противного: пусть  и граф не связный.
и граф не связный.
Рассмотрим граф  , где
, где  – произвольная компонента, а
– произвольная компонента, а  - все вершины из графа, не входящие в
- все вершины из графа, не входящие в  .
.
Пусть  имеет
имеет  вершин, возможны 3 случая:
вершин, возможны 3 случая:
1) , тогда в |
вершин. |
2) , тогда в |
вершина. |
3) , тогда в |
вершин. |
Покажем, что во все 3 случая противоречивы.
1)Число ребер с  ребрами не превосходит числа ребер в графе с тем же
ребрами не превосходит числа ребер в графе с тем же
количеством вершин. |
. |
2)Аналогично. |
|
32.Необходимое и достаточное условие неразделимости связного графа.
Точка сочленения – вершина графа, при удалении которой увеличивается число компонентов связности.
Неразделимый граф – граф, не имеющий точек сочленения.
Теорема. Критерий неразделимости графа.
Граф с числом вершин >3 неразделим , когда любые его вершины принадлежат некоторому циклу.
Доказательство. Без доказательства.
33.Планарность. Дерево, плоское изображение дерева.
Плоское изображение графа – изображение, в котором ребра графа не пересекаются. Планарный граф – граф, имеющий плоское изображение.
Дерево – связный граф без циклов.
Покрывающее дерево -  , где
, где  .
.
Наименьшее покрывающее дерево – покрывающее дерево, имеющее наименьший вес.
Плоское изображение дерева.
Пусть  – дерево,
– дерево,  – корень дерева.
– корень дерева.
Посчитаем расстояние от  до любой другой вершины.
до любой другой вершины.
 – max длина цепи.
– max длина цепи.
Проводим  горизонтальных линий.
горизонтальных линий.
На 1-ой горизонтали расположим все вершины, удаленные от корня на 1. На 2-ой горизонтали расположим все вершины, смежные с вершинами: ,…,
,…, И так далее.
И так далее.
Начиная от корня, соединяем линиями смежные между собой вершины, получаем плоское изображение дерева.
34.Необходимое и достаточное условие для того, чтобы граф был деревом.
Теорема. Критерий того, что граф является деревом.
Граф является деревом , когда выполняется любое из 3 условий:
1)любые 2 вершины соединены единственной цепью.
2)граф  связный, число вершин равно n=m+1.
связный, число вершин равно n=m+1.
3)граф  не содержит циклов, n=m+1.
не содержит циклов, n=m+1.
Доказательство.
Необходимость. Граф  является деревом.
является деревом.
1)От противного: найдутся 2 вершины, соединенные 2-мя цепями:  одна цепь. Тогда существует цикл – противоречие.
одна цепь. Тогда существует цикл – противоречие.
2)По индукции: для  и
и  справедливо.
справедливо.
Предположим, что формула справедлива для дерева с  вершинами. При удалении любого ребра, получим 2 компоненты связности.
вершинами. При удалении любого ребра, получим 2 компоненты связности.
 вершин в одной компоненте связности,
вершин в одной компоненте связности,  вершин в другой. Число ребер в первой компоненте связности:
вершин в другой. Число ребер в первой компоненте связности:  .
.
Число ребер во второй компоненте связности:  . Тогда число ребер в исходном дереве:
. Тогда число ребер в исходном дереве:
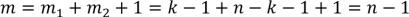 , где крайняя единица в начале равенства – удаленное ребро.
, где крайняя единица в начале равенства – удаленное ребро.
3)Доказано через 2-е. Достаточность.
1)Любые 2 вершины соединены единственной цепью, значит граф связный.
От противного: 2 вершины, соединены 2-мя цепями, существует цикл – противоречие. 2)Граф  связный и число вершин n=m+1.
связный и число вершин n=m+1.
От противного: предположим, что в  есть циклы, удалим все висячие вершины (со степенью 1)
есть циклы, удалим все висячие вершины (со степенью 1)

 , удалим все висячие вершины: получим граф
, удалим все висячие вершины: получим граф 
 Так до тех пор, пока не останется висячих вершин.
Так до тех пор, пока не останется висячих вершин.

 (! – штрих) степень каждой вершины
(! – штрих) степень каждой вершины  . По лемме о рукопожатии:
. По лемме о рукопожатии:
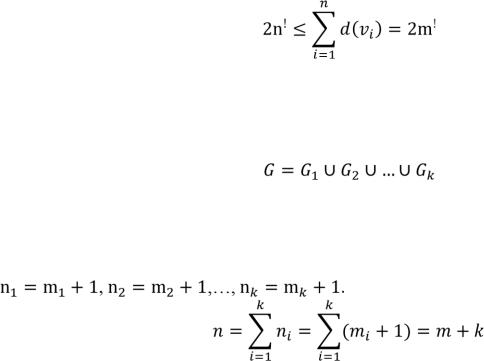
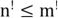 – противоречие, так как
– противоречие, так как 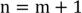 .
.
3) не содержит циклов,
не содержит циклов,  . Надо доказать, что
. Надо доказать, что  – дерево.
– дерево.
От противного:  - не связный граф. Пусть он состоит из
- не связный граф. Пусть он состоит из  компонентов связности, тогда граф:
компонентов связности, тогда граф:
, где 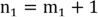 ,
,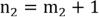 ,…,
,…, .
.
Каждая компонента связности представляет связный граф без циклов, тогда
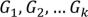 – это деревья. Посчитаем число вершин в этих деревьях. Если граф – дерево, то
– это деревья. Посчитаем число вершин в этих деревьях. Если граф – дерево, то  .
.
 – противоречие, так как
– противоречие, так как  , значит
, значит  – дерево.
– дерево.
35.Формула Эйлера. Следствия из формулы Эйлера.
Грань – область графа, ограниченная ребрами.
Плоское изображение графа – изображение, в котором ребра графа не пересекаются. Планарный граф – граф, имеющий плоское изображение.
Формула Эйлера. Для плоского изображения связного планарного графа справедлива формула: n-m+r=2, где r- количество граней, n – число вершин, m – число ребер.
Доказательство.
Пусть  – планарный граф с плоским изображением. Возможны 2 случая. 1)
– планарный граф с плоским изображением. Возможны 2 случая. 1) – дерево,
– дерево, 
 .
.
2) не является деревом. Тогда в нем есть циклы. Удалим любое ребро цикла. Число ребер и граней уменьшится на 1.
не является деревом. Тогда в нем есть циклы. Удалим любое ребро цикла. Число ребер и граней уменьшится на 1.
Тогда граф 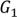
 . Удаляем ребра в циклах, пока их не останется.
. Удаляем ребра в циклах, пока их не останется.
Получим граф 
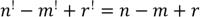 , так как в графе нет циклов
, так как в графе нет циклов 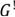 является деревом
является деревом  .
.
Плоский граф – граф, заданный плоским изображением.
Триангуляцией называется плоский граф, все грани которого – треугольники. Максимальный плоский граф – плоский граф, в котором, при добавлении в этот граф ребра, перестает быть плоским. Максимальный плоский граф является триангуляцией.
Следствия из формулы Эйлера.
1)Если в плоском графе каждая грань – k-элементный цикл (каждая грань ограничена k ребрами), то число ребер  .
.
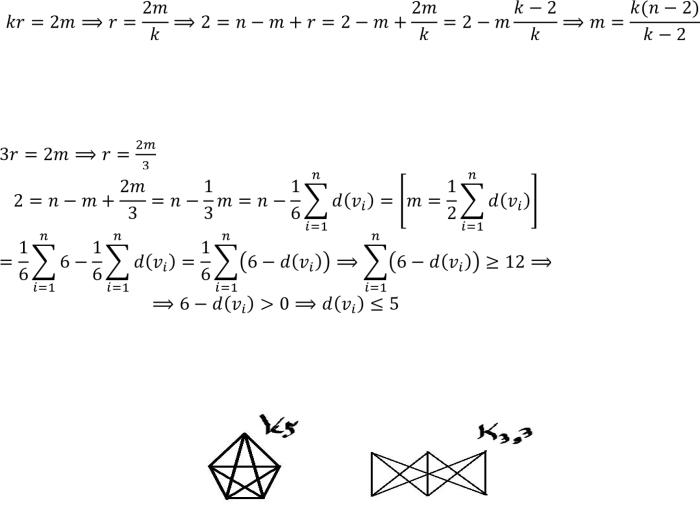
2)В каждой триангуляции число ребер  .
.
3)Необходимое условие планарности.
В планарном графе с числом вершин n≥3, число ребер 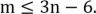
4) В каждой триангуляции найдется вершина, степень которой 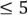 .
.
36.Необходимое и достаточное условие планарности графа.
Граф, получающийся из  добавлением вершин на ребрах не в местах их пересечения, называется графом типа I.
добавлением вершин на ребрах не в местах их пересечения, называется графом типа I.
Граф, получающийся из  добавлением вершин на ребрах не в местах их пересечения, называется графом типа II.
добавлением вершин на ребрах не в местах их пересечения, называется графом типа II.
Теорема. Критерий планарности графа (Понтрягина-Куратовского).
Граф планарен , когда не содержит частей, изоморфных графам типа I или типа II.
Доказательство.
Необходимость.
От противного: граф содержит изоморфизм к графам типа I или типа II. Тогда  и
и 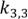
– полные планарные графы.
Вграфе 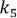 :
: 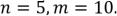 По следствию 2 (из Эйлера)
По следствию 2 (из Эйлера)  – противоречие.
– противоречие.
Вграфе  :
: 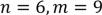 . По формуле Эйлера:
. По формуле Эйлера: 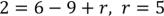 . Оценим число ребер.
. Оценим число ребер.
Каждое ребро не принадлежит 3-х элементному циклу, но принадлежит 4-х элементному.

 – противоречие, так как
– противоречие, так как  .
.
37.Эйлеров граф. Необходимое и достаточное условие для того, чтобы граф был Эйлеровым.
Если в графе  ребер, то путь не может быть
ребер, то путь не может быть 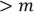
Эйлеров путь – путь длины  .
.
Эйлеров граф – граф, содержащий циклический Эйлеров путь.
Теорема. Критерий эйлеровости графа.
Связный граф является Эйлеровым , когда все его вершины четные.
Доказательство.
Необходимость.
Пусть связной граф  является Эйлеровым, тогда существует циклический Эйлеров путь. Выберем любую вершину графа. Число ребер входа равно числу ребер выхода. Любая промежуточная вершина Эйлерова пути четная.
является Эйлеровым, тогда существует циклический Эйлеров путь. Выберем любую вершину графа. Число ребер входа равно числу ребер выхода. Любая промежуточная вершина Эйлерова пути четная.
Достаточность.
Пусть степени всех вершин – четные. Докажем, что существует циклический Эйлеров путь. Выберем любую вершину  , двигаясь по ребрам, окрашиваем их. Продолжим движение по неокрашенным, вернемся в
, двигаясь по ребрам, окрашиваем их. Продолжим движение по неокрашенным, вернемся в 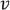 . Получим циклический путь, который состоит из окрашенных ребер. (
. Получим циклический путь, который состоит из окрашенных ребер. ( ) 1 случай: все ребра окрашены.
) 1 случай: все ребра окрашены.
2 случай: есть хотя-бы одно неокрашенное ребро. Поскольку граф связный, то найдется ребро, один конец которого принадлежит окрашенному ребру.
Пусть у 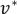 степень четная, тогда путь может закончиться в вершине
степень четная, тогда путь может закончиться в вершине 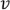 .
.

 , где
, где  – некоторая цепь. Получили другой циклический путь. Если остались еще неокрашенные ребра, то продолжаем процедуру. Получаем Эйлеров путь.
– некоторая цепь. Получили другой циклический путь. Если остались еще неокрашенные ребра, то продолжаем процедуру. Получаем Эйлеров путь.
38.Необходимое и достаточное условие существования Эйлерова пути.
Теорема. Критерий существования Эйлерова пути.
В связном графе существует Эйлеров путь, соединяющий 2 разные вершины , когда эти вершины являются единственными нечетными вершинами в графе.
Доказательство.
В графе  и
и  – единственные нечетные вершины в графе
– единственные нечетные вершины в графе  . Покажем, что существует Эйлеров путь. Возможны 2 случая. 1)Вершины
. Покажем, что существует Эйлеров путь. Возможны 2 случая. 1)Вершины и
и 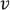 соединены ребром.
соединены ребром.
Получили новый граф, путем зачеркивания единственного ребра, степени всех вершин
– четные. 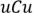 а) Граф не распался на 2 компоненты связности. По предыдущей теореме, существует
а) Граф не распался на 2 компоненты связности. По предыдущей теореме, существует
Эйлеров путь, добавляя назад ребра, получим:
 .
.
б) Граф распался на 2 компоненты связности. Степени всех вершин четные, значит в каждой компоненте связности существует циклический Эйлеров путь.  – в одной компоненте связности.
– в одной компоненте связности.
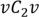 – в другой компоненте связности.
– в другой компоненте связности.
Тогда получаем:  2)Вершины
2)Вершины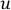 и
и  не соединены ребром.
не соединены ребром.
Добавляем ребро, степени вершин – четные, значит, существует циклический Эйлеров путь. ( )
)
Удаляем ребро, получаем:  . Получили Эйлеров путь.
. Получили Эйлеров путь.
39.Гамильтонов граф. Достаточное условие гамильтоновости графа.
Гамильтонов цикл – простой путь длины  .
.
Цепь (нециклический простой путь) может иметь  ребер. Гамильтонов граф – граф, содержащий гамильтонов цикл.
ребер. Гамильтонов граф – граф, содержащий гамильтонов цикл.
Теорема. Достаточное условие Гамильтоновости графа.
Если в связном графе с числом вершин 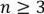 ,
,  , то граф Гамильтонов.
, то граф Гамильтонов.
Следствие.
Если в связном графе с числом вершин  степень любой вершины
степень любой вершины  , то граф гамильтонов.
, то граф гамильтонов.
Доказательство. Без доказательства.
40.Алгоритм построения минимального покрывающего дерева сети. Теорема о корректности алгоритма.
Сеть – связный граф  , с положительными весами на ребрах.
, с положительными весами на ребрах.
Покрывающее дерево -  , где
, где  .
.
Весом сети называется сумма весов всех ребер.
Минимальное покрывающее дерево сети – покрывающее дерево сети, имеющее наименьший вес среди всех покрывающих сетей.
Алгоритм построения минимального покрывающего дерева сети.
1)Отсортируем список всех ребер, в порядке возрастания весов. 2)1-ое ребро окрашивается, его вершины образуют компоненту. 3)Выбирается очередное ребро из списка:
а) Вершины, являющиеся концами ребра, принадлежат одной и той же компоненте, значит, ребро не окрашивается, состав компоненты не меняется.
б) Вершины принадлежат разным компонентам. Ребро окрашивается, компоненты сливаются.
в) Одна вершина принадлежит одной компоненте, вторая не принадлежит какой-либо компоненте. Ребро окрашивается, вершина добавляется к компоненте.
г) Вершины не принадлежат компонентам. Ребро окрашивается, вершины образуют новую компоненту.
4)Если все вершины в одной компоненте, алгоритм закончен, иначе – шаг 3.
Теорема о корректности алгоритма.
Пусть  ,
,  – минимальное покрывающее дерево.
– минимальное покрывающее дерево.
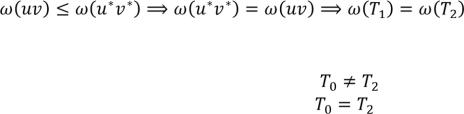
Доказательство.
Покажем, что это дерево.
 – произвольные вершины. Тогда, в сети
– произвольные вершины. Тогда, в сети  существует цепь, соединяющая
существует цепь, соединяющая 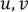 . Каждое ребро или окрашивается, или не окрашивается. Если окрашивается, то все вершины входят в одну компоненту, если не окрашивается, то
. Каждое ребро или окрашивается, или не окрашивается. Если окрашивается, то все вершины входят в одну компоненту, если не окрашивается, то  уже принадлежат компоненте, то есть существует путь, который связывает вершины
уже принадлежат компоненте, то есть существует путь, который связывает вершины  и. Тогда
и. Тогда  – связный граф, осталось доказать, что он без циклов.
– связный граф, осталось доказать, что он без циклов.
От противного: пусть в  есть цикл.
есть цикл.
Рассмотрим ребро  . Существует путь, который связывает
. Существует путь, который связывает  и
и  , но ребро
, но ребро  не должно окрашиваться.
не должно окрашиваться.
Цикла по неокрашенным ребрам быть не может, значит,  – это покрывающее дерево. Покажем, что
– это покрывающее дерево. Покажем, что  – минимальное покрывающее дерево.
– минимальное покрывающее дерево.
Возьмем произвольное покрывающее дерево сети  .
.  и
и  – разные деревья, то есть найдется ребро, которое есть в
– разные деревья, то есть найдется ребро, которое есть в  ,и нет в
,и нет в  . Пусть это ребро
. Пусть это ребро  .
.
 и
и  соединяются единственной цепью
соединяются единственной цепью  . Найдется ребро в цепи
. Найдется ребро в цепи  , которого нет в
, которого нет в  , пусть это
, пусть это  .
.
По дереву  построим дерево
построим дерево  .
.
Если вершины в  соединены цепью, то и вершины в
соединены цепью, то и вершины в  соединены цепью, то есть
соединены цепью, то есть
 – связный граф.
– связный граф.
Покажем, что  – покрывающее дерево. От противного: в
– покрывающее дерево. От противного: в  есть цикл
есть цикл  .
.
Тогда 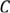 должен содержать ребро
должен содержать ребро  , то этот цикл будет в
, то этот цикл будет в 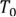 и ребро
и ребро  , иначе, этот цикл будет в
, иначе, этот цикл будет в 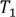 .
.  – связный граф без циклов.
– связный граф без циклов.  – покрывающее дерево.
– покрывающее дерево.
Покажем, что  – минимальное покрывающее дерево. Обозначим
– минимальное покрывающее дерево. Обозначим  – вес дерева.
– вес дерева.
 ,
,  – минимальное покрывающее дерево. Вес
– минимальное покрывающее дерево. Вес 
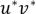 просматривается раньше, чем
просматривается раньше, чем  . Поскольку
. Поскольку 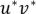 отсутствует в
отсутствует в  , то есть в
, то есть в  существует цепь. Это неверно,
существует цепь. Это неверно,  просматривается раньше
просматривается раньше  , тогда
, тогда
 – минимальное покрывающее дерево, значит,
– минимальное покрывающее дерево, значит,  – минимальное покрывающее дерево.
– минимальное покрывающее дерево.  имеет на одно ребро с
имеет на одно ребро с  больше, чем
больше, чем  . Если
. Если  , то теорема доказана.
, то теорема доказана.
41.Маршрут, путь, ориентированная цепь( бесконтурный путь), контур.
________________________________Орграфы_________________________________
Маршрут – последовательность смежных дуг. (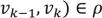 В маршруте дуги могут повторяться.
В маршруте дуги могут повторяться.

Циклический маршрут – маршрут, в котором начальная вершина совпадает с конечной.
Длина маршрута – количество дуг, входящих в состав маршрута.
Путь – маршрут, в котором каждая дуга встречается не более одного раза.
Простой путь – путь, в котором каждая вершина принадлежит не более чем 2 дугам. Контур – простой циклический путь.
Бесконтурный путь (ориентированная цепь) – простой нециклический путь.
42.Отношение достижимости, матрица достижимости, рекуррентная формула для построения матрицы достижимости; необходимое и достаточное условие, чтобы отношение достижимости являлось
порядком. Связный и сильно связный орграф.
Вершина  достижима из вершины
достижима из вершины  , если существует путь из
, если существует путь из  в
в  .
.
Если вершина  достижима из вершины
достижима из вершины 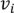 , то расстоянием от
, то расстоянием от  до
до  называется длина кратчайшего пути из
называется длина кратчайшего пути из  в
в  .
.
По определению считаем, что каждая вершина достижима сама из себя и удалена от себя на 0.
Связный орграф – орграф, симметризация которого является связной – убираем ориентацию и петли.
Сильно связный орграф – орграф с универсальным отношением взаимной достижимости.
Отношение достижимости есть отношение порядка на множестве вершин ографа т. и т. т., когда G – бесконтурный граф.
Рекуррентная формула нахождения матрицы достижимости.
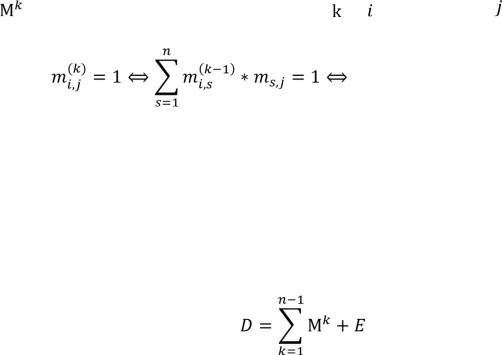
43.Матричное условие достижимости вершин. Следствие. Матричное условие взаимной достижимости двух вершин;
2 вершины взаимно достижимы, если они достижимы друг из друга. Отношение взаимной достижимости обладает свойствами: рефлексивность, симметричность.
Отношение эквивалентности.
То можно говорить о классах отношения эквивалентности.
Не одноэлементные сильные компоненты – 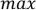 сильно связные подграфы.
сильно связные подграфы.
Теорема. Матричное условие существования маршрута длины k.
Пусть = ( , ) – орграф,  – матрица смежности. Справедлива теорема.
– матрица смежности. Справедлива теорема.
= 1 матрицы , когда существует маршрут длины из -ой вершины в -ую.
,
Доказательство.
, когда существует  , такое, что:
, такое, что:  . По индукции (для
. По индукции (для  верно).
верно).
Предположим, что это справедливо для всех  . Докажем для
. Докажем для  :
:
Если верно для  и будет существовать дуга, то верно для
и будет существовать дуга, то верно для  . (
. ( )
)
Следствие(исходное).
В n-вершинном орграфе 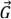 ,
, 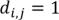 матрицы достижимости
матрицы достижимости
, когда вершина  достижима из вершины
достижима из вершины 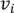 .
.
Теорема. Матричное условие взаимной достижимости.
Вершины  взаимно достижимы , когда соответствующие им строки в матрице достижимости равны.
взаимно достижимы , когда соответствующие им строки в матрице достижимости равны.
Доказательство.
Необходимость.
Пусть  взаимно достижимы.
взаимно достижимы.
Если вершина  достижима из
достижима из  и
и , то стоят единицы в строках, если нет – то не стоят. Значит, строки равны.
, то стоят единицы в строках, если нет – то не стоят. Значит, строки равны.
Достаточность.
Пусть строки  и
и равны (вершина достижима сама из себя). Тогда элемент
равны (вершина достижима сама из себя). Тогда элемент  , аналогично
, аналогично 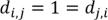 (вершины взаимно достижимы)
(вершины взаимно достижимы)
44.Отношение взаимной достижимости. Источники и стоки. База орграфа. Теорема о базе;
2 вершины взаимно достижимы, если они достижимы друг из друга. Отношение взаимной достижимости обладает свойствами: рефлексивность, симметричность.
Источник – вершина орграфа, недостижимая из любой другой вершины.
Сток – вершина орграфа, из которой недостижима любая другая вершина. Изолированная вершина является и источником, и стоком.
База орграфа – подмножество  ,такое, что любая вершина орграфа
,такое, что любая вершина орграфа  достижима из вершины базы, а любые 2 различные вершины базы не взаимно достижимы.
достижима из вершины базы, а любые 2 различные вершины базы не взаимно достижимы.
Фактор-граф – орграф 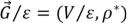 , где
, где  – отношение взаимной достижимости. Если
– отношение взаимной достижимости. Если  .
.
Теорема о базе. Подмножество 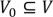 является базой орграфа , когда оно образовано вершинами, взятыми по одной из каждого источника фактор-графа.
является базой орграфа , когда оно образовано вершинами, взятыми по одной из каждого источника фактор-графа.
Доказательство.
Необходимость.
Пусть  – база орграфа.
– база орграфа.
Если  – источник фактор-графа, то он не достижим из любой другой вершины фактора графа (представитель этого слоя должен принадлежать базе).
– источник фактор-графа, то он не достижим из любой другой вершины фактора графа (представитель этого слоя должен принадлежать базе).
Достаточность.
Пусть  образовано вершинами, взятыми по одной из каждого источника факторграфа.
образовано вершинами, взятыми по одной из каждого источника факторграфа.
Возьмем произвольную  и рассмотрим слой
и рассмотрим слой 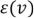 . Это вершина орграфа, если это не источник, то в нее входит какая-то дуга
. Это вершина орграфа, если это не источник, то в нее входит какая-то дуга 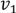 .
.
Поскольку фактор-граф – бесконтурный граф, то мы рано или поздно доберемся до источника (эта вершин достижима). Значит,  будет базой.
будет базой.
45.Необходимое и достаточное условие, для того, чтобы орграф был Эйлеровым. Необходимое и достаточное условие для существования
Эйлерова пути в орграфе.
Эйлеров путь – путь длины m (в данном случае, ребро – дуга в обе стороны) Эйлеров орграф – орграф, в котором есть циклический Эйлеров путь.
Связный орграф – орграф, симметризация которого является связной – убираем ориентацию и петли.
Теорема. Критерий эйлеровости орграфа.
Связный орграф Эйлеров , когда для любой вершины степень ее исхода равна степени захода. Без доказательства.
Теорема. Критерий существования Эйлерова пути в орграфе.
