Дискретка / diskretochka (1)
.pdf
Оглавление |
|
|
|
1.Комбинаторика, правило суммы и произведения. Размещения с повторениями и без |
|||
повторений. .............................................................................................................................. |
|
|
4 |
2.Перестановки с повторениями и без повторений. Сочетания с повторениями и без |
|||
повторений, свойства биномиальных коэффициентов. ...................................................... |
4 |
||
3.Сколькими способами можно разложить |
предметов одного сорта,…, |
|
|
предметов k-го сорта в 2 ящика? Следствия. ....................................................................... |
|
5 |
|
4.Даны n различных предметов и k ящиков. Надо положить в первый ящик |
|
||
предметов,…, в k-тый - |
, где |
. Сколькими способами можно |
|
сделать такое распределение, если не интересует порядок распределения предметов в |
|||
ящике?....................................................................................................................................... |
|
|
5 |
5.Даны n различных предметов и k одинаковых ящиков. Надо положить в каждый |
|||
ящик n=n/k предметов. Сколькими способами можно сделать такое распределение, |
|||
если не интересует порядок предметов в ящике? ................................................................ |
|
5 |
|
6.Сколькими способами можно распределить n одинаковых предметов в k ящиков?.... |
5 |
||
7.Сколько существует способов разложить n различных предметов в k ящиков, если |
|||
нет никаких ограничений? ..................................................................................................... |
|
|
6 |
8.Сколькими способами можно положить n различных предметов в k ящиков, если не |
|||
должно быть пустых ящиков?................................................................................................ |
|
6 |
|
9.Имеется предметов |
одного сорта,…, |
предметов s-ого сорта. Сколькими |
|
способами их можно разложить по k ящикам, если не должно быть пустых ящиков?... |
6 |
||
11.Сколько существует способов разложить n различных предметов в k различных |
|||
ящиков, с учетом расположения предметов в ящиках, если не все n предметов могут |
|||
быть использованы и некоторые ящики могут быть пустыми? Следствие. ..................... |
7 |
||
12.Формула включения-исключения..................................................................................... |
|
7 |
|
13.Полиномиальная формула. Свойства полиномиальных коэффициентов. ................... |
8 |
||
14.Реккурентное соотношение k-ого порядка, решение рекуррентного соотношения, |
|||
общее решение. Решение линейных рекуррентных соотношений с постоянными |
|||
коэффициентами k-ого порядка. ............................................................................................ |
|
9 |
|
15.Линейные рекуррентные соотношения, с постоянными коэффициентами второго |
|||
порядка. Свойства решений. ................................................................................................ |
|
10 |
|
16. Решение линейных рекуррентных соотношений с постоянными коэффициентами |
|||
второго порядка, в случае равных и различных корней характеристического |
|||
уравнения. .............................................................................................................................. |
|
|
10 |
17. Теорема об общем решении линейных рекуррентных соотношений с постоянными |
|
коэффициентами k- го порядка. Решение рекуррентных соотношений с постоянными |
|
коэффициентами k- го порядка с помощью характеристического уравнения. .............. |
11 |
18.Производящая функция. Сумма производящих функций, операция подстановки... |
12 |
19.Произведение и деление производящих функций. ....................................................... |
13 |
20. Теорема о разложении функции. ................................................................................... |
14 |
21.Теорема о производящей функции для последовательности, задаваемой линейным |
|
рекуррентным соотношением. Теорема о рациональной производящей функции. ...... |
15 |
22.Решение рекуррентных соотношений с помощью производящих функций. ............ |
16 |
23.Ориентированные и неориентированные графы. ......................................................... |
16 |
24.Полный граф, дополнение, объединение, соединение графов. ................................... |
17 |
25.Теорема о степенном множестве. ................................................................................... |
17 |
26.Теорема о соотношении суммы степеней вершин и числа ребер ............................... |
18 |
27.Алгоритм построения графа, по вектору степеней....................................................... |
18 |
28.Изоморфизм графов. Теорема об изоморфизме графов. .............................................. |
19 |
29.Проверка на изоморфизм 2-х графов по их матрицам смежности.............................. |
19 |
30.Часть графа, подграфы. Путь, цикл, цепь, длина пути и расстояние между |
|
вершинами. Достаточное условие связности нечетных вершин...................................... |
20 |
31.Достаточное условие связности графа. .......................................................................... |
20 |
32.Необходимое и достаточное условие неразделимости связного графа...................... |
21 |
33.Планарность. Дерево, плоское изображение дерева..................................................... |
21 |
34.Необходимое и достаточное условие для того, чтобы граф был деревом. ................ |
22 |
35.Формула Эйлера. Следствия из формулы Эйлера. ....................................................... |
23 |
36.Необходимое и достаточное условие планарности графа. .......................................... |
24 |
37.Эйлеров граф. Необходимое и достаточное условие для того, чтобы граф был |
|
Эйлеровым. ............................................................................................................................ |
25 |
38.Необходимое и достаточное условие существования Эйлерова пути........................ |
25 |
39.Гамильтонов граф. Достаточное условие гамильтоновости графа. ............................ |
26 |
40.Алгоритм построения минимального покрывающего дерева сети. Теорема о |
|
корректности алгоритма. ...................................................................................................... |
26 |
41.Маршрут, путь, ориентированная цепь( бесконтурный путь), контур....................... |
27 |
42.Отношение достижимости, матрица достижимости, рекуррентная формула для |
|
построения матрицы достижимости; необходимое и достаточное условие, чтобы |
|
отношение достижимости являлось порядком. Связный и сильно связный орграф. .... |
28 |
43.Матричное условие достижимости вершин. Следствие. Матричное условие |
|
взаимной достижимости двух вершин;............................................................................... |
29 |
44.Отношение взаимной достижимости. Источники и стоки. База орграфа. Теорема о |
|
базе;......................................................................................................................................... |
30 |
45.Необходимое и достаточное условие, для того, чтобы орграф был Эйлеровым. |
|
Необходимое и достаточное условие для существования Эйлерова пути в орграфе.... |
30 |
46.Обход орграфа. Необходимое и достаточное условие существования обхода. ........ |
31 |
47.Орсети, кратчайшие пути, алгоритм Дейкстры. ........................................................... |
31 |
1.Комбинаторика, правило суммы и произведения. Размещения с повторениями и без повторений.
Комбинаторика – раздел математики, посвященный решению задач выбора и расстановки элементов некоторого, обычно конечного множества, по определенным правилам. Каждое такое правило определяет способ построения некоторой конструкции из элементов исходного множества, называемой комбинаторной конфигурацией.
Правило суммы. Если выбор объекта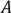 
можно осуществить n-способами, а выбор объекта 
m-способами, то выбор, либо 
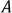, либо 
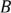можно осуществить n+m способами.
Правило произведения. Если выбор объекта |
можно осуществить n-способами, |
и |
после каждого такого способа, выбор объекта |
можно осуществить m-способами, |
то |
пару ( , ) можно осуществить n*m способами. |
|
|
Размещениями с повторениями из n-типов по k-элементам (k и n в любом соотношении) называются все k-элементные последовательности из n-типов,
отличающиеся порядком следования, или составом элементов.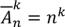 
Размещениями без повторений из n-типов по k-элементам (k<n) называются все последовательности k-различных элементов из n-типов, отличающиеся порядком
следования, или составом элементов.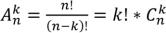 
.
2.Перестановки с повторениями и без повторений. Сочетания с повторениями и без повторений, свойства биномиальных
коэффициентов.
Перестановками без повторений из n-различных элементов, называются все возможные последовательности из этих n-элементов.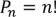 
Перестановками с повторениями из n-элементов k-типов называются все
возможные последовательности из n-элементов.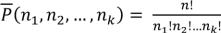
. Сочетаниями без повторений из n-типов по k-элементам (k≤n) называются все последовательности k-различных элементов из n-типов, отличающиеся составом
элементов.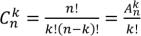 
.
3.Сколькими способами можно разложить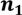 
предметов одного сорта,…, 
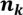предметов k-го сорта в 2 ящика? Следствия.
Так как в каждый ящик может попасть от 0 до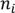 
предметов i-го сорта (во второй все оставшиеся), по правилу произведения получаем (
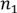+1)*(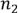
+1)*...*(
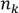+1) способов раскладки.
Следствие 1. Если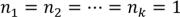 
, то их можно разложить 
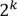способами. Следствие 2. Если в каждый ящик нужно положить не менее 
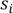предметов i-того сорта, то получаем: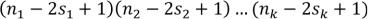
4.Даны n различных предметов и k ящиков. Надо положить в первый ящик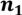 
предметов,…, в k-тый - 
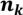, где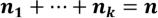 
. Сколькими
способами можно сделать такое распределение, если не интересует порядок распределения предметов в ящике?
Так как элементы 1-го типа можно переставлять 
способами,…, k-го типа nk! способами, то по правилу произведения элементы перестановки можно переставить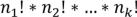 
способами так, что она останется неизменной. То же самое верно и для любого другого расположения элементов. Поэтому множество всех n! перестановок распадается на части, состоящие из 
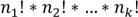одинаковых перестановок каждая. Поэтому число различных перестановок с повторениями,
равно: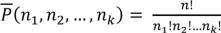
.
5.Даны n различных предметов и k одинаковых ящиков. Надо положить в каждый ящик n=n/k предметов. Сколькими способами
можно сделать такое распределение, если не интересует порядок предметов в ящике?
Так как ящики не пронумерованы, то их тоже нужно переставлять, число таких перестановок, равно k!. Поэтому, полученный в предыдущей задаче результат
необходимо разделить на k!. Получаем: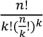
.
6.Сколькими способами можно распределить n одинаковых предметов в k ящиков?
Выложим все предметы в один ряд, добавим к ним k–1 одинаковых разделяющих предмета. Переставим всеми возможными способами n данных одинаковых предметов и k–1 разделяющих. Каждая такая перестановка определяет один из
способов распределения. А именно, предметы, расположенные до первого разделителя, положим в первый ящик, предметы, расположенные между первым и вторым разделителем – во второй ящик и так далее, предметы расположенный после k–1 разделителя, – в k ящик. По формуле перестановок с повторениями число таких
перестановок равно: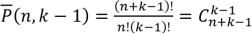 
.
7.Сколько существует способов разложить n различных предметов в k ящиков, если нет никаких ограничений?
Так как каждый предмет можно положить в любой из k ящиков, получаем: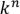
.
8.Сколькими способами можно положить n различных предметов в k ящиков, если не должно быть пустых ящиков?
Пусть r ящиков – пустые (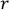 
=1,2,3,…,k-1). 
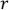пустых ящиков можно выбрать 
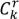способами, а в оставшихся 
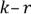ящиках предметы можно разложить 
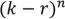способами. Тогда число распределений, при которых нет пустых ящиков, равно:
9.Имеется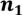 
предметов одного сорта,…, 
предметов s-ого сорта. Сколькими способами их можно разложить по k ящикам, если не
должно быть пустых ящиков?
10.Сколько существует способов разложить n различных предметов в k различных ящиков, с учетом расположения предметов в ящиках, если все предметы должны быть использованы? Следствие.
Выложим все предметы в один ряд, добавим к ним k–1 одинаковых разделяющих предмета. Переставим всеми возможными способами n данных различных предметов и k–1 разделяющих. Каждая такая перестановка определяет один из способов распределения. Представим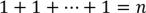 
, тогда всего таких перестановок:
.
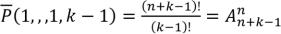Следствие: n! Cnk−−11 – нет пустых ящиков
11.Сколько существует способов разложить n различных предметов в k различных ящиков, с учетом расположения предметов в ящиках,
если не все n предметов могут быть использованы и некоторые ящики могут быть пустыми? Следствие.
Разобьем все возможные комбинации на классы. В s класс войдут комбинации, в которых использованы ровно s предметов. Из предыдущей задачи известно, что s
предметов можно разложить по k ящикам |
способами. s предметов из данных n |
|
можно выбрать способами. |
|
|
Всего в s класс войдут |
комбинаций. |
|
По правилу суммы получаем число способов разложить n различных предметов в k различных ящиков, с учетом расположения предметов в ящиках, если не все n
предметов |
могут |
быть использованы и |
|
некоторые ящики |
могут |
|||
быть пустыми: |
|
|
. |
|
|
|
||
|
|
|
|
|
=0 |
|
+−1 |
|
Следствие: |
n |
−1 |
! – нет пустых ящиков |
|
|
|
|
|
|
s=k |
|
−1 |
|
|
|
|
|
12.Формула включения-исключения.
Пусть А - конечное непустое множество.
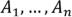– система подмножеств множества А. Тогда:
Доказательство.
Пример.
Пересечение будем учитывать дважды, 1 раз нужно отнять.
13.Полиномиальная формула. Свойства полиномиальных коэффициентов.
Формула бинома Ньютона.
Полиномом называется выражение: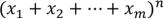 
(1).
Полиномиальной формулой называется формула для вычисления выражения типа (1), при любом m и n.
Теорема. Полиномиальная формула.
, где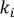 
– разбиение числа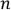 
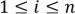
Доказательство.
(n раз) =
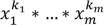, где 
. 
(
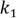штук),
,…,
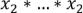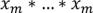
Свойства полиномиальных коэффициентов.
1)
2)
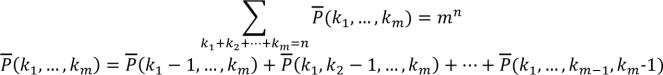
Доказательство.
Запишем полиномиальную формулу.
Умножаем обе части на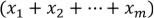 
.
…
14.Рекуррентное соотношение k-ого порядка, решение рекуррентного соотношения, общее решение. Решение линейных рекуррентных
соотношений с постоянными коэффициентами k-ого порядка.
Решением рекуррентного соотношения k-ого порядка называется числовая последовательность, обращающая данное рекуррентное соотношение в верное равенство, при подстановке в него общего члена последовательности.
Начальными условиями рекуррентного соотношения k-ого порядка называются первые k-членов последовательности, являющихся решением данного рекуррентного соотношения.
Общим решением рекуррентного соотношения k-ого порядка называется решение этого соотношения, которое зависит от k произвольных постоянных, путем подбора которых, можно получить любое решение данного рекуррентного соотношения k-ого порядка.
15.Линейные рекуррентные соотношения, с постоянными коэффициентами второго порядка. Свойства решений.
16. Решение линейных рекуррентных соотношений с постоянными коэффициентами второго порядка, в случае равных и различных
корней характеристического уравнения.
Решение линейного рекуррентного соотношение второго порядка в случае
различных корней: 1 |
≠ 2 – два корня характеристического уравнения. Тогда = |
||||
– решение. , – решение, , – решение, + - решение. |
|||||
1 |
2 |
1 |
2 |
1 |
2 |