Министерство образования и науки Российской Федерации

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИМЕНИ Н.Г. ЧЕРНЫШЕВСКОГО»

Практика по теории графов

ОТЧЕТ

студентки 3 курса 311 группы

направления 02.03.02 Фундаментальная информатика и информационные технологии

факультета компьютерных наук и информационных технологий

Филатовой Ольги Владимировны

Проверил

ассистент ____________ А. А. Казачкова

Саратов 2020

Оглавление

Базовый класс Граф 3

Ia - Вывести все изолированные вершины орграфа (степени 0). 5

Ia - Вывести те вершины орграфа, в которых есть петли. 5

Iб - Построить граф, являющийся симметрической разностью двух заданных. 6

II - Найти все вершины орграфа, из которых существует путь в данную. 7

II - Определить, от какой из вершин u₁ и u₂ путь до v короче (по числу рёбер). 8

III - Дан взвешенный неориентированный граф из N вершин и M ребер. Требуется найти в нем каркас минимального веса с помощью алгоритма Краскала 9

IV а (Дейкстра) - Вывести длины кратчайших путей для всех пар вершин. 11

IV b (Форд-Беллман) - Вывести все кратчайшие пути из вершины u. 13

IV с (Флойд) - Определить множество вершин орграфа, расстояние от которых до заданной вершины не более N. 14

V Нахождение максимального потока – алгоритм Диница 17

Базовый класс Граф

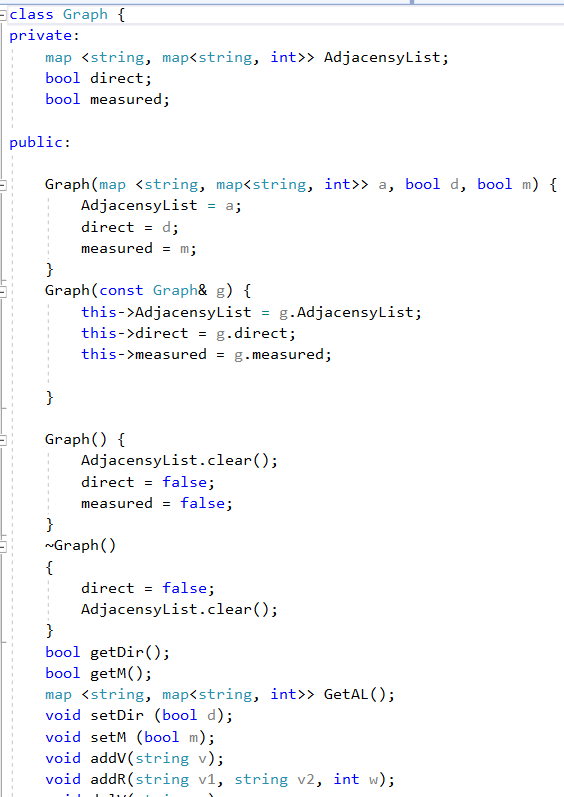
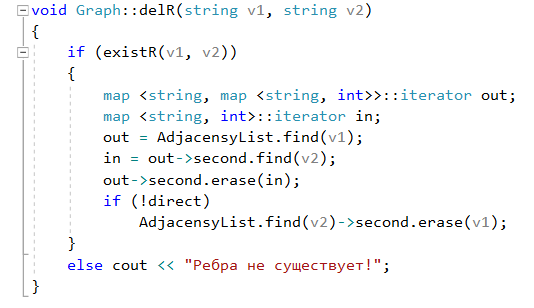
Ia - Вывести все изолированные вершины орграфа (степени 0).

Пытаемся найти смежные вершины. Если их нет – вершина изолирована.

Ia - Вывести те вершины орграфа, в которых есть петли.

Если среди смежных вершин текущей вершин находим ее же имя – петля есть

Iб - Построить граф, являющийся симметрической разностью двух заданных.

У двух графов множество вершин совпадает. В результирующий граф попадают те ребра, которые принадлежат множеству ребер либо первого графа, либо второго

II - Найти все вершины орграфа, из которых существует путь в данную.

Представлена нерекурсивная версия обхода в глубину. Вместе с обходом заполняется массив предков. С помощью него происходит восстановление пути. По заданию: если путь из вершины в данную существует – запомнить эту вершину.

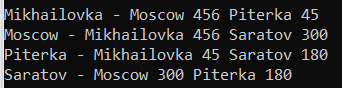
II - Определить, от какой из вершин u₁ и u₂ путь до v короче (по числу рёбер).

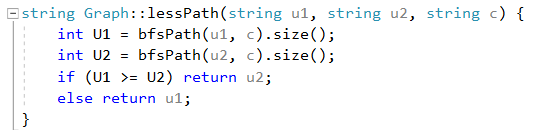
Представлена нерекурсивная версия обхода в ширину. Она отличается от предыдущего обхода тем, что здесь очередь, а не стек. Во время обходов заполняется массив предков, с помощью которого можно восстановить путь. Мы определяем, какой путь короче, сравнив длину двух векторов.

III - Дан взвешенный неориентированный граф из N вершин и M ребер. Требуется найти в нем каркас минимального веса с помощью алгоритма Краскала

Шаги для реализации алгоритма Краскала следующие:

1. Сортировать все ребра от малого веса до высокого.

2. Взять ребро с наименьшим весом и добавьте его в остовное дерево. Если добавление ребра создало цикл, то отклонить это ребро.

3. Продолжать добавлять ребра, пока всех вершины не будут достигнуты

4. Проверить, является ли остов деревом или же лесом (если кол-во ребер = кол-во вершин – 1, то это дерево)

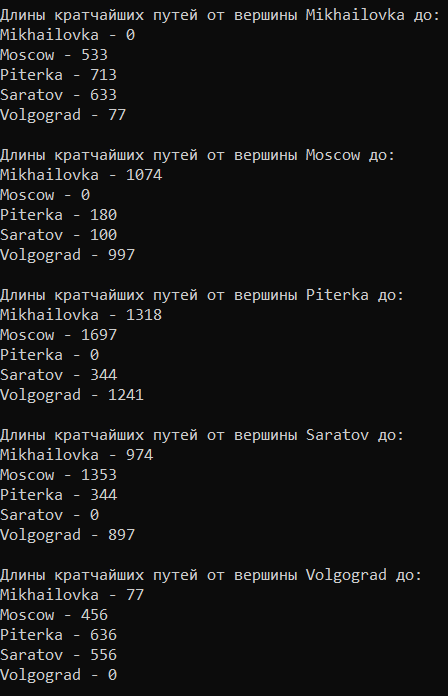
IV а (Дейкстра) - Вывести длины кратчайших путей для всех пар вершин.

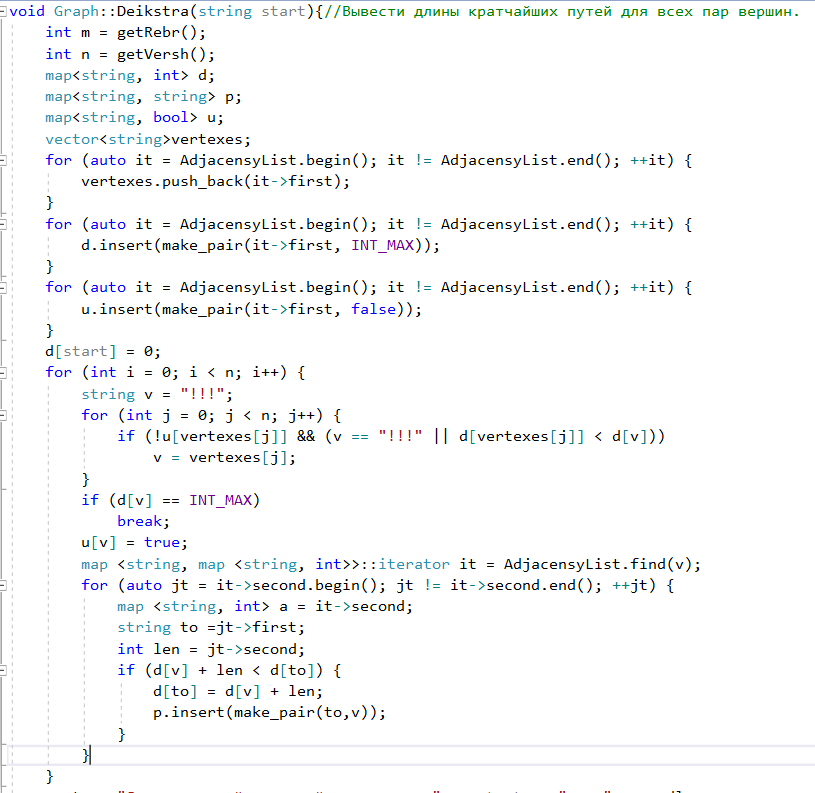
Алгоритм Дейкстры представляет собой   итераций, на каждой из которых выбирается непомеченная вершина с наименьшей величиной  , эта вершина помечается, и затем просматриваются все рёбра, исходящие из данной вершины, и вдоль каждого ребра делается попытка улучшить значение   на другом конце ребра.

IV b (Форд-Беллман) - Вывести все кратчайшие пути из вершины u.

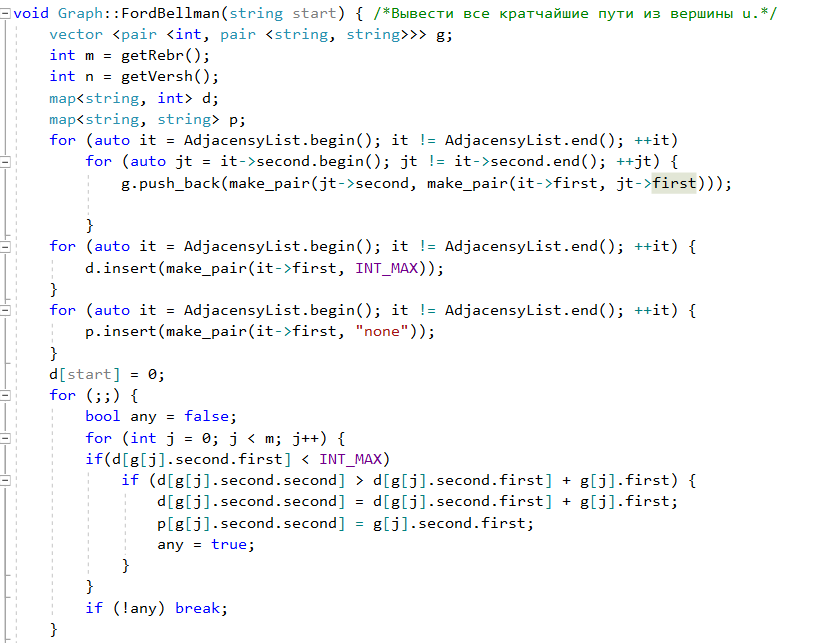
Сам алгоритм Форда-Беллмана представляет из себя несколько фаз. На каждой фазе просматриваются все рёбра графа, и алгоритм пытается произвести релаксацию вдоль каждого ребра   стоимости  . Релаксация вдоль ребра — это попытка улучшить значение   значением  . Фактически это значит, что мы пытаемся улучшить ответ для вершины  , пользуясь ребром   и текущим ответом для вершины  .

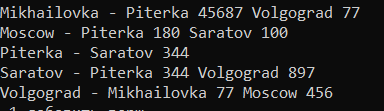
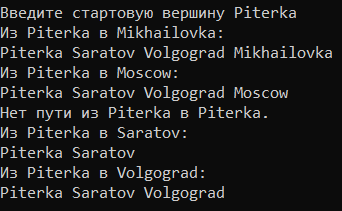
IV с (Флойд) - Определить множество вершин орграфа, расстояние от которых до заданной вершины не более N.

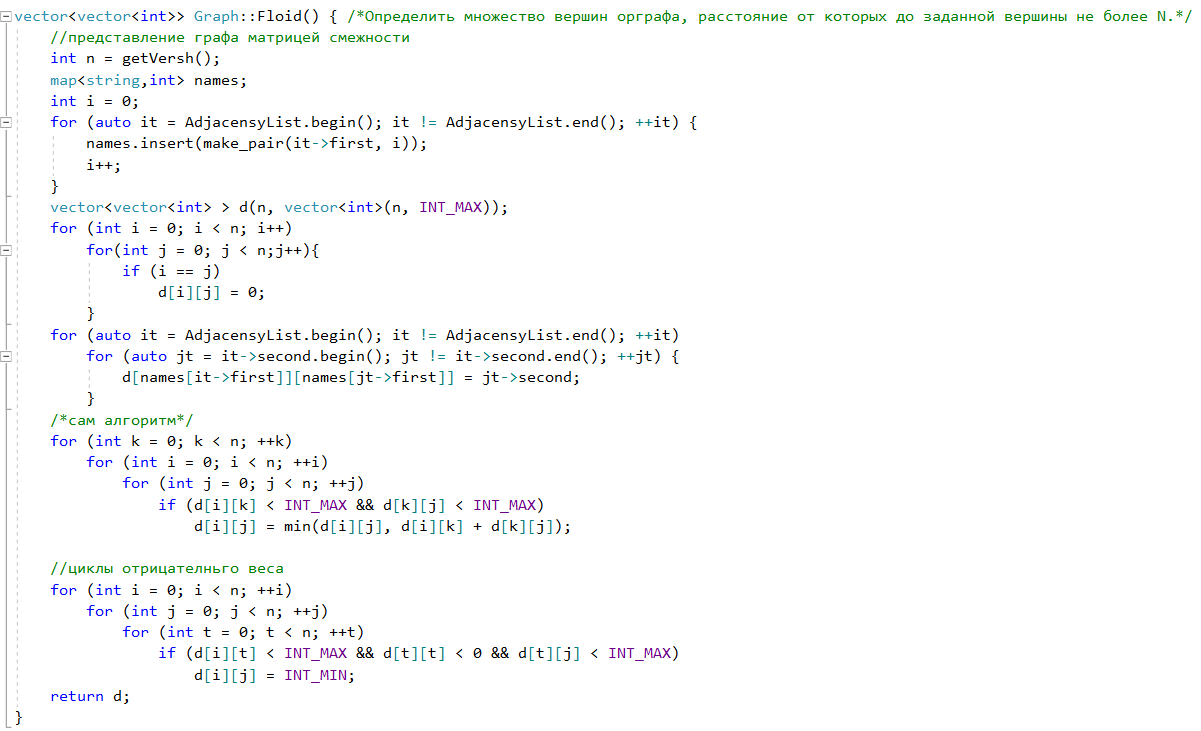
На вход программе подаётся граф, заданный в виде матрицы смежности — двумерного массива   размера  , в котором каждый элемент задаёт длину ребра между соответствующими вершинами. Требуется, чтобы выполнялось   для любых  .

Предполагается, что если между двумя какими-то вершинами нет ребра, то в матрице смежности было записано какое-то большое число (достаточно большое, чтобы оно было больше длины любого пути в этом графе); тогда это ребро всегда будет невыгодно брать, и алгоритм сработает правильно. Если в графе существуют отрицательные циклы, можно сделать, например, следующий критерий "не существования пути". Итак, пусть на данном графе отработал обычный алгоритм Флойда. Тогда между вершинами   и   не существует кратчайшего пути тогда и только тогда, когда найдётся такая вершина  , достижимая из   и из которой достижима  , для которой выполняется  .

Кроме того, при использовании алгоритма Флойда для графов с отрицательными циклами следует помнить, что возникающие в процессе работы расстояния могут сильно уходить в минус, экспоненциально с каждой фазой. Поэтому следует принять меры против целочисленного переполнения, ограничив все расстояния снизу какой-нибудь величиной (например,  ).

Случай отрицательных циклов

V Нахождение максимального потока – алгоритм Диница

Искать   пути по одному, пока такие пути находятся. Путь можно найти за   обходом в глубину, однако удалять в процессе обхода в глубину из графа все "лишние" рёбра, т.е. рёбра, вдоль которых не получится дойти до стока.

Это очень легко реализовать: достаточно удалять ребро после того, как мы просмотрели его в обходе в глубину (кроме того случая, когда мы прошли вдоль ребра и нашли путь до стока). С точки зрения реализации, надо просто поддерживать в списке смежности каждой вершины указатель на первое неудалённое ребро, и увеличивать этот указать в цикле внутри обхода в глубину.

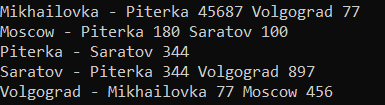
Граф предварительно должен быть представлен в виде матрицы, также необходимо задать сток и исток.

Обратные ребра:

Иногда обратные ребра выгодны, для того чтоб идти по более выгодному пути.

Если бы первый dfs нашёл путь 7 8 9 10 (блокирующий, который далеко не всегда совпадает с максимальным), второй dfs без обратных рёбер не смог бы найти путь 7 11 12 9 8 13 14 10. Ответ для задачи: 40