
матанал / matan_kollok_3_sem
.docx1. Гладкая поверхность. Ориентация поверхности. Площадь поверхности.
Поверхность называют гладкой, если она удовлетворяет трем условиям:
1) Множество D является замкнутым ограниченным элементарным мн-вом, граница γ которого представляет собой простой кусочный гладкий контур, а отображение, задаваемое рав-вами: x=x(u,v), y=y(u,v), z=z(u,v), (u, v) ∈ D ⊂ R2 взаимно однозначно на мн-ве внутренних точек D.
2) Функции x=x(u,v), y=y(u,v), z=z(u,v) и их частные производные первого порядка непрерывны на мн-ве D вплоть до контура γ.
3) Хотя бы один из якобианов отличен от нуля D(x,y)/D(u,v), D(y,z)/D(u,v), D(z,x)/D(u,v) при любых значениях х и у.
Выделение одной из сторон поверхности Ф с помощью параметризации называется ориентацией поверхности Ф.
Предел σ(T) при стремлении диаметра разбиения к нулю (h → 0) называют площадью поверхности Ф и обозначают через S, где σ(T) – сумма всех разбиений фигуры Ф на параллелограммы.
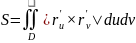 .
.
2. Поверхностный интеграл первого рода и теорема о его существовании.
Пусть
существует предел I
интегральной суммы
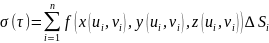 (где
(где
 )
при стремлении диаметра разбиения
измеримых по Жордану мн-в к нулю (
)
при стремлении диаметра разбиения
измеримых по Жордану мн-в к нулю (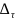 →
0), тогда I
называют поверхностным
интегралом первого рода
от функции f
по поверхности Ф.
→
0), тогда I
называют поверхностным
интегралом первого рода
от функции f
по поверхности Ф.
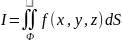 .
.
Т.
о существовании поверхностного интеграла
первого рода.
Пусть Ф – гладкий контур,
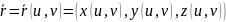 - его параметрическое представление.
Тогда поверхностный интеграл существует
и может быть вычислен по формуле:
- его параметрическое представление.
Тогда поверхностный интеграл существует
и может быть вычислен по формуле:
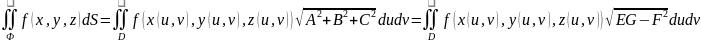 .
.
Док-во.
Обозначим
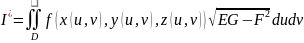 .
Тогда
.
Тогда
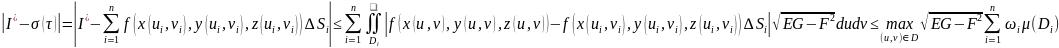 ,
где
,
где
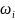 – колебание функции f
на мн-ве
– колебание функции f
на мн-ве
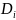 .
Последнее выражение стремится к нулю
при
→
0 в силу непрерывности функций f
и
.
Последнее выражение стремится к нулю
при
→
0 в силу непрерывности функций f
и
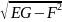 на замкнутом мн-ве D.
Таким образом, предел интегральной
суммы
на замкнутом мн-ве D.
Таким образом, предел интегральной
суммы
 равен
равен
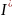 при
→
0.
при
→
0.
3. Поверхностный интеграл первого рода и его св-ва.
Пусть
Ф – гладкая поверхность с параметрическим
представлением
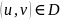 и на поверхности Ф заданы функции
P(x,y,z),
Q(x,y,z),
R(x,y,z).
Определим поверхностные
интегралы второго рода:
и на поверхности Ф заданы функции
P(x,y,z),
Q(x,y,z),
R(x,y,z).
Определим поверхностные
интегралы второго рода:
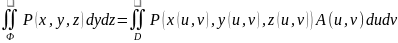
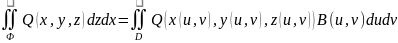
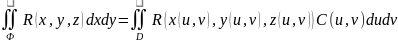
(можно записать в виде подынтегральной суммы).
Св-ва:
1) При смене ориентации поверхности интеграл меняет знак.
2) Интеграл обладает св-вом линейности (можно вытащить сумму Σ за знак интеграла).
3)
Если поверхность Ф разбита на конечное
число частей Фк
1<=k<=n,
не имеющих общих внутренних точек, то
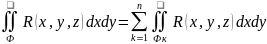 .
.
4)
Интеграл
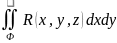 по цилиндрической поверхности Ф с
образующей, параллельной оси Oz,
равен нулю.
по цилиндрической поверхности Ф с
образующей, параллельной оси Oz,
равен нулю.
4. Формула Стокса.
Пусть в некоторой области G, полностью содержащей поверхность Ф, заданы непрерывно дифференцируемые функции P,Q,R. Тогда имеет место ф-ла Стокса:
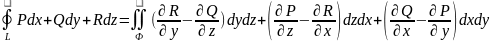
Док-во.
Док-м
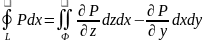 .
.
Преобразуем левую часть. Пусть контур L* задан параметрически u = u(t), v = v(t), t ∈ T = [t1, t2]. Тогда ур-ия, задающие контур L: x = x(u(t),v(t)), y = y(u(t),v(t)), z = z(u(t) v(t)), t ∈ T.
По
ф-лам для вычисления интеграла второго
рода:
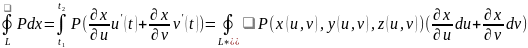 .
.
Для
правой части применим ф-лу Грина:
 .
.
Аналогично для Q и R. Суммируя полученные рав-ва, получим ф-лу Стокса.
5. Формула Остроградского-Гаусса.
Пусть
V
– простая замкнутая область, граница
Ф которой положительно ориентирована.
Если функции P(x,y,z),
Q(x,y,z), R(x,y,z) непрерывно дифференцируемы
в области G,
содержащей Ф, то верна ф-ла
Остроградского-Гаусса:
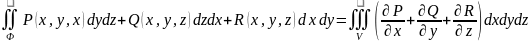 .
.
Док-во.
Док-м одно из трех равенств:
 .
Док-м для замкнутой правильной области
V
по направлению оси Оz.
По правилу вычисления тройного интеграла:
.
Док-м для замкнутой правильной области
V
по направлению оси Оz.
По правилу вычисления тройного интеграла:
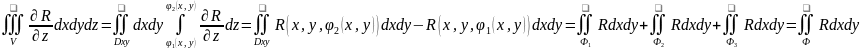 .
.
Простую
область V
разобьем на m
частичных областей Vk,
k = 1,…,m,
правильных в направлении оси
Оz,
ограниченных кусочно гладкими
поверхностями Фk.
Тогда
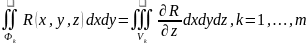 .
Просуммировав, получим:
.
Просуммировав, получим:
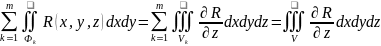 .
Для P,Q
аналогично.
.
Для P,Q
аналогично.
6. Тригонометрическая система, ортогональность тригонометрической системы и свойства интеграла от периодической функции.
Система функций ½,cos x, sin x, cos 2x,sin 2x,…,cos nx, sin nx, … называется тригонометрической системой.
Две
функции f
и g,
интегрируемые на [a,b],
называют взаимно ортогональными, если
 .
.
Т.
об ортогональности тригонометрической
системы.
Любые две функции тригонометрической
с-мы взаимно ортогональны на
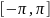 .
.
Док-во. При k<>n:
1)
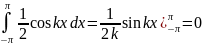 .
.
2)
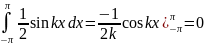 .
.
3)
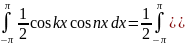 (аналогично для sin(kx)*sin(nx)
и sin(kx)*cos(nx)).
(аналогично для sin(kx)*sin(nx)
и sin(kx)*cos(nx)).
Т.
св-во интеграла от периодической ф-ции.
Пусть функция
 .
Тогда при любом
.
Тогда при любом
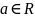
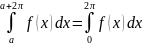 .
.
Док-во.
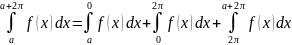 .
.
Сделаем
замену x=t+2π
в третьем слагаемом:
 .
Складывая, получим ф-лу из определения
теоремы.
.
Складывая, получим ф-лу из определения
теоремы.
7. Тригонометрический ряд. Коэффициенты Фурье и ряд Фурье. Ядро Дирихле.
Функциональный
ряд
 называется тригонометрическим
рядом, где
a0,a1,b1,…,an,bn,…
- вещественные числа – его коэффициенты.
называется тригонометрическим
рядом, где
a0,a1,b1,…,an,bn,…
- вещественные числа – его коэффициенты.
Пусть функции f определена и интегрируема на [-π, π]. Тогда числа a0,a1,b1,…,an,bn, вычисленные по ф-лам:
 наз. коэфф.
Фурье, а ряд
с этими коэфф. наз. рядом
Фурье функции
f.
наз. коэфф.
Фурье, а ряд
с этими коэфф. наз. рядом
Фурье функции
f.
Функцию
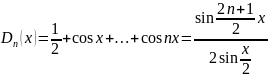 назыв. ядром
Дирихле.
назыв. ядром
Дирихле.
8. Представление частичной суммы ряда Фурье интегралом Дирихле.
Т.Дирихле.
Пусть ф-ция
.
Тогда частная сумма ряда Фурье ф-ции f
может быть представлена в виде:
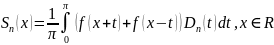 ,
где
.
,
где
.
Док-во.
Пусть ф-ция
.
Рассм. частную сумму ее ряда Фурье в
фиксированной точке х:
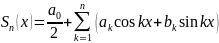 .
.
Подставим
вместо коэф. выражения и получим:
 .
.
Сделаем
замену t=x+u:
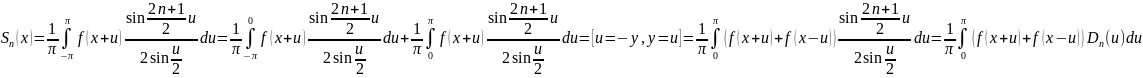 .
.
9.
Т. Римана-Лебега.
Пусть функция f
интегрируема на отрезке [a,b].
Тогда
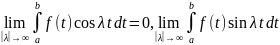 .
.
10. Принцип локализации Римана.
Т.
принцип
локализации Римана.
Пусть функция
.
Тогда при любом a∈(0,
π) частная
сумма ряда Фурье функции f
может быть представлена в виде:
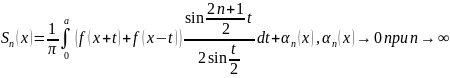 .
.
Док-во.
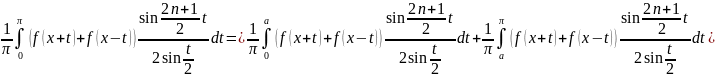 .
.
Обозначим
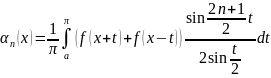 .
.
На
отрезке [a,
π] функция
 непрерывна и справедлива оценка
непрерывна и справедлива оценка
 .
Поэтому функция
.
Поэтому функция
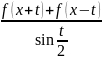 интегрируема на отрезке [a,
π]. Тогда
по т. Римана-Лебега
интегрируема на отрезке [a,
π]. Тогда
по т. Римана-Лебега
 .
.
11. Признак Дини поточечной сходимости рядов Фурье и три следствия.
Т.
Признак Дини
поточечной сходимости рядов Фурье.
Пусть функция
.
Если при некотором фиксированном х
сходится интеграл
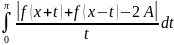 ,
где А – некоторое число, то в этой точке
х ряд Фурье функции f
сходится и имеет своим пределом числа
А.
,
где А – некоторое число, то в этой точке
х ряд Фурье функции f
сходится и имеет своим пределом числа
А.
Док-во.
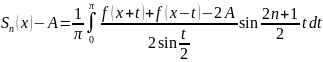 .
Если сходится
,
то сходится
.
Если сходится
,
то сходится
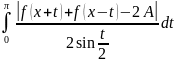 ,
т.к.
,
т.к.
 при
при
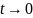 .
Тогда согласно обобщению т.Римана-Лебега:
.
Тогда согласно обобщению т.Римана-Лебега:
 ,
т.е.
,
т.е.
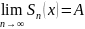 .
.
Следствия:
1)
Пусть функция
и дифференцируема в точке х. Тогда
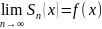 .
.
2)
Пусть функция
и существуют левосторонняя
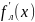 и правосторонняя
и правосторонняя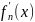 производные. Тогда
.
производные. Тогда
.
3)
Пусть функция
и существуют конечные пределы:
 .
Тогда
.
Тогда
 .
.
12. Некоторые особенности рядов Фурье: ряды Фурье четных и нечетных функций, разложение в ряд Фурье на промежутке [0,π], разложение в ряд Фурье на промежутке [-l,l].
Ой фу лень писат надеюсь этого вопроса не будет ыыыы если что в методичке стр 31-33
13. Средние Фейера и их представление интегралом Фейера.
Пусть
функция
,
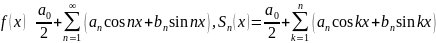 .
Средними
Фейера
называют
.
Средними
Фейера
называют
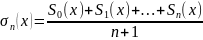 .
.
Т.
Пусть функция
.
Тогда верно представление
интеграла Фейера
 наз.
ядром Фейера.
наз.
ядром Фейера.
Док-во.
Докажем только ядро Фейера, т.к. в силу
этой верности, т.Дирихле и определения
средних Фейера теорема будет верна.
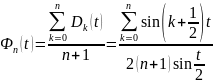 .
.
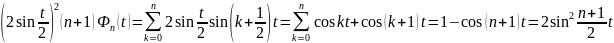 .
.
14.
Теорема
о суммируемости ряда Фурье методом
средних арифметических в точках разрыва.
Пусть функция
И в точке х сущ. предел
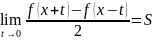 .
Тогда в точке х
.
Тогда в точке х
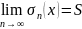 .
.
Док-во.
Пусть е > 0. Тогда
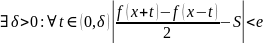 .
.
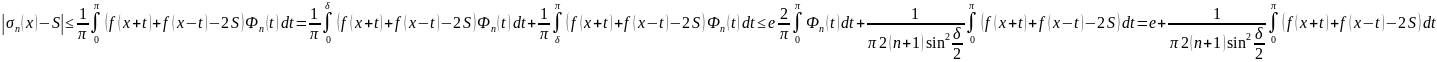 .
.
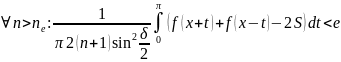 .
Тогда
.
Тогда
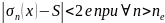 .
.
