моделирование / Моделирование5

МИНОБРНАУКИ РОССИИ

Федеральное государственное бюджетное образовательное учреждение высшего образования

«САРАТОВСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИМЕНИ Н. Г. ЧЕРНЫШЕВСКОГО»

ОТЧЁТ ПО ЗАДАНИЮ №5

Студентка 4 курса 411 группы

Направления 02.03.02—Фундаментальная информатика и информационные технологии

Факультета КНиИТ

Филатова Ольга Владимировна

Проверил

ассистент И.А.Люкшин

Саратов2022

СОДЕРЖАНИЕ

1. Задание 3

2. Код программы и результаты выполнения 4

Задание

Задача 19. Система состоит из двух новых элементов. В начальный момент времени начинают работать оба элемента. Длительность безотказной работы каждого из элементов есть нормально распределенная случайная величина с параметрами u и q . После отказа одного из элементов, длительность работы оставшегося элемента есть нормально распределенная случайная величина с параметрами u/ 10 и q/ 10 . После отказа второго элемента система перестает работать. Построить модель возникновения отказов в указанной системе. Провести 1000 испытаний с моделью и оценить математическое ожидание и среднее квадратическое отклонение длительности безотказной работы системы.

Код программы и результаты выполнения

Программа написана на высокоуровневом интерпретируемом языке Octave.

С помощью формулы нахождения нормального распределения 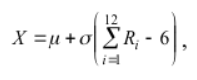находим время безотказной работы обоих элементов. Так как после отказа одного из них, система не прерывает работу, выбираем наименьшее из полученных значений и аналогично высчитываем время безотказной работы системы с одним работающим элементом. Сумма наименьшего и нового значения есть общая сумма работы системы. Значения мат. 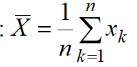ожидания и среднеквадратического отклонения находим по формулам и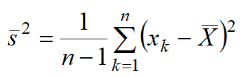

Код программы:

u = input("Введите первый параметр распределения:");

q = input("Введите второй параметр распределения:");

N=5;

SM = 0;

K = [];

for i = 1 : N

sum1 = 0.0;

for j = 1 : 12

sum1 += rand;

endfor

time1 = u + q * (sum1 - 6);

sum2 = 0.0;

for j = 1 : 12

sum2 += rand;

endfor

time2 = u + q * (sum2 - 6);

M = min([time1,time2]);

sum3=0.0;

for j=1 :12

sum3+=rand;

endfor

time3=u/10 + q/10 * (sum2 - 6);

time=M+time3;

SM += time;

K = [K,time];

disp(["Длительность безотказной работы: ", num2str(time)]);

endfor

KV = 0;

for i = 1 : N

KV += (K(i) - SM*(1/N))^2;

endfor

disp(["Математическое ожидание:",num2str(SM*(1/N))]);

disp(["Среднее квадратичное:",num2str(KV * (1/(N-1)))]);

Скриншоты результатов выполнения программы: