МОии / ПЗ 4 Обн. груб. погр

Практическое задание № 4

Сабитов И.А. ПБ-713

Порядок выполнения работы.

1. Импортировали данные в программу обработки Excel.

2. Построить график значений измерений.

Рис. 1. График значений измерений в Excel.

3. Упорядочить результаты измерений по возрастанию.

4. Определили измерения, значения которых, возможно, являются промахом. Для этого взяли из отсортированного массива 4 значения xmin и 4 значения xmax.

хmin	xmax
93,07	103,24
93,4	103,29
100,08	108,25
100,09	108,91

Таблица 1. Значения, которые могут являться промахом.

5. По всем измерениям рассчитали оценку

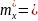101,4396

6. Рассчитали оценку дисперсии 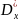и статистическое среднее квадратическое отклонение

=3,209596

=1,791534

7. Рассчитали υ.

Vmin	Vmax
4,671749	1,004949
4,48755	1,032858
0,758903	3,801434
0,753321	4,169833

Таблица 2. Расчет распределения нормализации величин.

8. Для доверительной вероятности α=0,95 и числа измерений n=100 из таблицы 1.1 в методических указаниях для выполнения ПЗ-3 взяли значение д=3,12.

9. На основании сравнения значений и д приняли решение. Результаты расчета записали в таблицу 3.

№	Проверяемое значение		д	Решение
1	93,07	4,671749	3,12	0
2	93,4	4,48755	3,12	0
3	100,08	0,758903	3,12	1
4	100,09	0,753321	3,12	1
5	103,24	1,004949	3,12	1
6	103,29	1,032858	3,12	1
7	108,25	3,801434	3,12	0
8	108,91	4,169833	3,12	0

Таблица 3. Результаты расчета и принятия решения.

0 – неверное значение; 1 – верное.

10. Убрали из исходной выборки найденные грубые ошибки и заново рассчитали .

101,4618

11. Аналогично делаем для MatLab.

Код программы:

fileID = fopen('r1.txt');

A = fscanf(fileID, '%f');

fclose(fileID);

B = sort(A);

n = 100;

mx=mean(B);

dx=cov(B);

Sigma=sqrt(dx);

v1=abs(B(1)-mx)/Sigma;

v2=abs(B(2)-mx)/Sigma;

v3=abs(B(3)-mx)/Sigma;

v4=abs(B(4)-mx)/Sigma;

v5=abs(B(97)-mx)/Sigma;

v6=abs(B(98)-mx)/Sigma;

v7=abs(B(99)-mx)/Sigma;

v8=abs(B(100)-mx)/Sigma;

plot(A, '.');

grid on;

C = B(3:98);

mx1=mean(C);

mx = 101.4396

dx =3.2096

Sigma = 1.7915

mx1 = 101.4618

Рис. 2. График значений измерений в MatLab.

Вывод:

В работе делали статистическую проверку гипотезы средствами Microsoft Excel и Matlab. Расчитав 8 значений распределения нормализованных величин мы сравнили их с допускаемым значением критерия (таблица 3) и приняли решение, что первые и последние два значения исходных данных следует отбросить как не согласующиеся с возможными значениями, которые может принимать в наблюдениях случайная величина. Сравнивая варианты обработки данных в этих программах можно сказать, что результаты расчетов совпали, но удобнее работать в Excel.