2.3.2 Магнитная проницаемость

Величины μ₀, μ и χ нелинейно зависят от Н и в соответствии с изложенным в п. 2.3.1 будут разными для разных видов кривых намагничивания. В дальнейшем нам достаточно использовать основную кривую намагничивания. Проницаемость, соответствующую этой кривой, называют нормальной (в дальнейшем слово «нормальная» опускается). В некоторой точке А (рис. 2.10, а)

μ = В_А/H_А = tgα.

а)

О

б)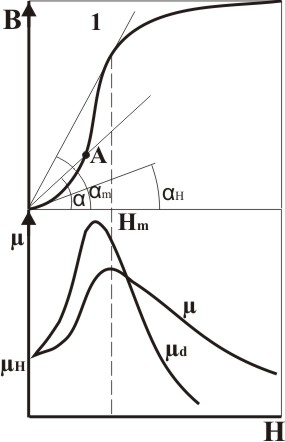

тношение В/Н можно рассматривать и как тангенс угла наклона к оси абсцисс прямой, проходящей через начало координат и точку с координатами (В_А, H_А). Так как тангенс – функция возрастающая, то большему углу соответствует большее отношение В/Н. Угол наклона – максимальный, если рассматриваемая прямая является касательной к кривой намагничивания (см. рис. 2.10).

Различают начальную μ_н = lim(В/H) = tgα_н и максимальную μ_max = tgα_m проницаемость. Часто используют понятие дифференциальной магнитной проницаемости:

μ_d = lim(ΔВ/ΔH) = dВ/dH.

Г

Рис. 2.10 Определение μ, μ_d

и их зависимости от Н:

1 – начальная кривая намагничивания; H_m – напряженность магнитного поля, соответствующая максимальному значению относительной магнитной

проницаемости

рафик зависимости В(Н) качественно отличается от графика J(Н) (рис. 2.11). Магнитная индукция внешнего поля (μ₀Н) линейно зависит от напряженности магнитного поля (кривая 1). Магнитная индукция элементарных токов (μ₀J) увеличивается до значения B_s, соответствующего насыщению при напряженности H_s. При дальнейшем увеличении Н она не изменяется (кривая 2). Кривая 3 индукции тела (В = μ₀H + μ₀J) получается сложением ординат кривых 1 и 2.

Рис. 2.11 Зависимость магнитной индукции В

и её составляющих от напряженности поля

2.3.3 Магнитный гистерезис

Характерной особенностью ферромагнетиков является то, что при уменьшении поля после намагничивания до некоторой величины В функция В(Н) будет иметь другой вид, чем при увеличении, и при Н = 0 окажется, что магнитная индукция В ≠ 0. Если построить график В = f(Н), уменьшая поле от некоторого значения +Н до –Н, а затем увеличивая от –Н до +Н, то получится кривая, напоминающая петлю, которая называется петлёй магнитного гистерезиса. Начиная измерения с различных Н, можно получить семейство петель гистерезиса (при этом их вершины лежат на основной кривой намагничивания). Однако существует поле Н_s, когда измерения со значением Н ≥ Н_s уже не дают новых петель, совпадая между собой. Петля гистерезиса, построенная при циклическом перемагничивании от +Н_s до –Н_s, называется предельной. Она является важнейшей характеристикой данного ферромагнетика.

Магнитной индукцией насыщения В_s (рис. 2.12) называют индукцию, соответствующую намагниченности насыщения J_s, когда с увеличением Н намагниченность не возрастает, а В увеличивается только за счет Н.

Остаточной магнитной индукцией В_r (см. рис. 2.12) называют индукцию, которая остается в предварительно намагниченном до насыщения ферромагнетике после снятия намагничивающего поля Н.

Коэрцитивной силой Н_с (см. рис. 2.12) называют величину размагничивающего поля, которое должно быть приложено, чтобы установить значение В = 0.

Можно говорить о В_r и Н_с для любых петель гистерезиса, однако обычно под остаточной индукцией и коэрцитивной силой и понимают (если это не оговаривается особо) их значения по предельной петле.

Рис. 2.12 Симметричная петля гистерезиса

Площадь петли гистерезиса равна работе Р, затраченной на перемагничивание единицы объема ферромагнетика, Дж/м³:

Р = ∫НdВ.

Часто используется понятие удельных потерь – затрат энергии на перемагничивание единицы массы ферромагнетика в единицу времени:

p_r = Sf/γ,

где S – площадь петли гистерезиса, измеренная в квазистатическом режиме, Тл А/м;

f – частота перемагничивания, Гц;

γ – удельная плотность материала, кг/м³.