
2 семестр лабы Шейнман БТС / ЛР 8 / 0501 Конунников ЛР8-1
.docxФедеральное государственное автономное образовательное учреждение высшего образования «Санкт–Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина)»
кафедра физики
ОТЧЕТ
по лабораторной работе № 8
«ИЗМЕРЕНИЕ СОПРОТИВЛЕНИЙ ТОКОПРОВОДЯЩИХ МОДЕЛЕЙ ПРИ ПОМОЩИ МОСТА УИТСТОНАЯ»
Выполнил: Конунников Г. А.
Группа № 0501
Преподаватель: Шейнман И. Л.
Вопросы |
|
Задачи ИДЗ |
Даты |
Итог |
|
||||
|
|
|
|
|
|
|
коллоквиума |
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Санкт–Петербург, 2021
ЛАБОРАТОРНАЯ РАБОТА № 8
ИЗМЕРЕНИЕ СОПРОТИВЛЕНИЙ ТОКОПРОВОДЯЩИХ МОДЕЛЕЙ ПРИ ПОМОЩИ МОСТА УИТСТОНАЯ
ЦЕЛЬ РАБОТЫ: ознакомление с методом измерения сопротивлений при помощи моста постоянного тока; приобретение навыков расчета сопротивления проводников переменного сечения; определение удельных сопротивлений материалов токопроводящих моделей.
ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ: стенд для сборки измерительной цепи; токопроводящие модели; магазины образцовых сопротивлений; нульиндикатор (гальванометр); источник тока.
ИСЛЕДУЕМЫЕ ЗАКОНОМЕРНОСТИ
Сопротивление проводников зависит от их формы и размеров, от рода вещества и его состояния:
|
(1) |
где l – длина проводника; S – площадь его поперечного сечения; – удельное сопротивление материала проводника.
Закон Ома в дифференциальной форме определяется по формуле (2):
|
(2) |
Закон Джоуля–Ленца в дифференциальной форме определяется по формуле (3):
|
(3) |
Сопротивление каждого отдельного проводника форме определяется по формуле (4):
|
(4) |
где S – площади поперечного сечения проводника, а сопротивление проводника на участке от точки 1 до точки 2 равно
|
(5) |
При этом выполняется соотношение (6):
|
(6) |
где R – сопротивление утечки между двумя электродами в проводящей среде с удельным сопротивлением ; C – взаимная электроемкость электродов в среде с относительной диэлектрической проницаемостью .
Взаимная электроемкость электродов рассчитывается по формуле (7):
|
(7) |
где Q – заряд на одном из электродов (на другом электроде имеется равный по модулю и противоположный по знаку заряд –Q); – разность потенциалов между электродами.
Разность потенциалов находится криволинейным интегрированием электрического поля:
|
(8) |
где El – касательная к пути интегрирования компонента вектора E.
Методика измерений
Измерительный
мост оборудован четырьмя резисторами
R1,
R2,
R3
–
известны, Rx
– требуется
определить. G1
– источник, P1
– гальванометр. Если UAC
делится между R1
и Rx
в соотношении R2
к R3
разность потенциалов, между B
и D
равна нулю тока через гальванометр нет
и Rx
=
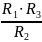 .
Такой мост
называется сбалансированным.
.
Такой мост
называется сбалансированным.
Сопротивление в работе измеряется при помощи моста постоянного тока (моста Уитстона), представленного на рисунке 1.

Рисунок 1 – мост Уитстона.
На участке АВ всегда можно найти точку D, потенциал которой равен потенциалу в точке Е: jD=je. Если между точками Е и D включен гальванометр, то в этом случае ток через него не пойдет, т.к. φe – φD= 0.
Такое состояние моста называется балансом моста. Покажем, что условие баланса определяется соотношением
|
(9) |
На основании второго закона Кирхгофа для любого замкнутого контура алгебраическая сумма падений потенциала равна алгебраической сумме электродвижущих силe:
|
(9) |
Запишем эти условия для контуров АBD и CВD в случае балансированного моста
|
(10) |
|
(11) |
Используем
первый закон Кирхгофа: алгебраическая
сумма сил токов в узле равна нулю:
 .
Узлом называется
точка или место соединения трех и более
проводников Для узла Е: IX – I+ IG =
0. При равновесии моста IG =
0, тогда получим
.
Узлом называется
точка или место соединения трех и более
проводников Для узла Е: IX – I+ IG =
0. При равновесии моста IG =
0, тогда получим ![]() ,
, ![]() .
Из (10) и (11) получим
.
Из (10) и (11) получим
|
(12) |
Деля
первое на второе, найдем соотношение
(9). Так как сопротивление изотропного
проводника цилиндрической формы зависит
от геометрических размеров и материала,
т.е.
 ,
где
,
где ![]() –
удельное сопротивление проводника; l, S –
длина и площадь сечения проводника, то
сопротивление участков АC можно записать
в виде
–
удельное сопротивление проводника; l, S –
длина и площадь сечения проводника, то
сопротивление участков АC можно записать
в виде
|
(13) |
Подставляя (13) в (9), получим искомую формулу
|
(14) |
где ![]() и
и ![]() –
длины плеч реохорда АВ; R –
сопротивление, подбираемое магазином
сопротивлений.
–
длины плеч реохорда АВ; R –
сопротивление, подбираемое магазином
сопротивлений.

ЛАБОРАТОРНАЯ РАБОТА № 8 ОБРАБОТКА РЕЗУЛЬТАТОВ
Проверка баланса моста Уитсона производится по формуле (15) в таблице 3:
Rx
=
|
(15) |
Таблица 3 – Проверка баланса моста Уитсона
2:1 |
1:1 |
1:2 |
Коаксильный кабель |
||
4480
=
4480 = 4480 |
4480
=
4480 = 4480 |
4470
=
4470 = 4470 |
Двуx проводниковая линия |
||
1724
=
1724 = 1724 |
1698
=
1698 = 1698 |
1682
=
1682 = 1682 |
2. Вывод рабочих формул.
2.1. Вывод формул для расчета коаксиального кабеля.
 ;
;
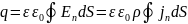 ;
;
 ;
;

 ;
;

 ;
;

 ;
;

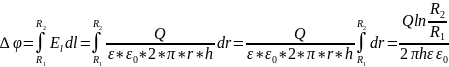
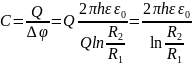
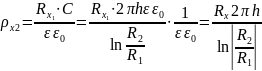
2.2. Вывод формул для расчета двух проводниковой линии.
 ;
;

;
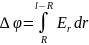
 ;
;



2.3.

3. Расчет погрешностей приведен в таблице 3.
N
= 3;
 ;
;
 ;
;
Таблица 4 – Обработка данных косвенных измерений выборочным методом
Формула |
|
|
|
4476,67 |
1701,33 |
|
3,33 |
12.24 |
|
14,32 |
52,63 |
|
33,3 |
140 |
|
43,3 |
182 |
|
0,01 |
0,8 ∙ 10-3 |
|
14,330 |
52,631 |
|
4476,67 |
1701,33 52,631 |
Вывод: В xоде работы было ознакомление с методом измерения сопротивлений при помощи моста постоянного тока для коаксильного кабеля (Rx1 = 2240 Ом; Rx2 = 4480 Ом; Rx2 = 8940 Ом); для двуx проводниковой линии (Rx1 = 862 Ом; Rx2 = 1698 Ом; Rx2 = 3364 Ом). Была произведена проверка баланса моста Уитсона. Определены удельные сопротивления материалов токопроводящих моделей (Rx1 = 4476,67 Ом ∙ м; Rx2 = 1701,33 Ом ∙ м).
Контрольные вопросы
9. Изобразите замкнутую цепь, содержащую ЭДС. Запишите закон Ома для замкнутой цепи. Какие физические величины входят в формулу и в каких единицах эти величины измеряются?
Ответ:
Замкнутая цепь, содержащая ЭДС изображена на рисунке 2.
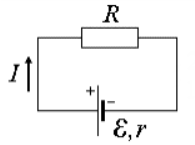
Рисунок 2 – Замкнутая цепь, содержащая ЭДС
Закон Ома для замкнутой цепи описывается формулой (10):
|
(10) |
где I – сила тока в цепи (А); R – внешнее сопротивление цепи (Ом); r – внутреннее сопротивление цепи (Ом).
14. Используя правила Кирхгофа, выведите условия баланса моста.
Ответ:
Из рисунка (1) следует, что сопротивления R1, R2, R3 и R4 образуют его «плечи». Между точками А и В моста включена батарея с э.д.с. и сопротивлением r, между точками С и D включен гальванометр с сопротивлением RG. Для узлов А, В и С, применяя первое правило Кирхгофа, получим (11):
|
(11) |
Для контуров АСВA, ACDA и CBDC, согласно второму правилу Кирхгофа, можно записать:


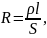
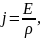


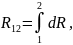




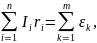
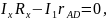

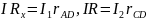



 ;
;
 ;
; ;
;
 ;
;
 ;
; ;
;
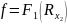

 Ом
∙ м
Ом
∙ м ,
Ом ∙ м
,
Ом ∙ м Ом
∙ м
Ом
∙ м ,
Ом ∙ м
,
Ом ∙ м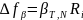 ,
Ом
∙ м
,
Ом
∙ м ,
Ом ∙ м
,
Ом ∙ м ,
Ом ∙ м
,
Ом ∙ м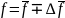 ,
Ом ∙ м
,
Ом ∙ м 14,330
14,330
