Лабораторная работа № 4 обработка результатов
Таблица 3 – Данные для контура, охватывающего один из электродов
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
2,85 |
2,96 |
3,03 |
3,13 |
3,21 |
3,33 |
3,44 |
3,55 |
3,67 |
3,77 |
3,85 |
3,99 |
4,04 |
4,18 |
4,27 |
4,44 |
|
2,92 |
3,01 |
3,08 |
3,14 |
3,24 |
3,35 |
3,46 |
3,59 |
3,69 |
3,78 |
3,88 |
4 |
4,09 |
4,21 |
4,23 |
4,47 |
|
0,07 |
0,05 |
0,05 |
0,01 |
0,03 |
0,02 |
0,02 |
0,04 |
0,02 |
0,01 |
0,03 |
0,01 |
0,05 |
0,03 |
-0,04 |
0,03 |
1) Теоретическая емкость 2-хпроводной линии.
2) Экспериментальная емкость 2-хпроводной линии
=1*10–10
Кл/м
3) Заряд электронов.
4) Энергия электрического поля 2-хпроводной линии на единицу длины.
Вывод: В
ходе работы, было проведено исследование
электростатического поля, созданного
системой проводящих тел; экспериментальное
определение электроемкости системы
проводников, определение заряда
электродов и энергии электрического
поля 2–проводной линии. Ее емкость и
энергия электрического поля очень малы.
,
что говорит о возможных неточностях
измерений при проведении опыта.
Контрольные вопросы
53. Физический смысл потенциала поля. Единицы измерения потенциала.
Ответ:
Потенциал – скалярная энергетическая характеристика электростатического поля, характеризующая потенциальную энергию, которой обладает единичный положительный пробный заряд, помещённый в данную точку поля.
Физический смысл имеет только разность потенциалов (или напряжение) между двумя какими–либо точками в электрическом поле, так как работа по переносу заряда в поле определена только тогда, когда заданы и начало, и конец этого пути переноса. Поэтому, когда мы говорим об электрическом напряжении, то всегда имеем в виду две точки, между которыми существует это напряжение.
В СИ за единицу разности потенциалов принимают вольт (В).
85. Выведите формулу для расчета потенциала внутри и вне металлического шара, заряженного зарядом q.
Ответ:
Так
как
,
тогда разность потенциалов в произвольных
точках 1 и 2:
,
следовательно,
Разность потенциалов между точками поля, образованного заряженной сферической поверхностью графически представлена на рисунке 2.
Рисунок 2 – Потенциал сферы
Разность потенциалов сферы позволяет найти разность потенциалов снаружи равномерно заряженного шара. Разность потенциалов внутри равномерно заряженного шара. Имеем диэлектрический шар, заряженный с объемной плотностью. Теперь найдем разность потенциалов внутри шара:
или
−
=−
=−
=−
или
−
=
Графическое изображение разности внутри равномерно заряженного шара представлено на рисунке 3.
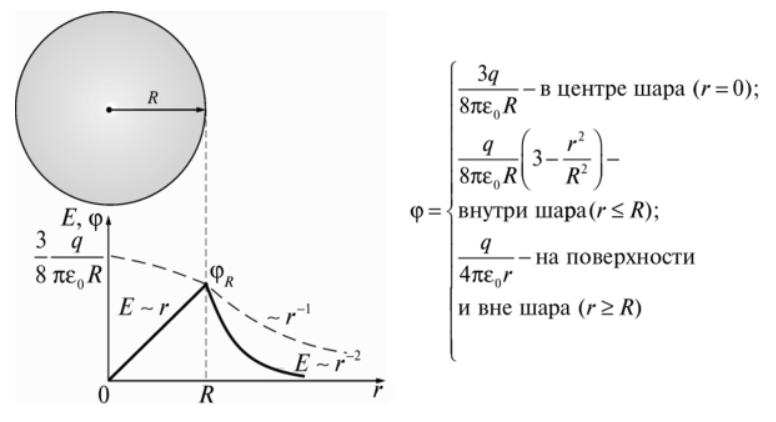
Рисунок 3 – Потенциал шара