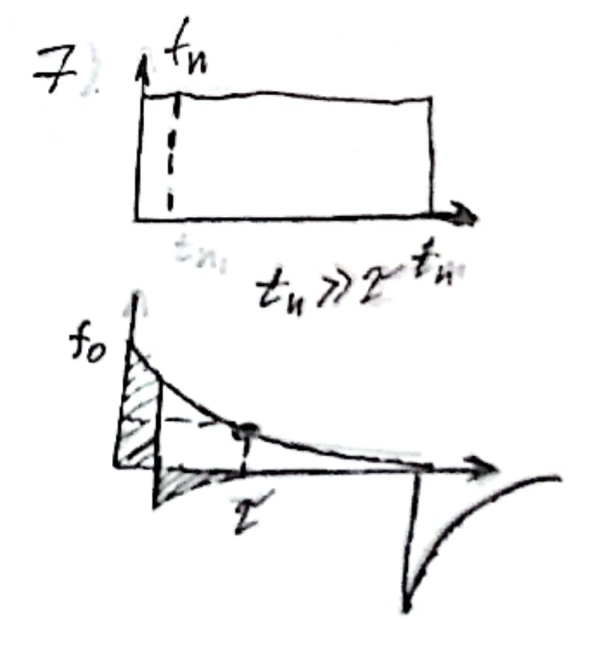
- •Глава 7, стр 160.
- •Комплексная форма записи ряда Фурье.
- •Выводы:
- •16 Февраля 2022 г.
- •Для экзамена сдача и защита кр, лаб, 2 кр, все дз.
- •Связь спектральных и частотных характеристик.
- •Формула Релея и критерии ширины спектра
- •Характеристики идеальной неискажающей интегрирующей и дифференцирующей цепи.
- •Решения для реальной дифференцирующей цепи и характеристики.
- •Трансформатор в линейном режиме.
- •§1. Вводные замечания
- •Интегральная форма первого уравнения
- •Второе уравнение Максвелла или закон электромагнитной индукции.
- •Баланс энергии электромагнитного поля.
- •Основные уравнении напряженности электрического поля.
- •Вопрос на 3.
- •7 Такая волна называется плоской.
Формула Релея и критерии ширины спектра
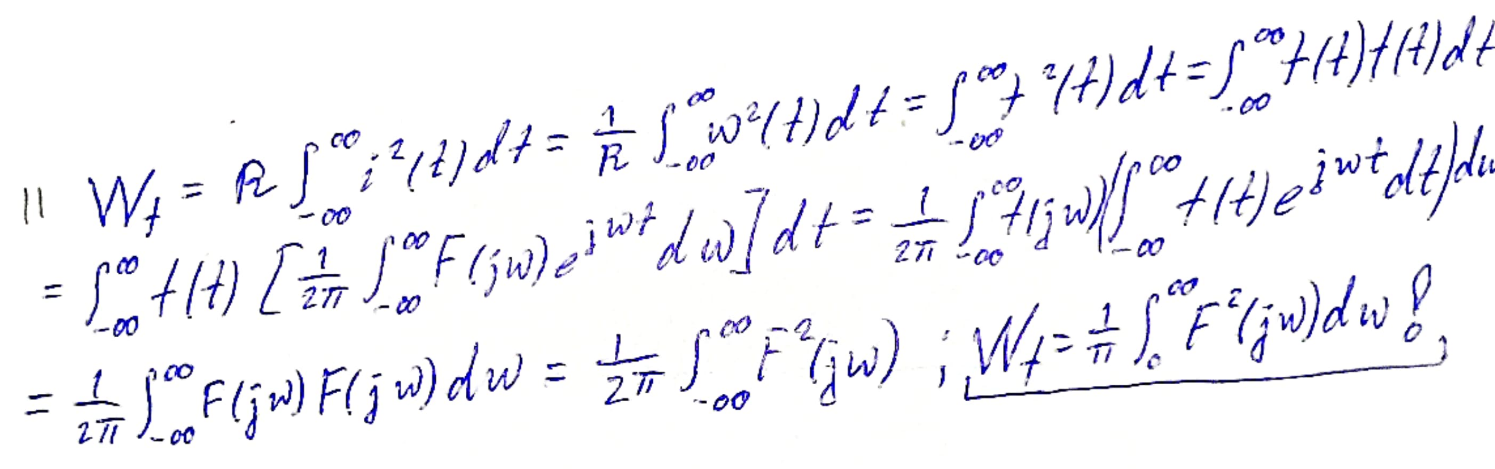
Пределы интегрирования от 0 до оо. Т.е. мы принципиально не можем определить.
Под интегралом заключен квадрат амплитудного спектра.
Для того, чтобы определить энергетический критерий ширины спектра
Энергетический критерий ширины спектра:
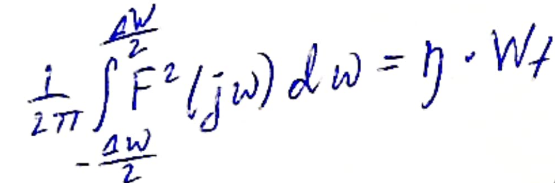
Показывает диапазон частот в который попадает какая-то часть ŋ=0,9...0,95.
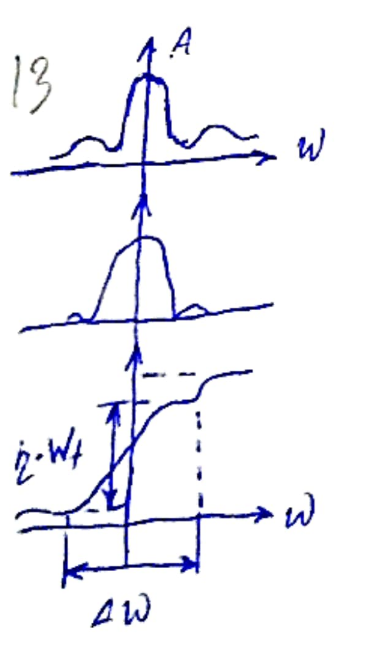
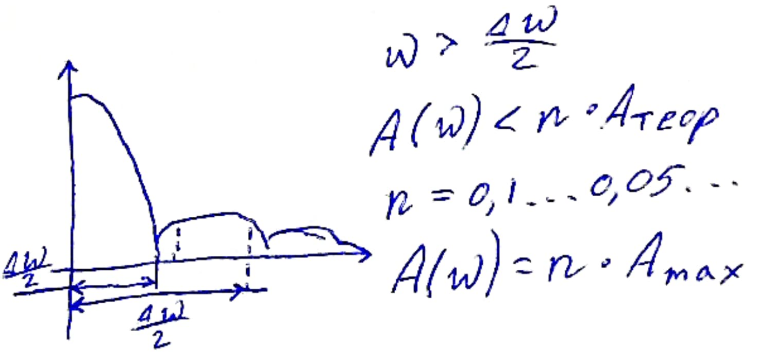
Критерий первого лепестка это когда функция превращается в 0. Самый простой пример это экспонента и для неё этот критерий не подходит.
99% сигнала не имеют критерия первого лепестка.
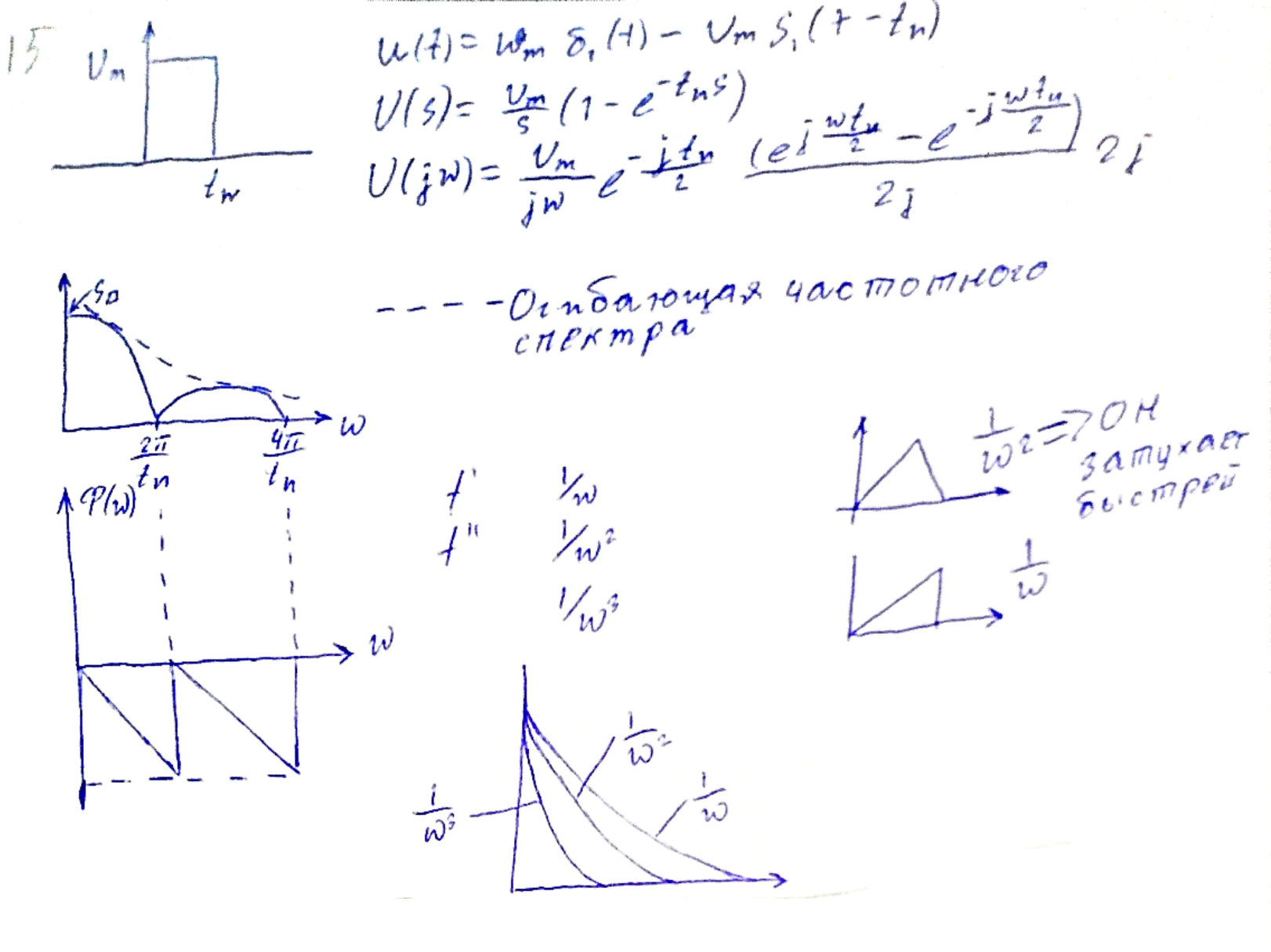
По крутизна можно судить какая производная приводит к разрыву.
Приближенный метод расчёта сигнала по его спектру
АЧХ, ФЧХ
Выбрали достаточно большой период и определили u1. Заменил неприрвыный одиночный импульс на дискретный спектр с периодом T и умножили амплитуду на

Спектральный метод расчёта электрических цепей
Представляем входной импульс в виде отрезка ряда Фурье.
Проверяем правильность выбора периода
Чтобы получить спектр выходного сигнала умножаем каждую из гормонов входного сигнала на соответствующее значение.
Значение АЧХ (0) показывает во сколько раз площадь выходного сигнала будет меньше площади входного.
Значение АЧХ на оо показывает как мгновенное изменение сигнала передаётся на выход.
Сравнивая спектр входного сигнала и ФЧХ цепи можно очень многое сказать о том, что мы увидим на выходном сигнале. Основная часть попадает в зону не искажения .
4. Характеристики идеальной неискажающей интегрирующей и дифференцирующей цепи.
9 марта 2022 г.
15:42
Характеристики идеальной неискажающей интегрирующей и дифференцирующей цепи.
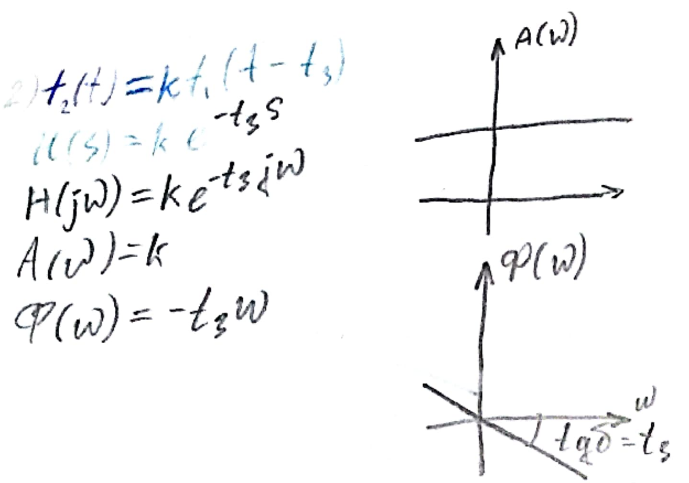
tg d - время запаздывания
При качественном анализе частотной цепи в зоне не искажения каждую частотную характеристику можно считать раной нулю.
Рассмотрим дифференцирующею цепь.
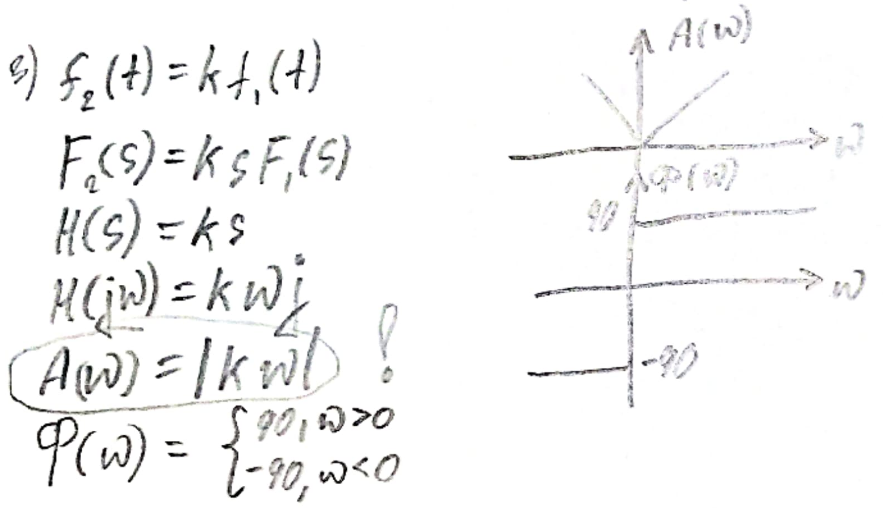
Т.к. взяли модуль амплитудного спектра.
Мы говорим о идеальной цепи, которой не существует.
Если АЧХ стремится к бесконечности? Это означает, что А оо определяет реакцию цепи на скачек, следовательно на выходе мы увидим бесконечно большой скачок.
Идеально интегрированная цепь.
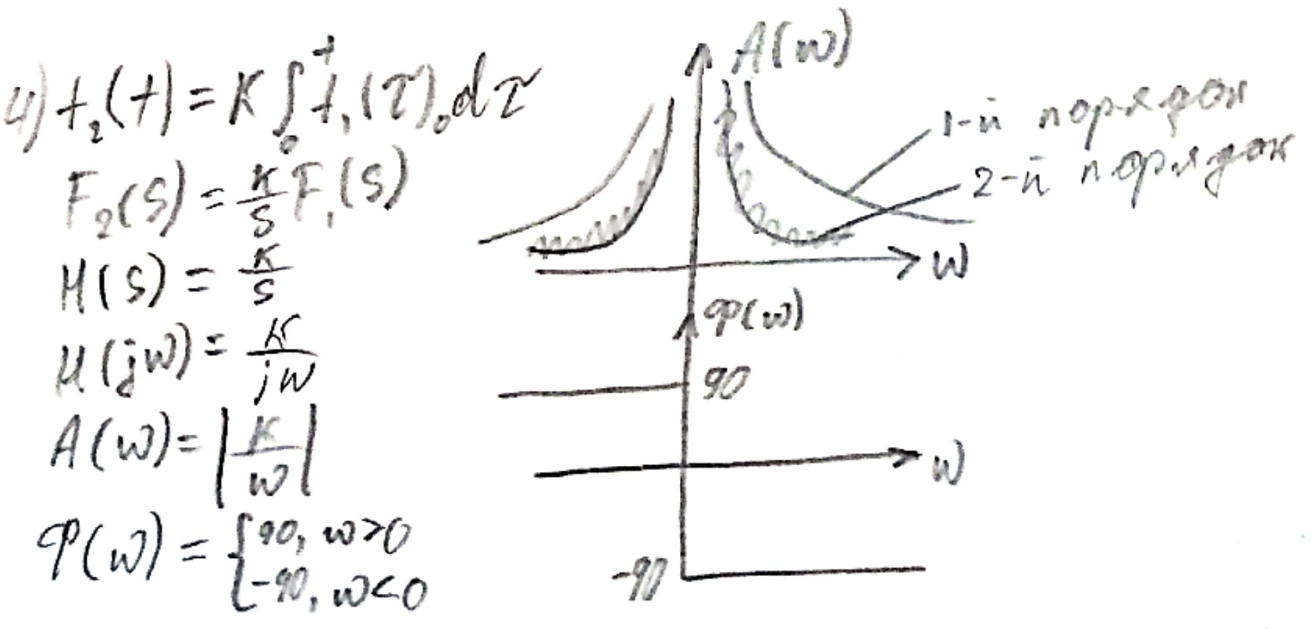
Почему интегрируются от 0? Это отсылка к НННУ и преобразованию по Лапласу.
Это идеальная цепь, поскольку на 0 частоте АЧХ устремляется к бесконечности. 0 частота отвечает за площадь сигнала.
Общее замечание:
Если дифференцирующее звено второго порядка, линейный рост знаменитая на параболу, а ФЧХ ±180.
Решения для реальной дифференцирующей цепи и характеристики.

АЧХ можно разбить на зону дифференцирования, в которой АЧХ пропорциональна частоте и на зону не искажения, где АЧХ практически горизонтальная, ФЧХ практически равна 0.
Чем больше длина импульса, тем хуже его спектр.
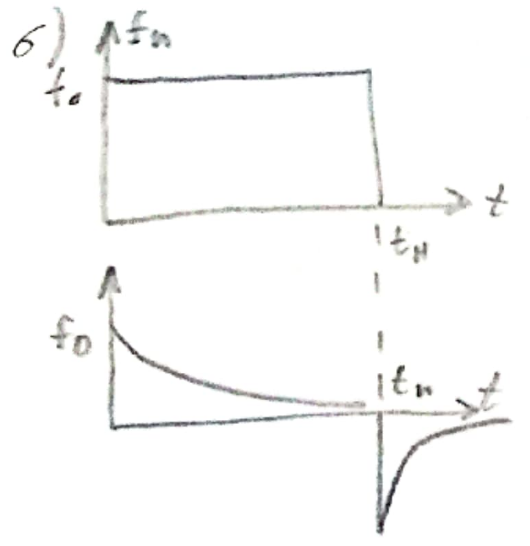
Результаты анализа для реальной дифференцирующей цепи во временной и частотной области совпадают.
Реальная интегрирующая цепь.

Частотные характеристики этой цепи разлагаются на два интервала:
Частота меняется от 1 до г. В этом интервале частотная характеристика близка к горизонтали. Характерна для зоны не искажения.
Видим падающую частотную характеристику, которая характерна для зоны интегрирования. 9
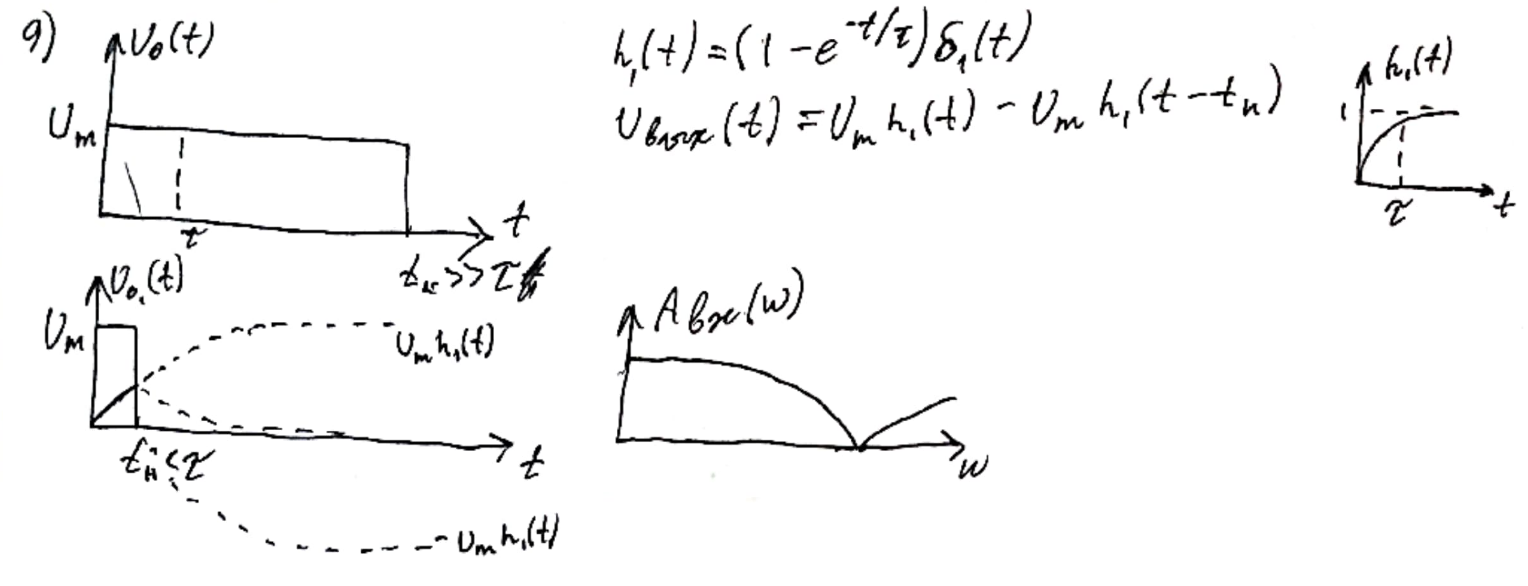
Вывод: результаты анализа во временной и частотной области совпадают.
Спектры единичной ступенчатой функции и амплитудно-модулированного сигнала.
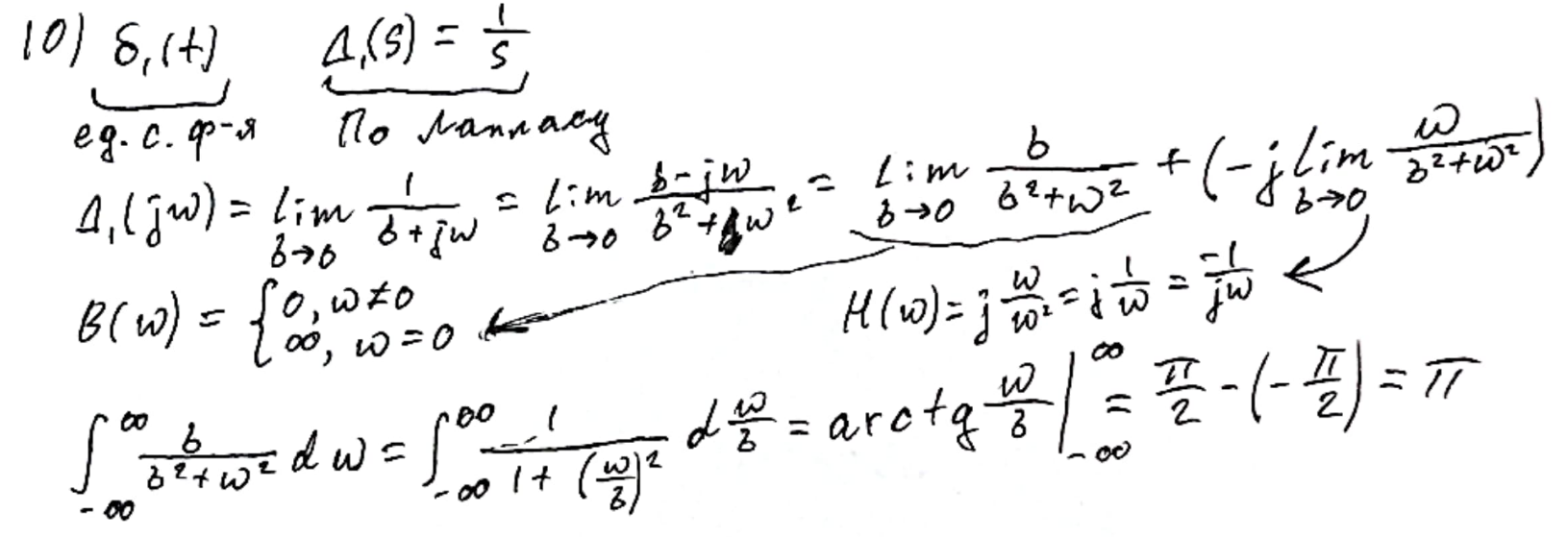
Выводы:
Для функций, корни которых находятся в левой полуплоскости преобразование по Фурье можно найти подставив преобразование по Лапласу S = ju.
Для функций, корни которой находятся на мнимой оси (не являются абсолютно интегрируемые. В частности это cos и sin) изображение по Фурье этих функций выглядит аналогичным, что мы делали для единично ступенчатой функции.
Функция, в которой есть хотя бы один корень в правой полуплоскости изображение по Фурье не имеют.
Спектры амплитудно-модулированного сигнала.
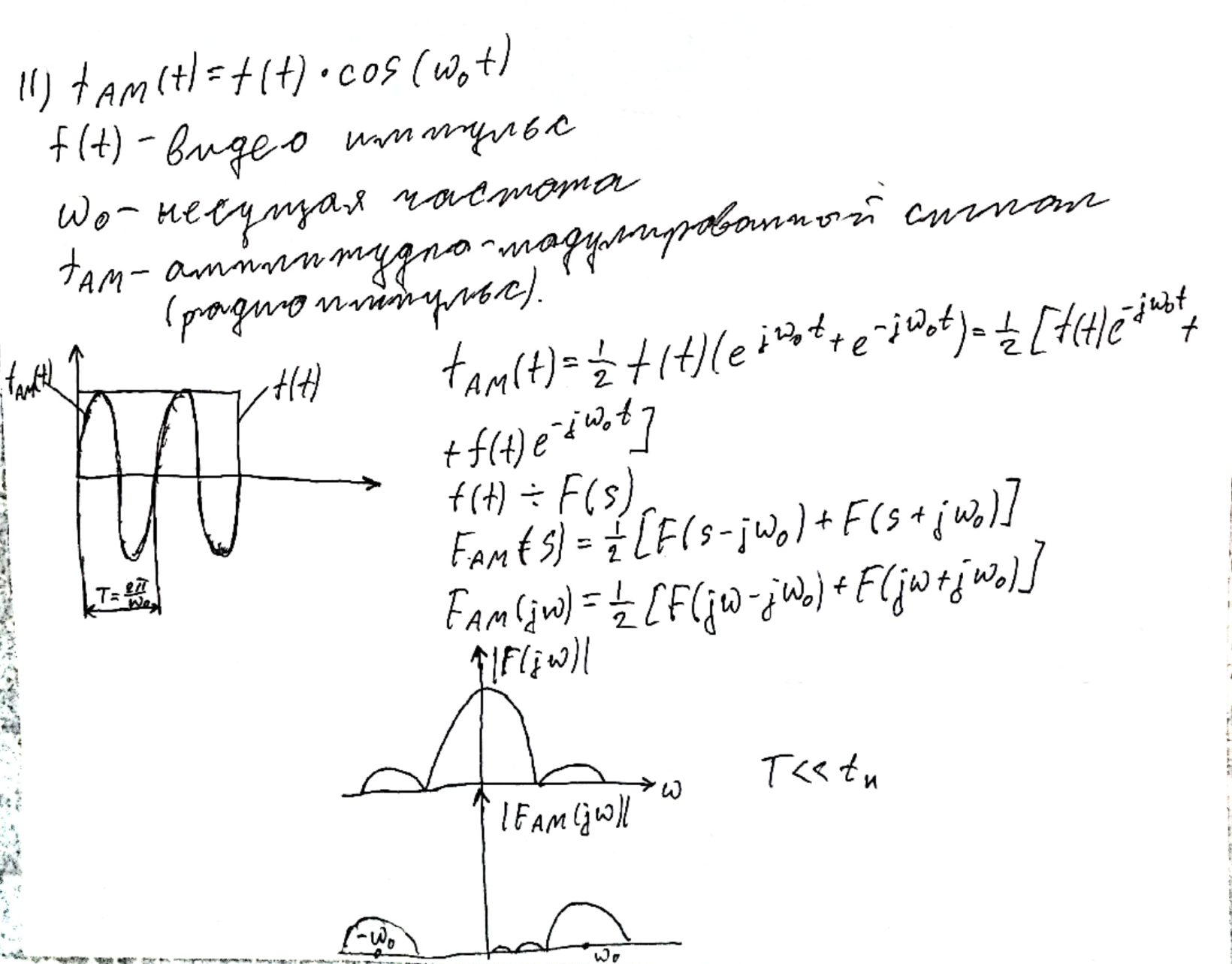
Спектр АМ сигнала повторяет форму спектра видеоимпульса, но оказывается в два раза меньше по амплитуде и сдвинут на uo и -uo.
Повторяет форму только в том случае, если период значительно меньше, чем длительность импульса хотя бы в десять раз (лучше в 100). На практике это в 10 000 раз.
5. Индуктивно-связанные цепи.
16 марта 2022 г.
15:32

n - кол-кол-во витков в катушке.
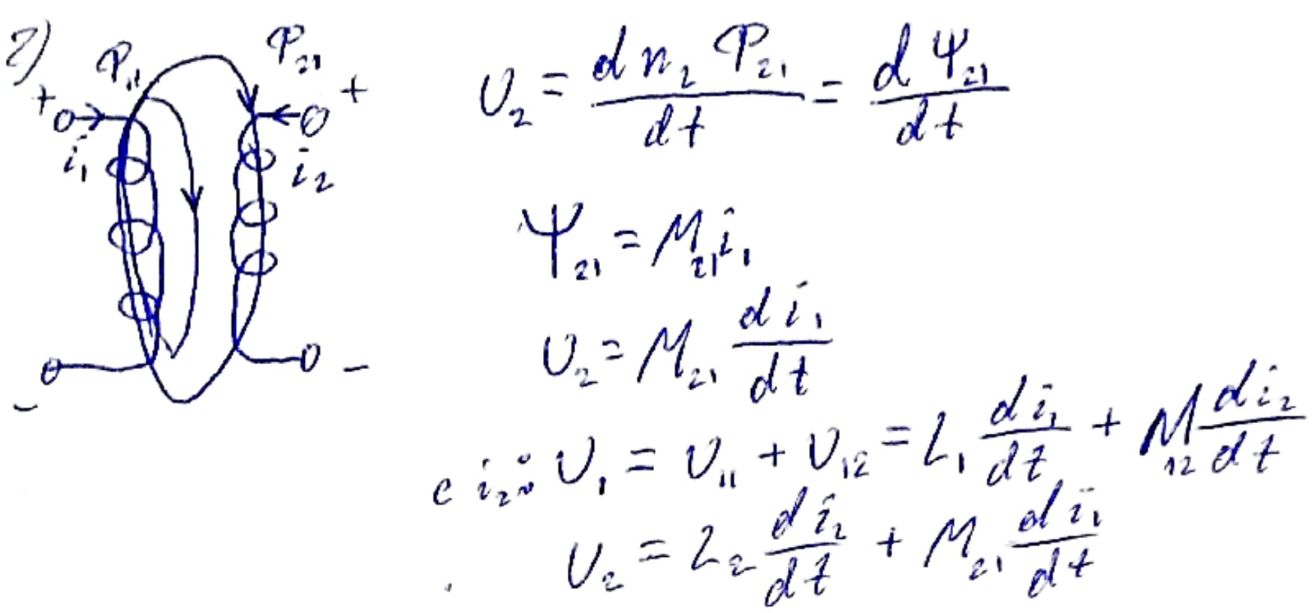
Коэффициент взаимоиндукции связан с геометрическими размерами и взаимным расположением индуктивно связанных элементов и свойствами среды, в которой они находятся.
Та часть потока fu1, которая не пересекает потоки называется потоком рассеивания Фs1.
Можно ввести понятия индуктивность рассеивания
![]()
Ф11 = Фs1 + Ф21 / n1/i
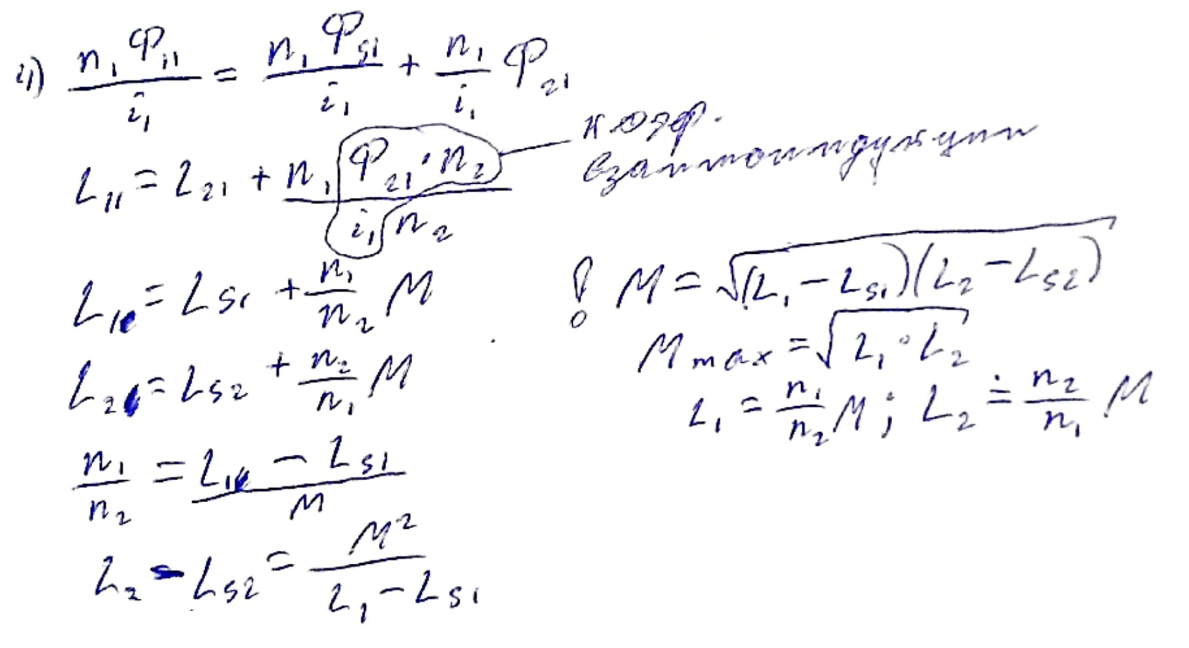
Если катушки намотаны в одном направлении, то напряжения на них будут складываться. Если в разных направления, то будет знак "-". Чтобы в этом не запутаться их отмечают *.

коэффициент связи.

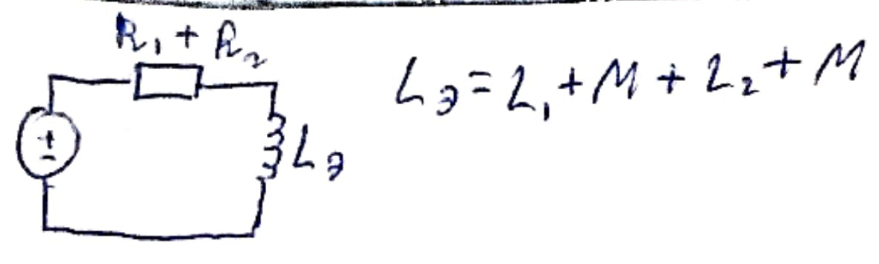


Вне зависимости от направления тока.
В случае если один со *, другой без неё, изменились бы знаки М.