В данном случае фазовые траектории представляют собой спирали. Направление закручивания спиралей можно определить по знаку коэффициента a21 в исходной матрице A. Положительный коэффициент a21 > 0
соответствует закручиванию спиралей против часовой стрелки, а при a21 <
0 спирали будут закручиваться по часовой стрелке. Как было подтверждено ранее, собственные значения матрицы системы комплексные числа, действительные части которых равны и отличны от нуля. Следовательно, такая система неустойчива.
3.1.5Неустойчивый фокус
Аналитическим путем исследуем тип особой точки в положениях рав-
новесия. 8
>x0 = 0:1x 4y
<
>y0 = 4x + 0:1y
:
Выпишем коэффициенты системы уравнений в матричной форме:
Найдем собственные значения матрицы А:
2 (a11 + a22) + a11a22 a12a21 = 0
2 (0:1 + 0:1) + (0:1)(0:1) ( 4)(4) = 0
В результате имеем следующее:
1 = 0:1 + 4i; 2 = 0:1 4i
Исходя из полученных результатов аналитически можно сделать вывод о том, что данная система представляет собой неустойчивый фокус. Построим фазовый портреты линеаризованной системы.
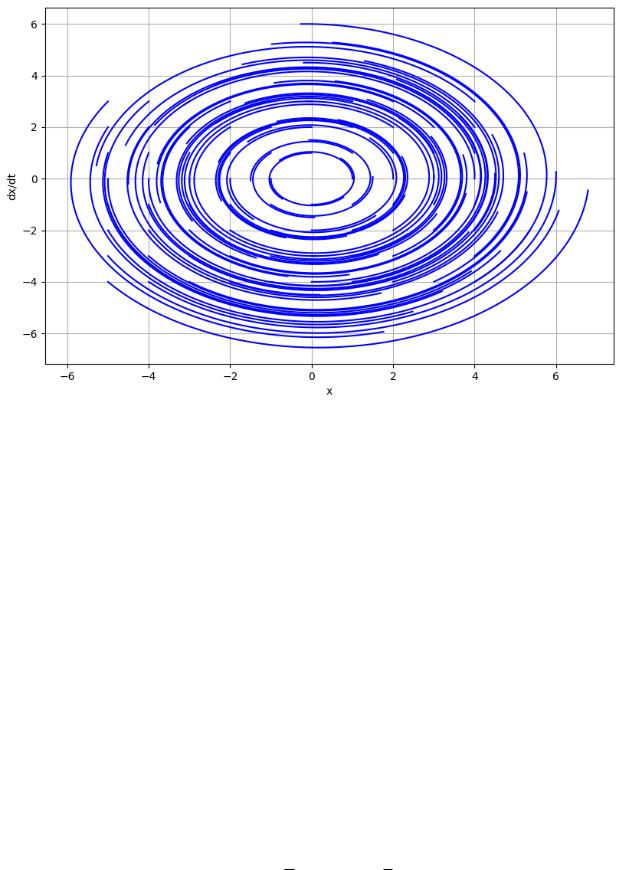
На рисунке 5 представлен фазовый портрет неустойчивого фокуса. В данном случае фазовые траектории представляют собой спирали. Направление закручивания спиралей можно определить по знаку коэффициента a21 в исходной матрице A. Положительный коэффициент a21 > 0 ñîîò-
ветствует закручиванию спиралей против часовой стрелки, а при a21 < 0
спирали будут закручиваться по часовой стрелке. Как было подтверждено ранее, собственные значения матрицы системы комплексные числа, действительные части которых равны и отличны от нуля. Следовательно, такая система неустойчива.
Рисунок 5 Фазовый портрет неустойчивого фокуса
3.1.6Центр
Аналитическим путем исследуем тип особой точки в положениях рав-
новесия. 8
>x0 = x 4y
<
>y0 = 2x y
:
Выпишем коэффициенты системы уравнений в матричной форме:
1 4 A = 2 1 :
Найдем собственные значения матрицы А:
2 (a11 + a22) + a11a22 a12a21 = 0
2 (1 1) + (1)( 1) ( 4)(2) = 0
В результате имеем следующее:
pp
1 = 7i; 2 = 7i
Исходя из полученных результатов аналитически можно сделать вывод о том, что данная система представляет собой центр. Построим фазовый портреты линеаризованной системы.