
УТС 6 семестр / Лабораторные работы / 2Лабораторная работа / lab3petrukhina
.pdfМИНОБРНАУКИ РОССИИ САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ¾ЛЭТИ¿ ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА)
Кафедра АПУ
ОТЧЕТ
по лабораторной работе №2 по дисциплине ¾Теория автоматического управления¿
Тема: Метод фазового пространства Вариант №19
Студент(ка) гр. 6392 |
|
Петрухина Т.С. |
Преподаватель |
|
Синица А.М. |
Санкт-Петебург
2019
Содержание
1. |
Цель работы |
3 |
2. |
Основные теоретические положения |
3 |
3. |
Обработка результатов эксперимента |
4 |
|
3.1. Построение фазовых портретов для типовых особых точек . . . |
4 |
|
3.2. Построение фазовых портретов для нелинейных систем . . . . . |
9 |
|
3.3. Построение фазового портрета для маятника . . . . . . . . . . . |
10 |
|
3.4. Построение фазового портрета осциллятора Ван дер Поля . . . |
12 |
|
3.5. Построение фазового портрета аттрактора Лоренца (3 порядок) |
15 |
4. |
Вывод |
16 |
2
1. Цель работы
Знакомство с особенностями метода фазового пространства.
2. Основные теоретические положения
Метод фазовой плоскости дает возможность изобразить качественную картину всей совокупности свободных движений (процессов) для выбранной области начальных условий (состояний), а при необходимости провести точные исследования интересующих типов движений. Через каждую точку фазового пространства при условии однозначности функции проходит только одна фазовая траектория. Единственность нарушается в особых точках, соответствующих точкам равновесия. Существует несколько основных типов особых точек (типов поведения в окрестности положения равновесия):
-устойчивый узел -неустойчивый узел -седло -устойчивый фокус
-неустойчивый фокус -центр
Заметим также, что особые точки являются частным случаем аттракторов компактных подмножеств фазового пространства динамической системы, все траектории из некоторой окрестности которого стремятся к нему при времени, стремящемся к бесконечности. Кроме особых точек (точек равновесия) аттрактором могут быть замкнутые траектории (предельные циклы) или некоторая ограниченная область с неустойчивыми траекториями внутри (как у странного аттрактора).
3
3. Обработка результатов эксперимента
3.1.Построение фазовых портретов для типовых особых точек
Построим фазовые портреты следующих систем для анализа поведения решений в окрестности особых точек, используя Jupiter Notebook на языке Python. Займемся рассмотрением типов особых точек линейных систем второго порядка, в зависимости от расположения корней характеристического полинома.
1. Устойчивый узел
8
<x0 = 4x 4y
:y0 = 1:5x + y
Код системы уравнений на языке Python:
def ode(Y, t, b, c): x, y = Y
dydt = [-4*x-4*y, 1.5*x+y] return dydt
drawPhasePortrait(args, 1, 1, -5, 5, -4, 4, ts = 0.5, nt = 301)
На рисунке 1 можно заметить, что все линии фазовых траекторий стремятся к одной точке (0;0). Для места типа "устойчивый узел"характерны действительные отрицательные корни характеристического полинома. Прямолинейным фазовым траекториям соответствуют состояния, когда постоянные при одной из экспонент равняются нулю.
2. Неустойчивый узел Ниже представлена система уравнений "неустойчивый узел".
8
<x0 = x + 0:5y
:y0 = 0:5x + y
Код системы уравнений на языке Python: 4
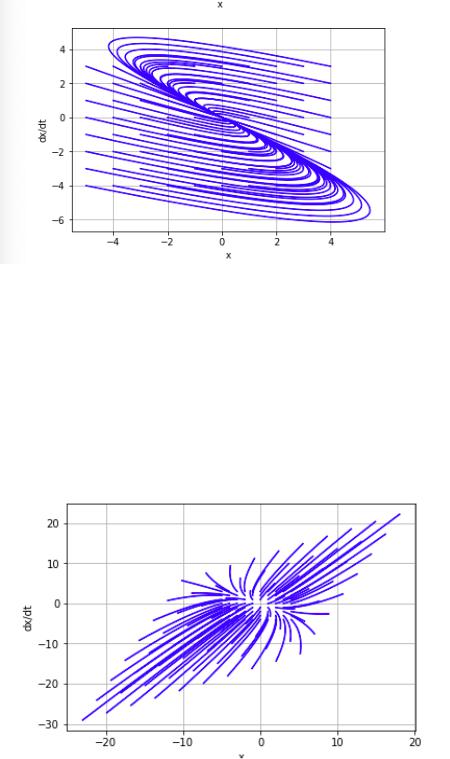
Рис. 1. Фазовый портрет устойчивого узла
def ode(Y, t, b, c): x, y = Y
dydt = [x+0.5*y, 0.5*x+y] return dydt
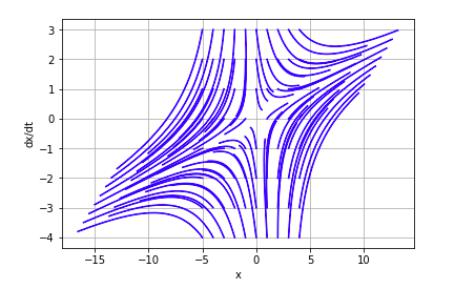
Рис. 2. Фазовый портрет неустойчивого узла
При положительных действительных корнях имеем особую точку типа "неустойчивый узел"(рисунок 2). В данном случае можно наблюдать рассосредоточение линий фазовых траекторий вокруг центра координат. Они не достигают точки (0;0).
3. Седло
5
Ниже представлена система уравнений "седло".
8
<x0 = 2x + y
:y0 = x 3y
Код системы уравнений на языке Python:
def ode(Y, t, b, c): x, y = Y
dydt = [2*x+y, x-3*y] return dydt
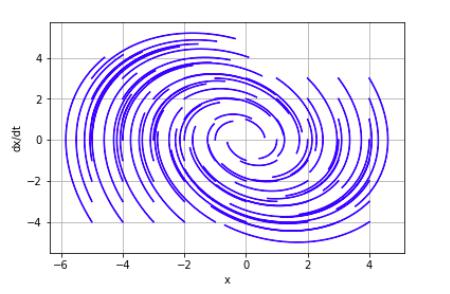
Рис. 3. Фазовый портрет седла
Как и в случае с "неустойчивым узлом"фазовый портрет "седла"(рисунок 3) не имеет пересечний центра координат (0;0). Имеются прямолинейные траектории - сепаратрисы седла, которые соответствуют случаю, когда один из коэффициентов характеристического полинома равен нулю. Также, седло получается когда один корень отрицательный, а другой положительный.
4. Устойчивый фокус
8
<x0 = 2y
:y0 = 3x y
Код системы уравнений на языке Python: 6
def ode(Y, t, b, c): x, y = Y
dydt = [2*y, -3*x-y] return dydt
Рис. 4. Фазовый портрет устойчивого фокуса
На рисунке 4 запечатлены закругленные линии фазовых траекторий, которые стремятся к центру системы координат. Такое положение линий сохраняется, если имеются комплексно-сопряженные корни с отрицательными действительными частями.
5. Неустойчивый фокус Ниже представлена система уравнений "неустойчивый фокус".
8
<x0 = 0:1x 4y
:y0 = 4x + 0:1y
Код системы уравнений на языке Python:
def ode(Y, t, b, c): x, y = Y
dydt = [0.1*x-4*y, 4*x+0.1*y] return dydt
7
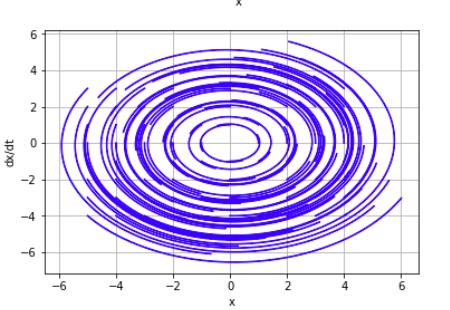
Рис. 5. Фазовый портрет неустойчивого фокуса
Если действительные части комплексных корней положительны, то имеем "неустойчивый фокус"(рисунок 5) и колебательные расходящиеся процессы.
6. Центр Ниже представлена система уравнений "центр".
8
<x0 = x 4y
:y0 = 2x y
Код системы уравнений на языке Python:
def ode(Y, t, b, c): x, y = Y
dydt = [x-4*y, 2*x-y] return dydt
На рисунке 6 представлен незатухающий колебательный процесс. Здесь можно наблюдать замкнутые элипсы с увеличивающимся радиусом, и отстутвие пересечений координатного центра.
8
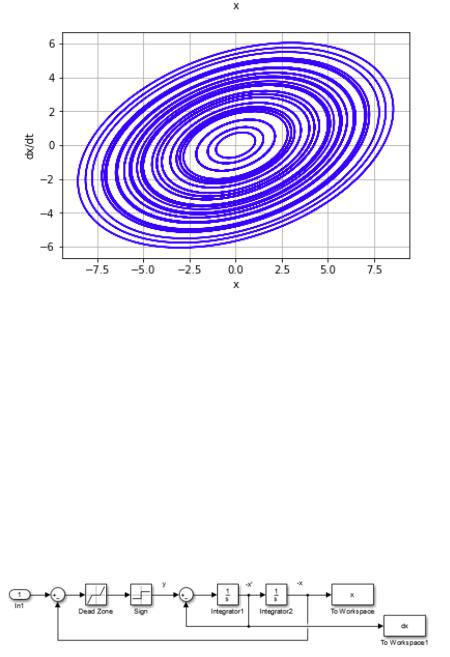
Рис. 6. Фазовый портрет центра
3.2.Построение фазовых портретов для нелинейных систем
По модели в виде блок-схемы постройте системы дифференциальных уравнений (в математической записи вместо нелинейных блоков можно определить соответствующие функции без их раскрытия). Значения параметров нелинейностей принять за 1.
Рис. 7. Блок-схема
В результате математического анализа блок-схемы получилась следующая математическая модель типа "реле с зоной нечувствительности":
def ode(Y, t, b, c): x, y = Y
dydt = [y, np.sign*(dead_zone(1 - x)) - y ] return dydt
Функция для "мертвой зоны":
9
def dead_zone_scalar(x, w=1): if np.abs(x) < w:
return 0 elif x > 0: return x-w else: return x+w
dead_zone = np.vectorize(dead_zone_scalar, otypes=[np.float])
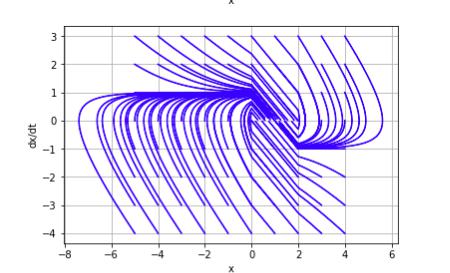
Рис. 8. Фазовый портрет нелинейной системы
На рисунке 8 можно обнаружить, что процесс разбит на ряд интервалов. Это происходит из-за переключения релейного элемента. На фазовой плоскости каждому линейному участку такой характеристики нелинейного элемента соответствует отдельная область, в пределах которой правые части дифференциальных уравнений линейны, а фазовые траектории составлены из дуг траекторий линейных систем.
3.3. Построение фазового портрета для маятника
Постройте фазовый портрет математического маятника.
10
