7.3.2. Исследование резонанса токов и ачх контура с большими потерями

Соберите схему, изображенную на рис. 7.9.

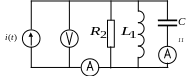
Рис. 7.9

Потери в цепи определяются проводимостью . Методика исследования такая же, как в 7.3.1. Результаты измерений занесите в таблицы, аналогичные табл. 7.3 и 7.4. Поскольку АЧХ цепи является более плавной, рекомендуется в диапазонах 8…12 кГц и 16…20 кГц изменять частоту через 2 кГц. По результатам измерений в табл. 7.3 вычислите лишь , и .

7.3.3. Исследование влияния изменения емкости на характеристики контура

Соберите схему, изображенную на рис. 7.10.

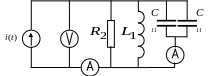
Рис. 7.10

Проведите измерения, аналогичные 7.3.2. Результаты измерений занесите в таблицы, аналогичные табл. 7.3 и 7.4. Поскольку АЧХ цепи является более плавной, рекомендуется в диапазоне 1…4 кГц изменять частоту через 1 кГц, в диапазоне 4…10 кГц через 0,5 кГц, а в диапазоне 10…18 кГц через 2 кГц.

7.4. Требования к отчету

В отчете должны быть отражены цель работы, все пункты экспериментального исследования и заключение с краткими выводами. По каждому пункту в отчет следует включить его название, схемы исследуемых цепей, таблицы измерений и вычислений, а также необходимые расчеты.

Рекомендуется на одном графике построить все АЧХ по 7.2.1 – 7.2.3 и графически рассчитать добротности, на другом – аналогично по 7.3.1 – 7.3.3. Необходимо также письменно ответить на следующие вопросы:

1. Как, используя эквивалентные схемы цепи для , и , определить значения АЧХ на этих частотах и проконтролировать результаты эксперимента? Приведите схемы замещения для этих частот.

2. В чем сходство и в чем различие данных, измеренных и рассчитанных в 7.2.1 и 7.2.2?

3. В чем сходство и в чем различие данных 7.2.2 и 7.2.3? Почему диапазон изменения частоты иной?

4. Как, используя эквивалентные схемы цепи для , и , определить значения АЧХ на этих частотах и проконтролировать результаты эксперимента?

5. В чем сходство и в чем различие данных, измеренных и рассчитанных в 7.3.1 и 7.3.2?

6. В чем сходство и в чем различие данных 7.3.1 и 7.3.2? Почему диапазон изменения частоты иной?

Работа № 9 исследование индуктивно связанных цепей

Цель работы: экспериментальное определение параметров двух индуктивно связанных катушек и проверка основных соотношений индуктивно связанных цепей при различных соединениях катушек.

9.1. Подготовка к работе

Схема замещения двух индуктивно связанных катушек, удовлетворительно учитывающая электромагнитные процессы в диапазоне низких и средних частот, представлена на рис. 9.1, где L₁, R₁ и L₂, R₂ – индуктивности и сопротивления соответственно первой и второй катушек; M – их взаимная индуктивность.

Степень магнитной связи двух катушек определяется коэффициентом связи:

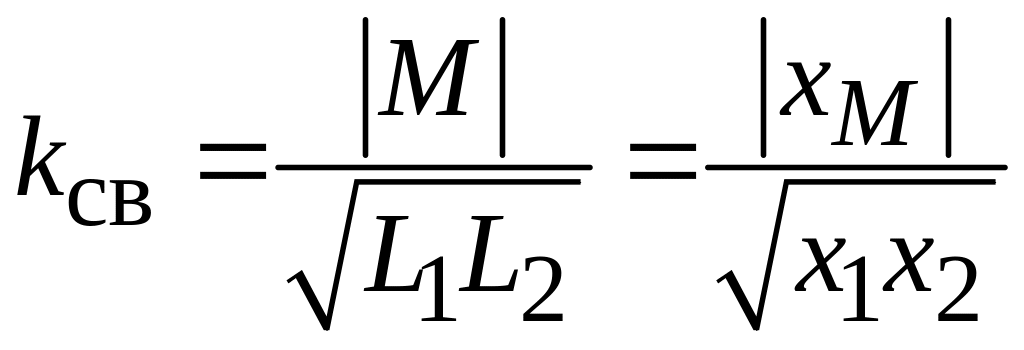, (9.1)

где , – индуктивные сопротивления катушек; – – сопротивление взаимной индуктивности, при этом 0   1.

Рис. 9.1

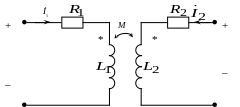
В режиме гармонических колебаний уравнения цепи на рис. 9.1 имеют вид:

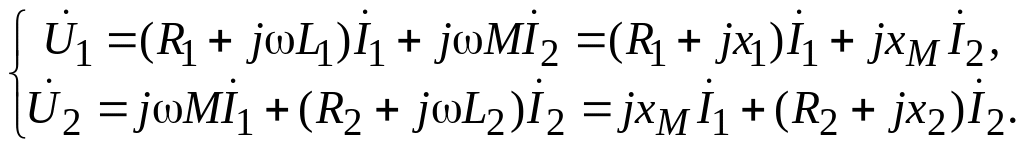(9.2)

Знак M и определяется выбором положительных направлений токов и . Для выбранных направлений токов M > 0, если включение катушек согласное, и M < 0, если включение встречное. Способ включения катушек устанавливается с помощью однополярных выводов, отмеченных «звездочками»: если токи катушек направлены одинаково относительно однополярных выводов (например, как показано на рис. 9.1), то катушки включены согласно; в противном случае включение встречное.

Параметры уравнения (9.2) могут быть определены из двух опытов холостого хода, в одном из которых I₂ = 0, в другом I₁ = 0; осуществляют эти опыты размыканием соответствующей пары внешних выводов катушек. Если используют катушки достаточно высокой добротности (L >> R), то при определении их индуктивности допустимо пренебречь активными сопротивлениями обмоток катушек, т. е. считать R₁ = 0 и R₂ = 0; ошибка при этом будет несущественной с точки зрения инженерной практики. Полагая в уравнениях (9.2) сначала I₂ = 0, а затем I₁ = 0, при условии R₁ = R₂ = 0 получаем соответственно:

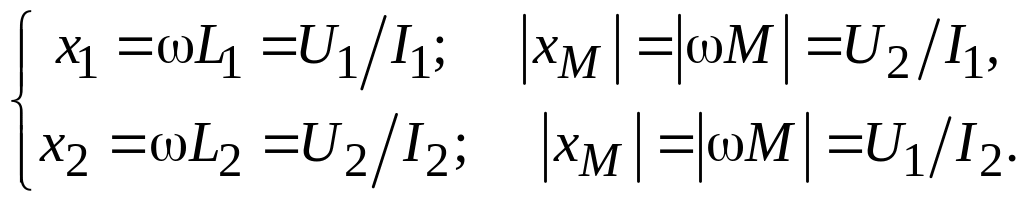(9.3)

На рис. 9.2, а показано последовательное соединение двух индуктивно связанных катушек. В этом случае , и из уравнения (9.2) при R₁ = R₂ = 0 находим выражение эквивалентной индуктивности:

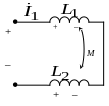. (9.4)

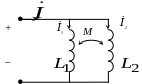
Рис. 9.2

Для параллельного соединения (рис. 9.2, б) , . Разрешая систему уравнений (9.2) относительно токов с учетом R₁ = R₂ = 0, можно получить выражение эквивалентной индуктивности:

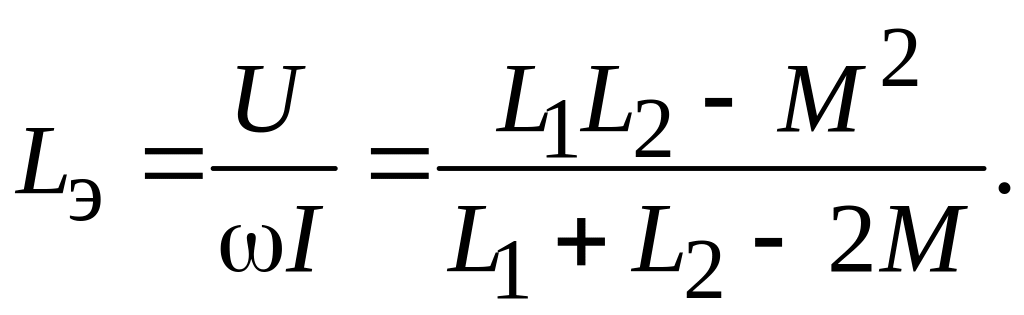(9.5)

В выражениях (9.4), (9.5) M > 0 при согласном и M < 0 при встречном включении катушек.

Если к выводам второй катушки присоединить нагрузочное сопротивление Z_н, получим двухобмоточный трансформатор (рис. 9.3). В трансформаторе энергия от источника, включенного в цепь первичной обмотки, передается нагрузке Z_н, подключенной к вторичной обмотке. Эта передача осуществляется без электрической связи между обмотками посредством изменяющегося потока взаимной индукции.

Рис. 9.3

Рассматривая трансформатор как четырехполюсник, можно его передающие свойства характеризовать функциями передачи напряжений и токов. Положив , из уравнений (9.2) при R₁ = R₂ = 0 получаем:

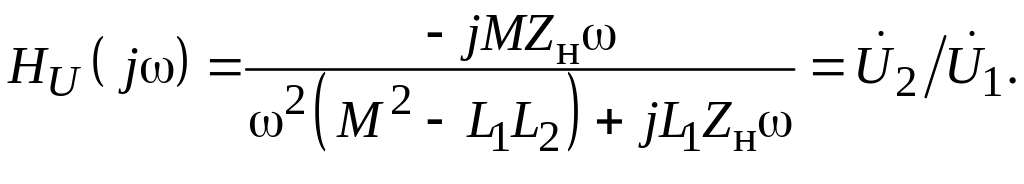(9.6)

В случае активной нагрузки (Z_н = R_н) модуль функции передачи (9.6) по напряжению (АЧХ)

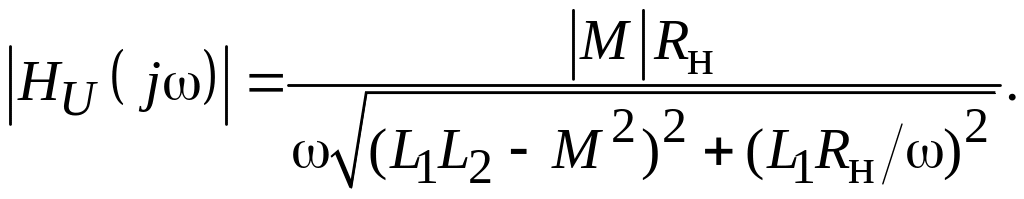(9.7)