МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра ТОЭ

отчет

по лабораторной работе №9

по дисциплине «Теоретические основы электротехники»

Тема: Исследование индуктивно связанных цепей

Студент гр. 8391		Орещенко Н.В.
Преподаватель		Завьялов А.Е.

Санкт-Петербург

2020

Цель работы.

Экспериментальное определение параметров двух индуктивно связанных катушек и проверка основных соотношений индуктивно связанных цепей при различных соединениях катушек.

Основные теоретические положения.

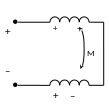
Схема замещения двух индуктивно связанных катушек, удовлетворительно учитывающая электромагнитные процессы в диапазоне низких и средних частот, представлена на рис. 9.1, где L₁, R₁ и L₂, R₂ – индуктивности и сопротивления соответственно первой и второй катушек; M – их взаимная индуктивность.

Степень магнитной связи двух катушек определяется коэффициентом связи:

, (9.1)

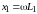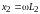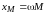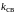
где , – индуктивные сопротивления катушек; – – сопротивление взаимной индуктивности, при этом 0   1.

Рис. 9.1

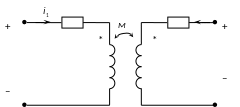
В режиме гармонических колебаний уравнения цепи на рис. 9.1 имеют вид:

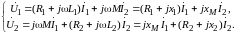(9.2)

Знак M и 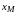определяется выбором положительных направлений токов 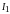и 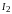. Для выбранных направлений токов M > 0, если включение катушек согласное, и M < 0, если включение встречное. Способ включения катушек устанавливается с помощью однополярных выводов, отмеченных «звездочками»: если токи катушек направлены одинаково относительно однополярных выводов (например, как показано на рис. 9.1), то катушки включены согласно; в противном случае включение встречное.

Параметры уравнения (9.2) могут быть определены из двух опытов холостого хода, в одном из которых I₂ = 0, в другом I₁ = 0; осуществляют эти опыты размыканием соответствующей пары внешних выводов катушек. Если используют катушки достаточно высокой добротности (L >> R), то при определении их индуктивности допустимо пренебречь активными сопротивлениями обмоток катушек, т. е. считать R₁ = 0 и R₂ = 0; ошибка при этом будет несущественной с точки зрения инженерной практики. Полагая в уравнениях (9.2) сначала I₂ = 0, а затем I₁ = 0, при условии R₁ = R₂ = 0 получаем соответственно:

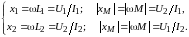(9.3)

На рис. 9.2, а показано последовательное соединение двух индуктивно связанных катушек. В этом случае 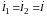, 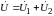и из уравнения (9.2) при R₁ = R₂ = 0 находим выражение эквивалентной индуктивности:

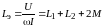. (9.4)

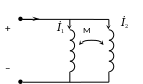
Рис. 9.2

Для параллельного соединения (рис. 9.2, б) 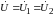, 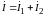. Разрешая систему уравнений (9.2) относительно токов с учетом R₁ = R₂ = 0, можно получить выражение эквивалентной индуктивности:

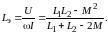(9.5)

В выражениях (9.4), (9.5) M > 0 при согласном и M < 0 при встречном включении катушек.

Если к выводам второй катушки присоединить нагрузочное сопротивление Z_н, получим двухобмоточный трансформатор (рис. 9.3). В трансформаторе энергия от источника, включенного в цепь первичной обмотки, передается нагрузке Z_н, подключенной к вторичной обмотке. Эта передача осуществляется без электрической связи между обмотками посредством изменяющегося потока взаимной индукции.

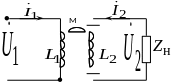
Рис. 9.3

Рассматривая трансформатор как четырехполюсник, можно его передающие свойства характеризовать функциями передачи напряжений и токов. Положив 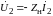, из уравнений (9.2) при R₁ = R₂ = 0 получаем:

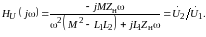(9.6)

В случае активной нагрузки (Z_н = R_н) модуль функции передачи (9.6) по напряжению (АЧХ)

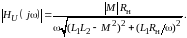(9.7)

Протокол наблюдений

							Таблица 9.1
Номер катушки	Наблюдают			Вычисляют
	U1, B	U2, B	I, мА	x, Ом	L, Гн	|xM|, Ом	|M|, Гн
1	2	1.304	0,414
2	1.427	2	0,453

									Таблица 9.2
Включение	Наблюдают				Вычисляют
	U, B	U1, B	U2, B	I, мА		I, мА	U1, B	U2, B	Lэ, Гн
Согласное	2	1,04	0,965	0,131
Встречное	2	0,977	1,126	0,524

				Таблица 9.3
Включение	Наблюдают		Вычисляют
	U, B	I, мА	I, мА	Lэ, Гн
Согласное	1	0,51
Встречное	1	2,039

						Таблица 9.4
f, кГц	Нагрузка RH1			Нагрузка RH2
	Измеряют		Вычисляют	Измеряют		Вычисляют
	A(w)	Ф(w)	Hu(jw)	A(w)	Ф(w)	Hu(jw)
0,1	0,283595	64,748		0,278391	64,569
1	0,650607	11,789		0,636774	10,818
3	0,663364	3,741		0,648202	0,975
6	0,664583	1,399		0,646638	-4,099
9	0,664765	0,401		0,642254	-7,828
12	0,664775	-0,245		0,636116	-11,105
18	0,664630	-1,221		0,619162	-17,114
30	0,664028	-2,727		0,573727	-27,750
50	0,662278	-4,974		0,485458	-41,511
100	0,654193	-10,24		0,317727	-60,653
500	0,491160	-42,366		0,072472	-83,582

Обработка результатов эксперимента