
УТС 4 семестр / 3лаба
.docxМИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра ТОЭ
отчет
по лабораторной работе №3
по дисциплине «ТОЭ»
Тема: Исследование свободных процессов в электрических цепях
Студент гр. 8391 |
|
Орещенко Н.В. |
Преподаватель |
|
Завьялов А.Е. |
Санкт-Петербург
2020
Цель работы.
Изучение связи между видом свободного процесса в электрической цепи и расположением ее собственных частот (корней характеристического уравнения) на комплексной плоскости; экспериментальное определение собственных частот и добротности RLC-контура по осциллограммам.
Основные теоретические положения.
В работе предлагается исследовать свободные процессы в цепях, схемы которых представлены на рис. 3.1. Цепи возбуждаются короткими импульсами тока it0, заряжающими конденсатор C. В паузах между импульсами конденсатор разряжается; цепь находится в свободном режиме, так как в это время источник возбуждения отключен i0 0 . Напряжения на элементах цепи осциллографируются. Поведение линейных цепей описывается линейными дифференциальными уравнениями; при этом вид свободного процесса определяется корнями k p характеристического уравнения (собственными частотами цепи).
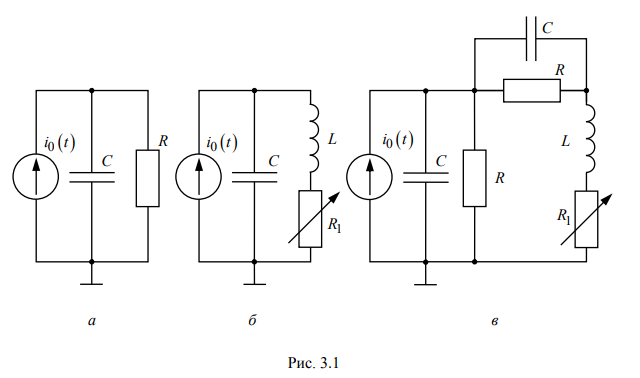
При возбуждении цепи источником тока собственные частоты можно рассчитать как нули входной проводимости цепи Y p , т. е. как корни уравнения Y p 0. Для цепи первого порядка, представленной на рис. 3.1, а, Y p pC R 1 , откуда
![]()
Для цепи второго порядка, изображенной на рис. 3.1, б, Y p pC pL R 1 1 , откуда
![]()
Для цепи третьего порядка, представленной на рис. 3.1, в,
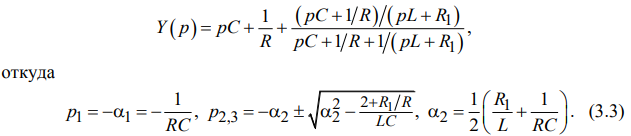
У цепи первого порядка одна собственная частота 1 p в (3.1), вещественная и отрицательная; свободный процесс описывается затухающей экспонентой:
![]()
где u – напряжение на каком-либо элементе цепи; t – время; α – постоянная затухания; τ – постоянная времени; A – постоянная интегрирования. Временная диаграмма свободного процесса приведена на рис. 3.2, а, причем τ – интервал времени, соответствующий любой подкасательной к экспоненте. У цепи второго порядка две собственные частоты 1,2 p в (3.2) могут быть вещественными (простыми или кратными) или комплексно-сопряженными. В случае вещественных простых собственных частот
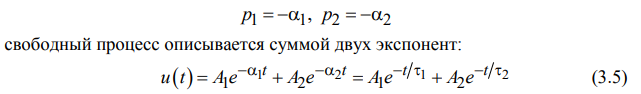

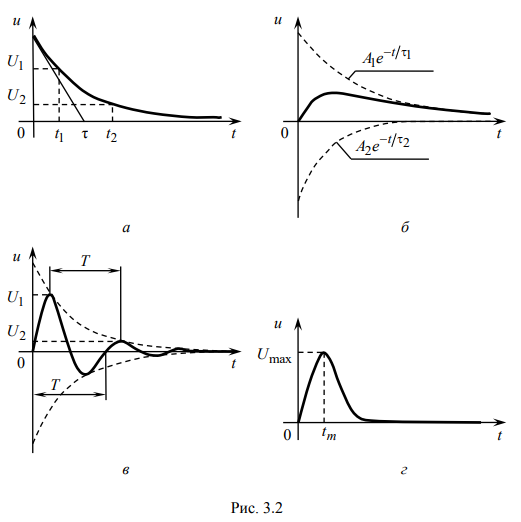

свободный процесс описывается выражением
![]()



Протокол наблюдений.

Обработка результатов эксперимента.
3.2.1. Исследование свободных процессов в цепи первого порядка
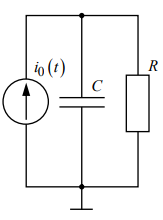
R = 5 кОм
C = 0.02 мкФ
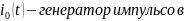
Фото 1.
Определим собственную частоту цепи:
Теоретический расчёт
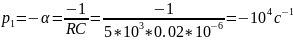
Расчёт по осциллограмме:
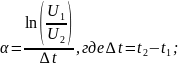
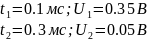
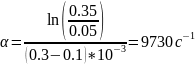
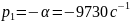
Вопросы:
1. Каким аналитическим выражением описывается осциллографируемый процесс? 2. Соответствует ли найденная собственная частота теоретическому расчету, выполненному согласно (3.1)?
Ответы:
Осциллографируемый процесс описывается аналитической формулой:
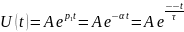
Найденная по осциллограмме собственная частота практически совпадает с теоретически рассчитанной. (теор
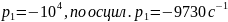 )
)
3.2.2. Исследование свободных процессов в цепи первого порядка
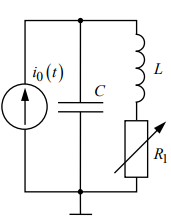
С = 0.02 мкФ
L = 25 мГн
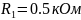 (колебательный
режим, Фото 2)
(колебательный
режим, Фото 2)Теоретический расчёт:
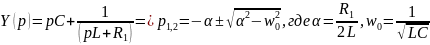
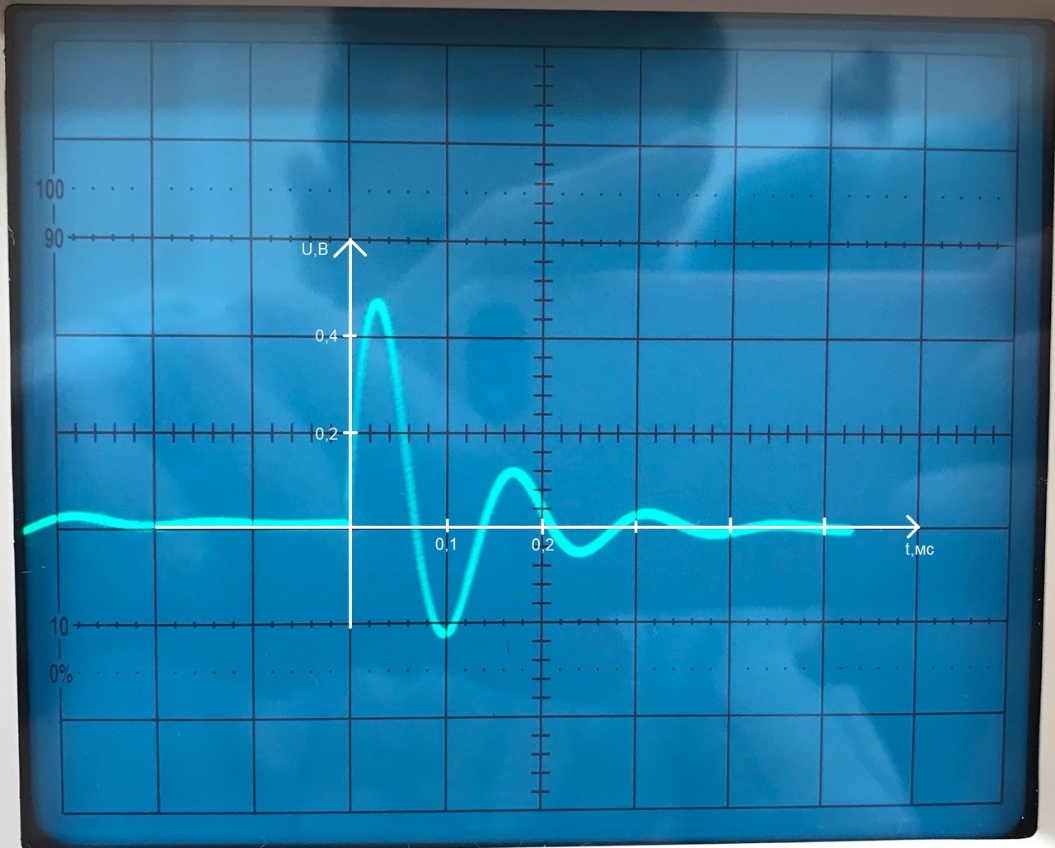
Фото 2.
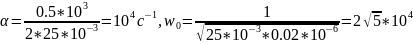
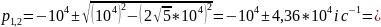
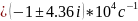
Расчёт по осциллограмме:
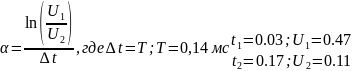
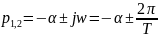
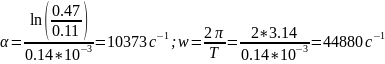
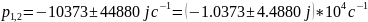
Расчёт добротности:
1.
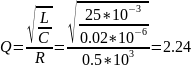
2.
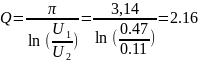
б)
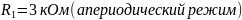 ,
фото 3
,
фото 3
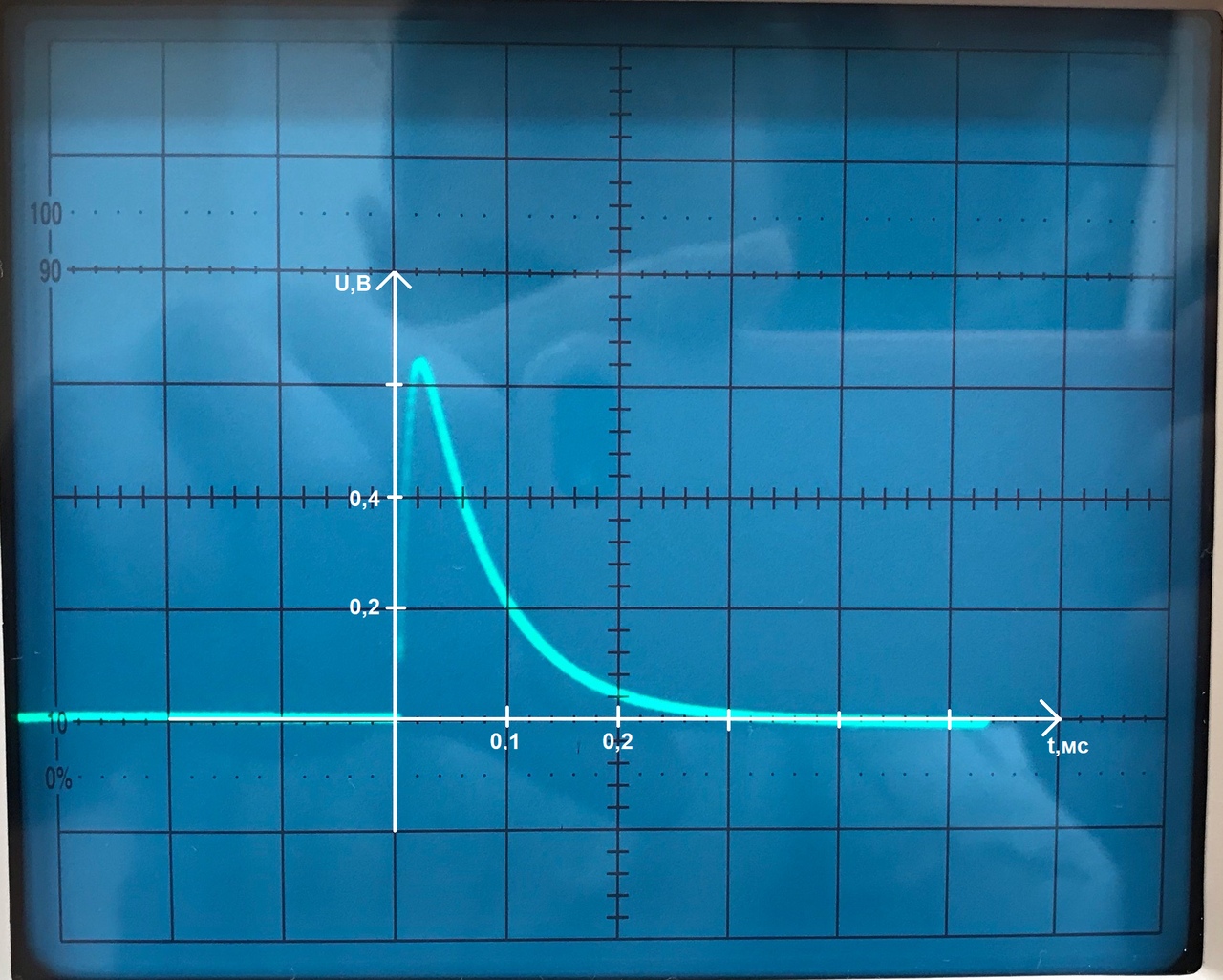
Фото 3.
Теоретический
расчёт:
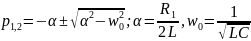
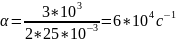
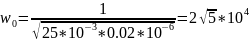
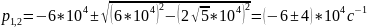
в)
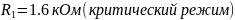 ,
фото 4
,
фото 4
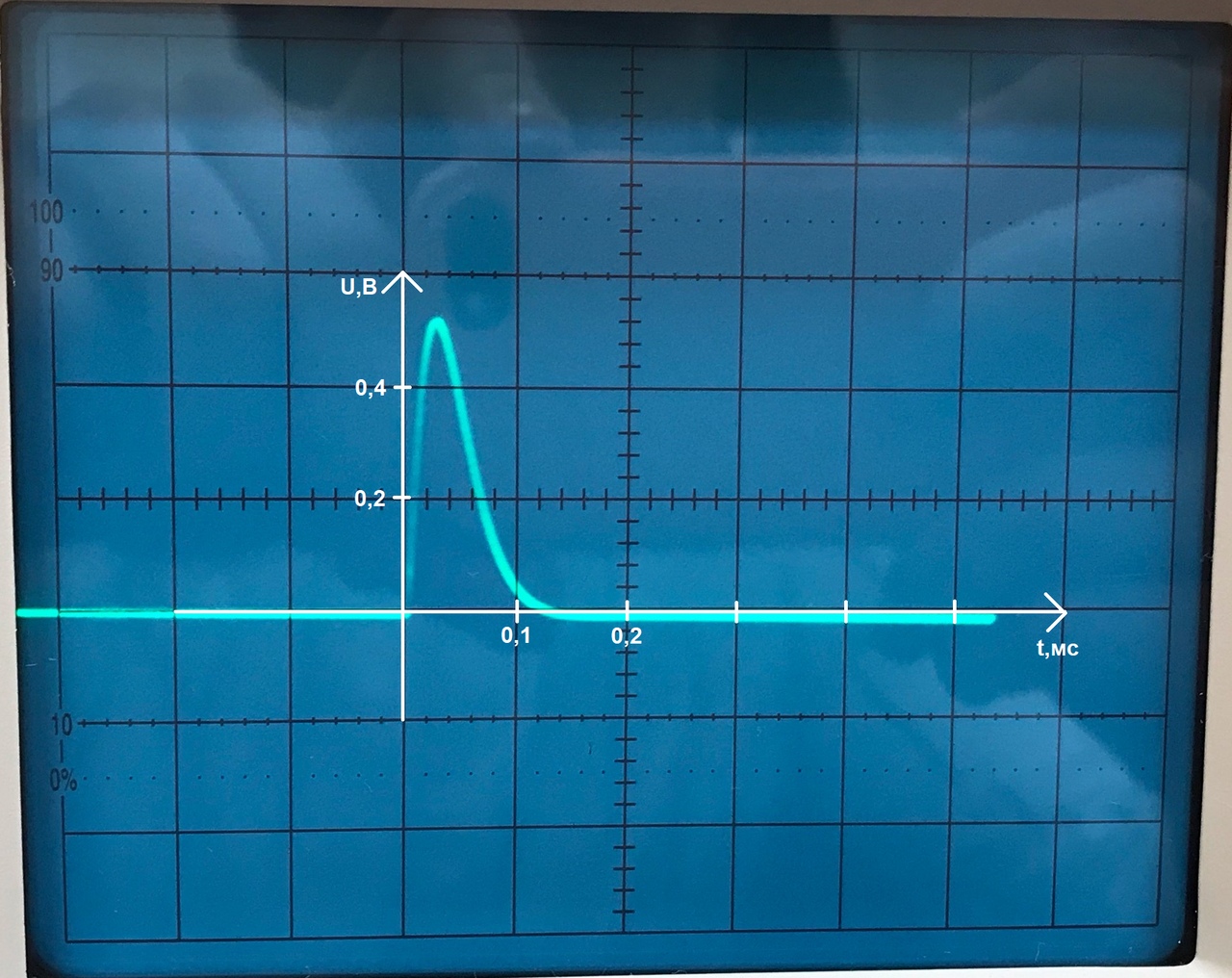 Фото 4.
Фото 4.
Теоретический расчёт:
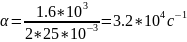
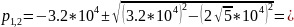
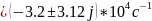 Критический
режим будем при
Критический
режим будем при
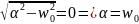
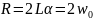 L=
L=
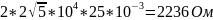
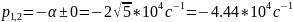
Расчёт по осциллограмме
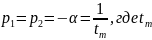 – момент достижения максимума функции
(
– момент достижения максимума функции
(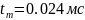 )
)
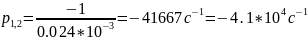
г)
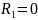 (незатухающий
колебательный режим)
(незатухающий
колебательный режим)
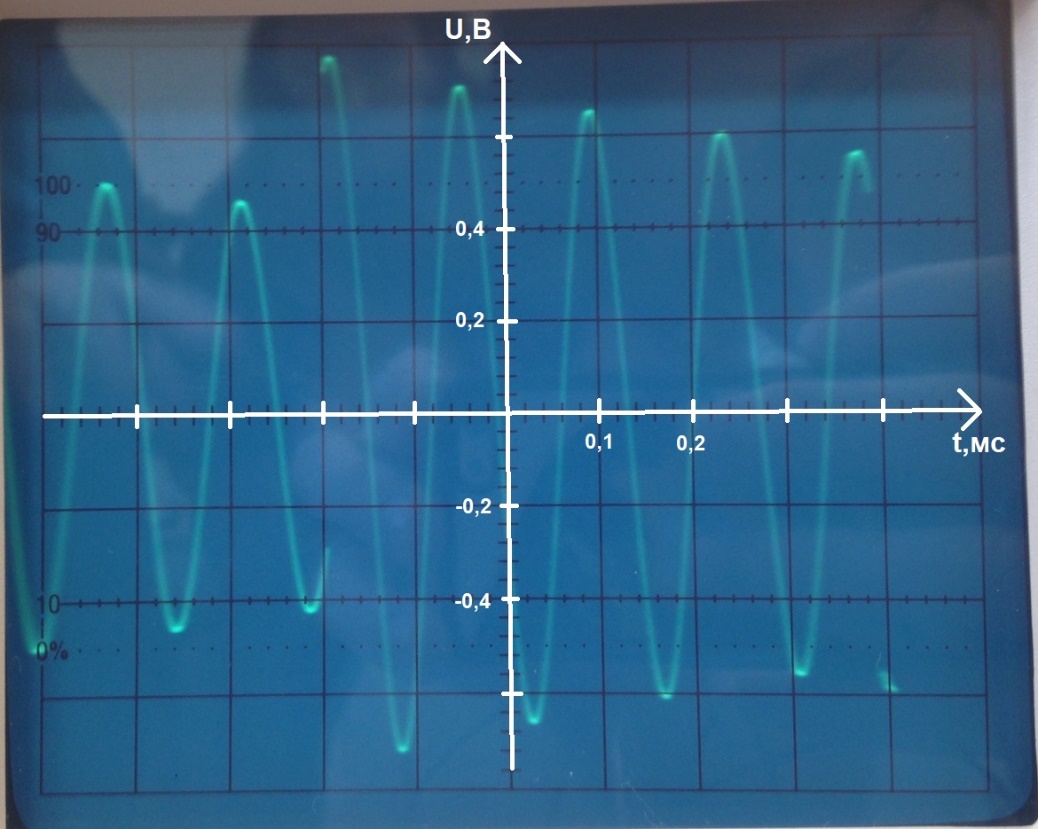 Фото
5.
Фото
5.
Теоретический расчёт:
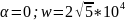
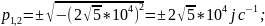
Расчёт по осциллограмме:
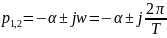
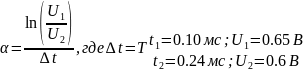

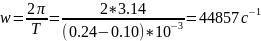
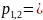 -571.7
-571.7
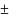 j44857
j44857
Определение добротности контура:
Теоретический расчёт:
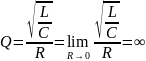
Расчёт по осциллограмме:
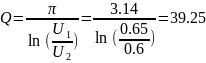
Вопросы:
Какими аналитическими выражениями (в общем виде) описываются процессы во всех четырёх случаях?
Соответствуют ли найденные собственные частоты теоретическому расчёту?
Каковы теоретические значения собственных частот при R1=3 кОм и соответствует ли этим значениям снятая осциллограмма?
Как соотносятся найденные значения добротности с результатами теоретического расчёта?
Ответы:
3.
Колебательный режим:
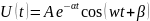 Апериодический режим:
Апериодический режим:
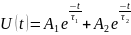 Критический режим:
Критический режим:
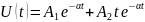 Незатухающий колебательный режим:
Незатухающий колебательный режим:
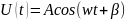
4. Соответствуют ли найденные собственные частоты теоретическому расчету, выполненному согласно (3.2)?
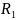 =
0,5 кОм: по осциллограмме:
=
0,5 кОм: по осциллограмме:
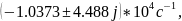
теор.:
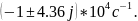
=
1,6 кОм: по осциллограмме:
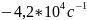
теор.:
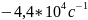
= 0 кОм: по осциллограмме:
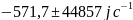
теор.:
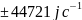
Значения отличаются незначительно. При = 0 кОм существует отличие, т.к. на практике сопротивление существует.
5.
Теоретическое
значение равно:
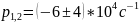 .
Оно примерно соответствует
осциллограмме.
.
Оно примерно соответствует
осциллограмме.
6. При = 0,5 кОм: практ.: Q = 2,16.
теор.: Q = 2,24.
Значения практически совпали.
При = 0 кОм: практ.: Q = 39,25.
теор.:
Q
= .
.
Такое различие связано с тем, что на практике сопротивление существует.
3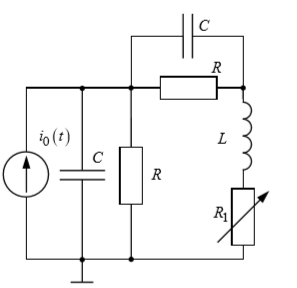 .2.3.
Исследование свободных процессов в
цепи третьего порядка
.2.3.
Исследование свободных процессов в
цепи третьего порядка
С = 0,02 мкФ
R = 5 кОм
= 1 кОм
L = 25 мГн
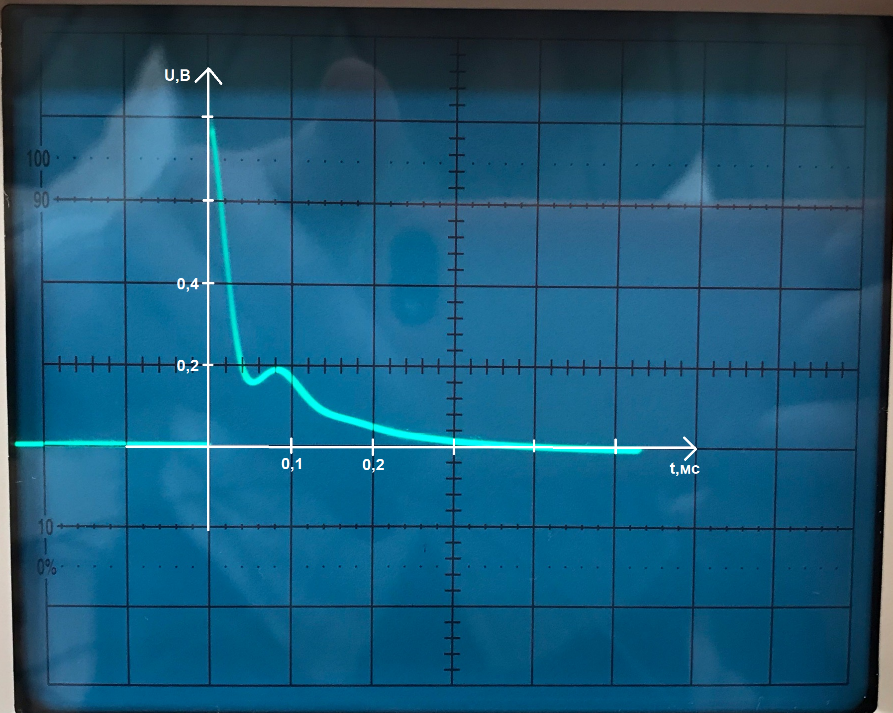
Фото 6.
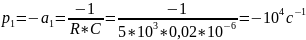

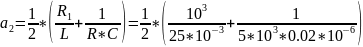
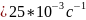

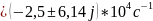
Вопросы:
7. Каким аналитическим выражением описывается осциллографируемый процесс? Соответствуют ли найденные собственные частоты теоретическому расчёту?
8. Каковы значения собственных частот, вычисленные согласно (3.3), и соответствует ли этим значениям снятая осциллограмма?
Ответы:
7.

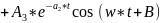
8.
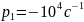
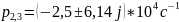
Выводы.
В ходе выполненной работы мы установили соответствие между значениями собственных частот и формой свободного процесса: если собственные частоты вещественные – наблюдается апериодический режим, комплексно-сопряженные – колебательный режим, кратные – критический апериодический режим. Также научились экспериментально определять собственные частоты и добротности RLC-контура по осциллограмме.
