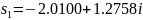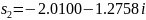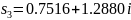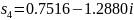Вопрос 2. Как проявляется на временных и частотных характеристиках замкнутой системы наличие неподвижного корня хп?

Ответ:

Частотные характеристики замкнутой системы с неподвижным корнем будут соответствовать характеристикам передаточной функции этой системы с удаленным диполем.

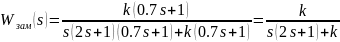
Вопрос 3. Как объяснить характер траекторий подвижных корней хп при изменении ?

Ответ: Для начала рассмотрим ПФ разомкнутой системы:

Луч годографа – направление, в котором двигаются корни замкнутой СУ. Количество лучей определяется разностью количества полюсов и количества нулей. Лучи пересекаются на вещественной оси в точк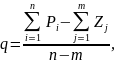е где 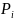- полюса ПФ, 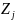- нули ПФ, n – кол-во полюсов 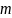– кол-во нулей.

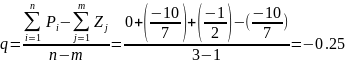
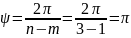– угол между лучами.

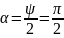– угол от оси к ближайшему лучу.

Вышеприведенные расчеты действительно справедливы для траекторий подвижных корней ХП при изменении 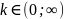, график которых был построен раннее.

Задание 5

1.Текст задания

Для системы из задачи 3 принять ПФ прямой цепи в виде:

.

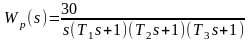Используя изложенную в основных сведениях из теории методику оценки подвижности корней, использующую ЛАЧХ разомкнутой системы 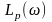, определить диапазон частот (где усиление контура велико), диапазон частот (где усиление контура мало) и приближённые значения отдельных корней ХП замкнутой системы, которые принадлежат этим областям. Найти точные значения корней ХП. Значения постоянных времени , взять из задачи 3, 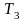определяется вариантом задания.

2. Вариант.

Вариант №13:

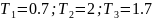
Согласно заданному варианту ПФ будет описана следующими уравнениями:

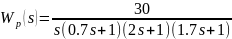
3. Выполнение задания

Используя программные средства MATLAB/Simulink построим график ЛАЧХ для ПФ разомкнутой системы (рис. 18).

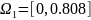На рисунке 18 видно, что частота при которой график ЛАЧХ равняется 20 дБ равна 0.808 . Диапазон частоты . Частота при которой график ЛАЧХ равняется -20 дБ равна 3.25 . Диапазон частоты .

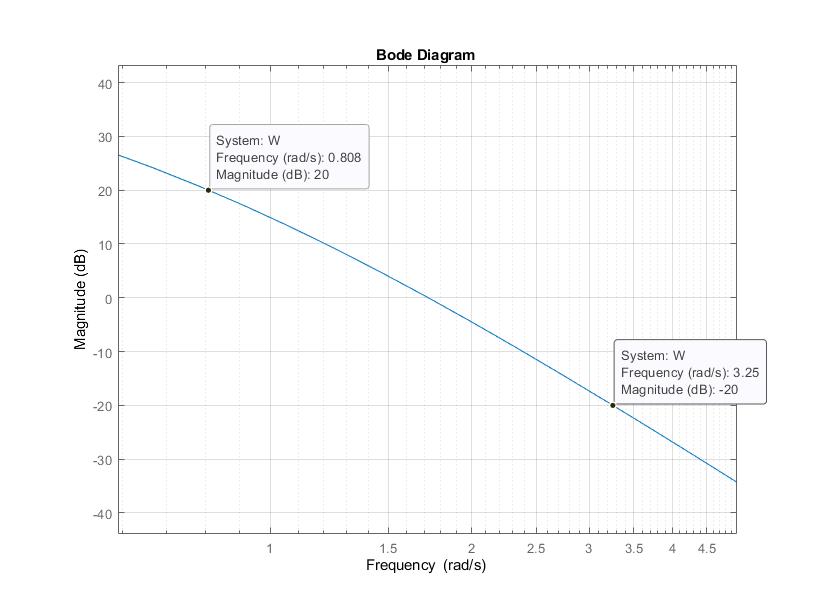
Рис. 18. ЛАЧХ для ПФ разомкнутой системы.

Найдем ПФ замкнутой системы:

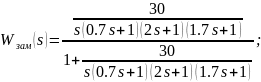
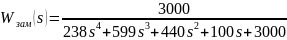
Рассмотрим группы корней ХП замкнутой системы, которые принадлежат областям 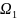и :

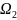• корни, приближённо равные нулям ПФ 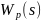разомкнутой системы, модули которых принадлежат области частот, где усиление контура велико, т.е. ;

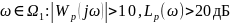В данном случае нули передаточной функции разомкнутой системы отсутствуют.

• корни, приближённо равные полюсам ПФ разомкнутой системы (корням ХП 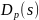), модули которых принадлежат области частот, где усиление контура мало, т. е. .

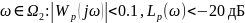То есть на этом частотном диапазоне корни ХП замкнутой системы будут приближенны к полюсам передаточной функции разомкнутой системы, корням 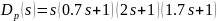, модули которых принадлежат области частот .

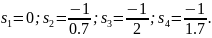
Ни один из модулей этих корней не принадлежат области частот . Поэтому приближенные значения корней замкнутой системы в данном случае определить не удалось.

Используя программные средства MATLAB/Simulink рассчитаем корни характеристического полинома замкнутой системы: