Задание 2
1.Текст задания
Для системы следующего вида
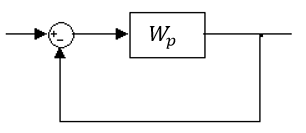
И ПФ
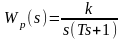
построить
корневой годограф (для замкнутой системы)
при изменении
от нуля до бесконечности. Значение
постоянной времени
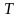определяется вариантом задания.
Для этого следует
последовательно задаваться различными
значениями
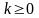и откладывать соответствующие точки,
отвечающие корням, на комплексной
плоскости. Затем точки соединяются
между собой так, чтобы получить непрерывную
линию (траекторию корня). Указать
направление траектории при увеличении
значения
.
Количество точек выбирается таким,
чтобы получить целостное представление
о траектории.
2. Вариант.
Вариант №13:
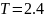
Согласно заданному варианту ПФ будет описана следующими уравнениями:
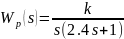
3. Выполнение задания
Найдем передаточную функцию замкнутого контура (замкнутой системы):
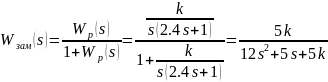
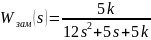
Используя программные средства MATLAB/Simulink был построен корневой годограф для замкнутой системы при изменении от 0 до 100 с шагом 0.01, представленный на рис. 6.
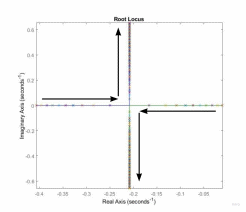
Рис. 6. Корневой
годограф
,
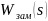где k
изменяется от 0 до 10 с шагом 0.01
4. Ответы на вопросы.
Вопрос 1. Как будут располагаться на комплексной плоскости корни хп при ? Показать траектории.
Ответ:
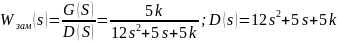
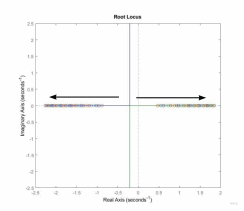
Рис. 7. Корневой
годограф
,
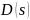где k
изменяется от -1 до -10 с шагом -0.5
Вопрос 2.
Как изменяется переходная характеристика
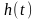замкнутой системы при изменении
коэффициента передачи в интервале
?
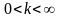Привести качественно различные графики
(т. е. отвечающие различным корням:
простым вещественным; кратным вещественным;
комплексным) и сделать вывод о качественных
изменениях.
Ответ:
Имеем следующую ПФ:
Рассмотрим несколько случаев. 1) простые вещественные корни;
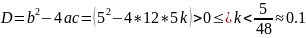
Пусть k = 0.05
2) кратные вещественные корни;
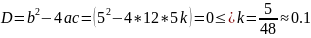
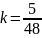
3) кратные комплексные корни;
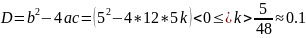
Пусть k = 0.5
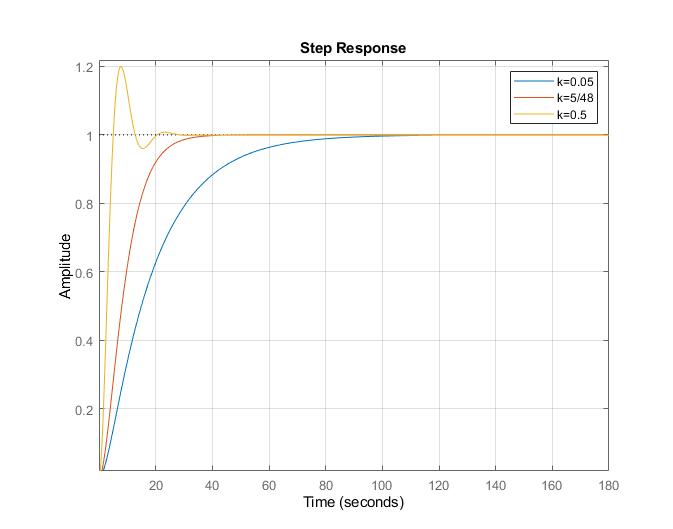Рис.
8. Зависимость переходной характеристики
замкнутой системы при изменении
коэффициента передачи в интервале
.
Иcходя из вышеприведённого графика напрашивается вывод о том, что в зависимости от значения k переходный процесс h(t) может принимать различные формы: при k = 0.05 (простые вещественные корни) и при k = 5/48 (кратные вещественные корни) наблюдаем монотонный сходящийся процесс, а при k = 0.5 (кратные комплексные корни) – колебательный затухающий (сходящийся) процесс.
Задание 3
1.Текст задания
Для той же системы из задания 2 с ПФ вида
,
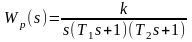построить
корневой годограф при изменении
от нуля до бесконечности. Значения
постоянных времени
и
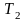определяются вариантом задания.
2. Вариант.
Вариант №13:
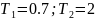
Согласно заданному варианту ПФ будет описана следующими уравнениями:
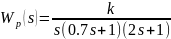
3. Выполнение задания
Найдем передаточную функцию замкнутого контура (замкнутой системы):
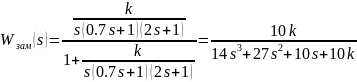
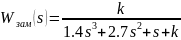
Используя программные средства MATLAB/Simulink был построен корневой годограф для замкнутой системы при изменении от 0 до 100 с шагом 0.01, представленный на рис. 9.
Исходя из того, что в данной системе разность между степенью знаменателя deg D(S) и числителя deg G(S) равняется 3, то корни будут двигаться вдоль асимптот трехлучевой звезды.
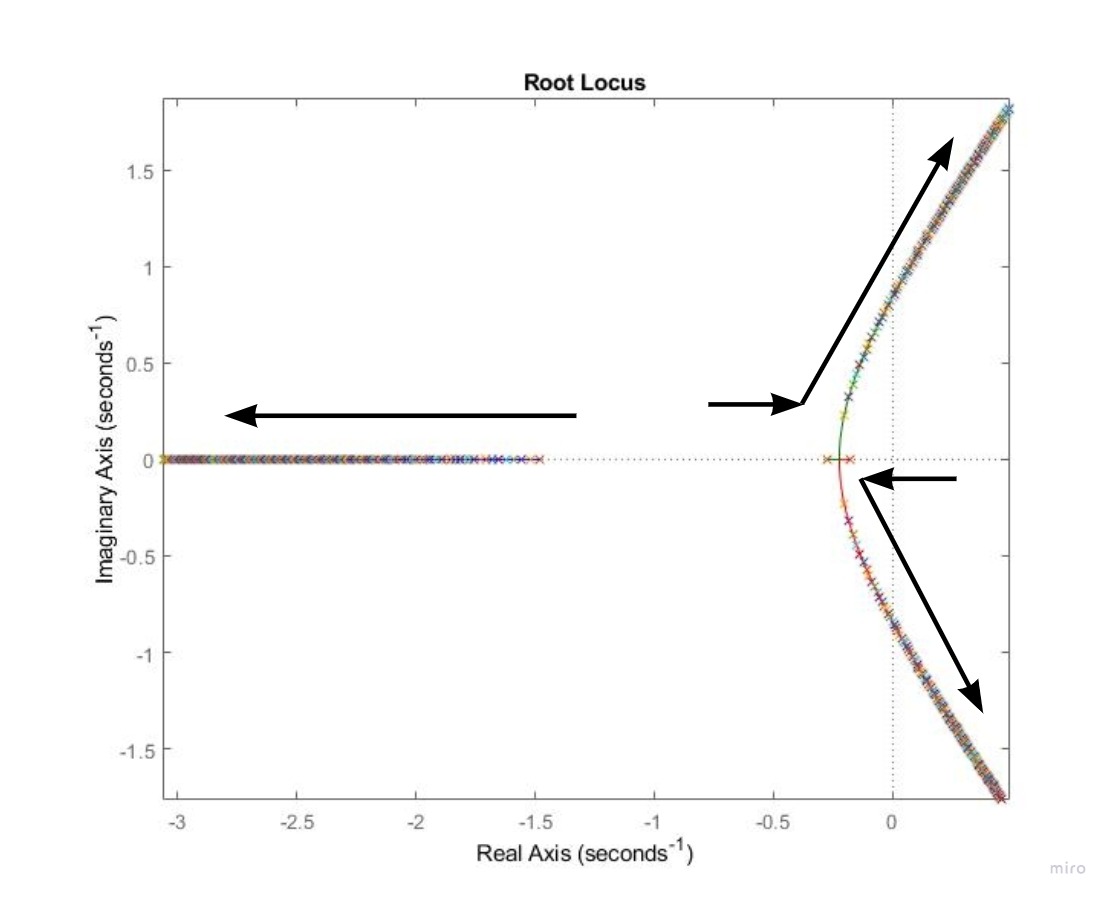Рис.
9. Корневой годограф
,
где k
изменяется от 0 до 100 с шагом 0.01