3.4. Экспериментальное определение оптимального значение коэффициента демпфирования из условия минимума времени затухания процесса.
Исходя из условия
минимума времени
затухания процесса (
время, начиная с которого переходная
характеристика остается в пределах
5% от установившегося значения),
экспериментально был определен
коэффициент демпфирования
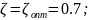
Ниже
на графике (рис. 18) приведены ПХ для ПФ:
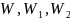у которых коэффициент демпфирования
0.7, 0.69, 0.71 соответственно. Можно заметить,
что именно
является искомой величиной, поскольку
дальнейший рост/уменьшение ζ приводит
к увеличению
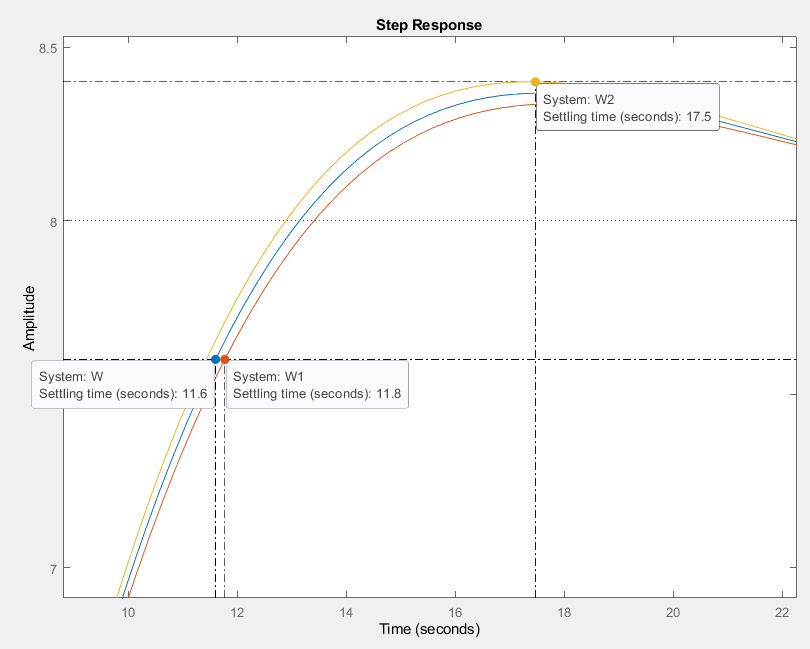
Рис. 18. ПХ для разных
Расположение на комплексной плоскости корней ХП при
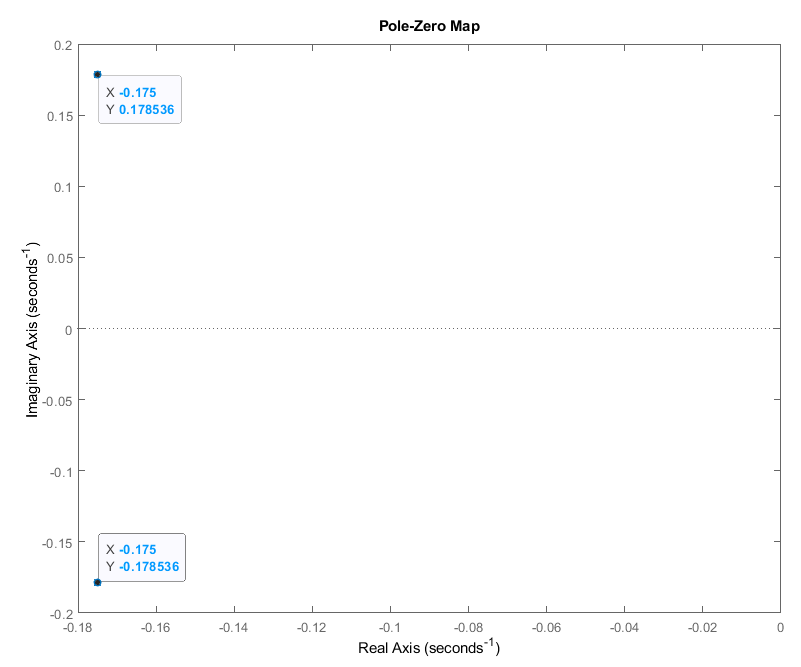
Рис. 19. Расположение корней ХП на комплексной плоскости.
Высота резонансного пика ЛАЧХ и частота резонанса при
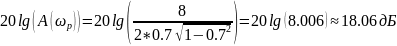
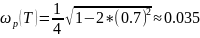
3.5. Переходная и частотные характеристики (афх и лчх) при изменении знака коэффициента демпфирования на .
Найдем характеристики ПФ при отрицательном коэффициенте и сравним с характеристиками ПФ при положительном коэффициенте. Передаточная функция примет следующий вид:
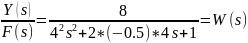
Найдем переходную характеристику:
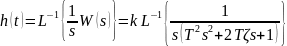
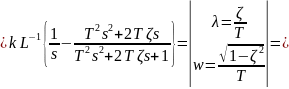
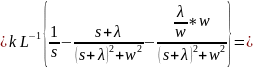
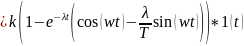
где
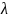– показатель затухания; w
– угловая частота колебаний;
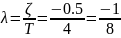
Амплитуда переходной характеристики будет неограниченно расти, так как имеют место положительные комплексно-сопряженные полюсы (рис. 20):
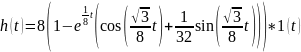
Найдем логарифмические частотные характеристики:
ЛАЧХ не изменится (рис. 21):
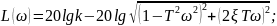
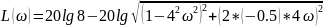
ЛФЧХ зеркально
отразится относительно
(рис. 21):
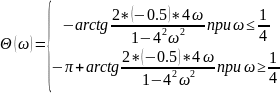
Найдем амплитудно-фазовую характеристику:
АФХ зеркально отразится относительно действительной оси (рис. 22):
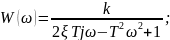
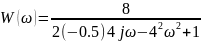
Построим соответствующий график с помощью программного средства MATLAB/Simulink.
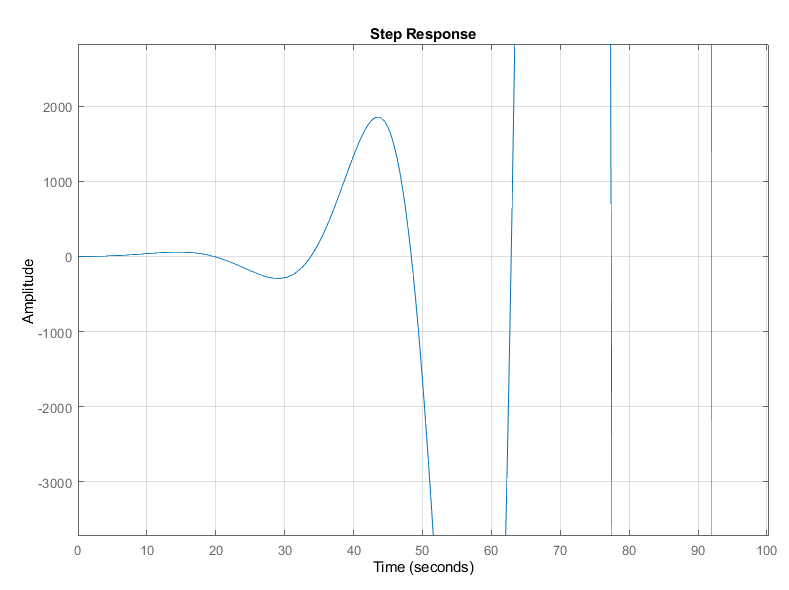
Рис. 20. Переходная
характеристика для
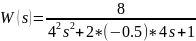
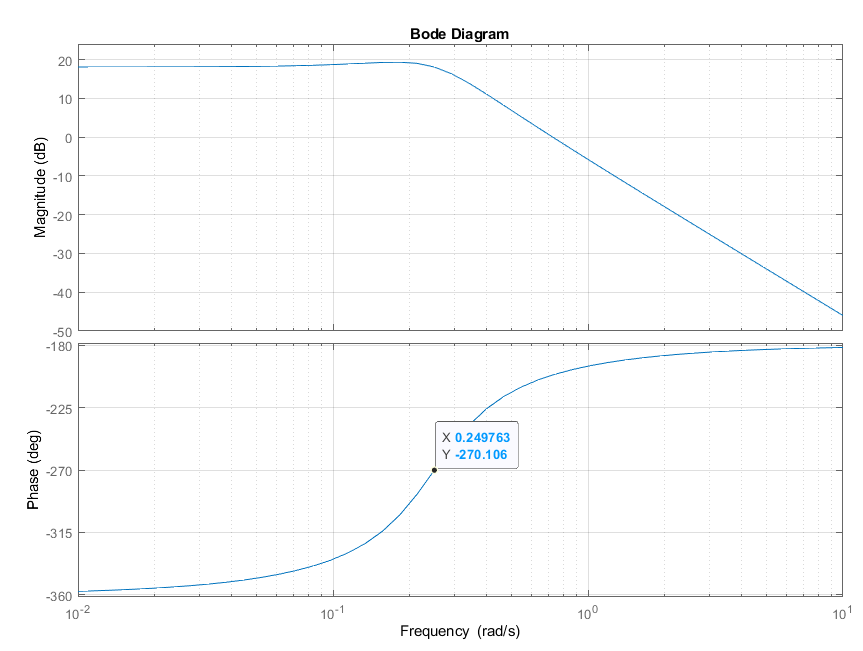
Рис. 21. Логарифмические частотные характеристики для
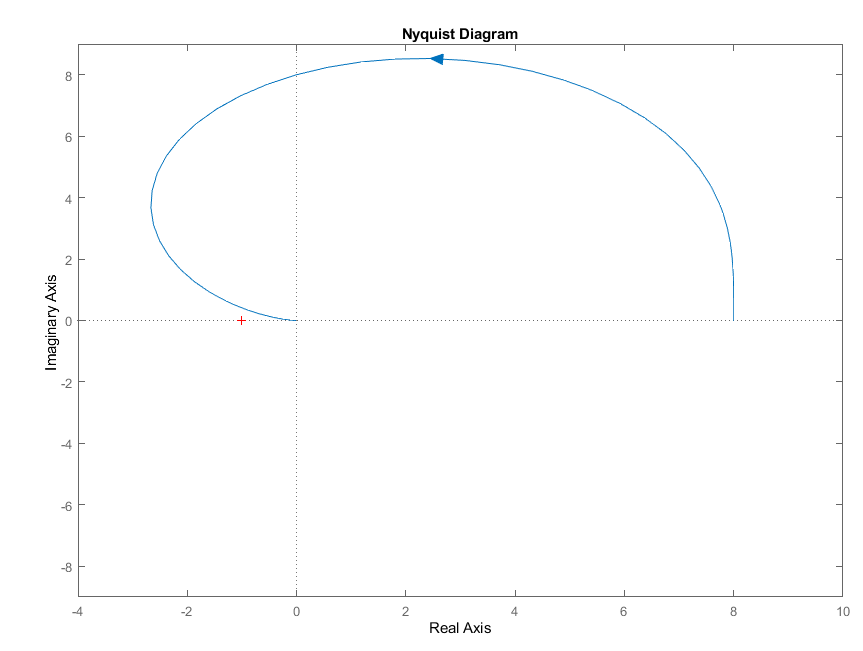
Рис. 22. АФХ для
4. Вывод.
В
результате выполнения задания были
получены ПФ, ПХ, АФХ, ЛАЧХ, ЛФЧХ, а также
изучены свойства апериодического звена
2-го порядка с коэффициентом демпфирования
;
При
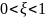звено описывает колебательно-затухающей
переходный процесс.
Было установлено, что движение полюсов при изменении параметра от 0 до 1, начинается с мнимой оси при ξ = 0, и заканчивается отрицательным действительным числом при ξ = 1. Была получена зависимость резонансного пика АЧХ от коэффициента демпфирования, а также приведены советующие графики. Экспериментально было определено оптимальное значение коэффициента демпфирования ξ = ξ опт. = 0.7 из условия минимума времени tр затухания процесса. Были рассмотрены переходная и частотные характеристики при изменении знака коэффициента демпфирования ξ на - ξ: амплитуда переходной характеристики будет неограниченно расти, так как имеют место положительные комплексно-сопряженные полюсы.
Заключение
В
результате выполнения данной лабораторной
работа мы изучили ПХ, ПФ, АФХ, ЛАЧХ и ЛФЧХ
апериодического звена второго порядка,
а также изучили его свойства. Были
разобраны два случаи, когда коэффициент
демпфирования
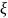= 0 и
= 0,5: при
апериодическое
звено 2-го порядка вырождается в
консервативное
звено,
которое дает незатухающие колебания
на выходе, а при
звено описывается колебательно-затухающим
переходным процессом. Причем уменьшение
повышает колебательность переходных
процессов, кроме того при
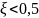ЛАЧХ имеет так называемый «горб» на
сопрягающей частоте, что говорит о
наличии резонанса в системе.
Также
был получен опыт моделирования
передаточных функций и дифференциальных
уравнений в
среде MATLAB/Simulink
и MATLAB
(Command
Window).
Стоит отметить, что параметр
позволяет судить о многих свойствах
системы таких, как колебательность,
резонанс, устойчивость и т.д.
Для передаточной функции, имеющей
коэффициент демпфирования
= 0, частоту резонанса можно было найти
исходя из физических параметров
предоставленной LC-цепи.
Таким образом, знание физических свойств
объекта помогло при исследовании типовых
звеньев.