2. Вариант.
№4 |
|
Определить: |
|
В соответствии с вариантом имеем следующее ДУ:
3. Выполнение задания.
Найдем передаточную функцию:
Для перехода от ДУ к ПФ на первом этапе необходимо воспользоваться оператором дифференцирования:
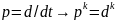
Тогда, применив оператор дифференцирования, уравнение (2) примет следующий вид:
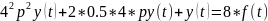
Затем к полученном уравнению применяется прямое преобразование Лапласа, считая, что все начальные условия нулевые:
Тогда по определению передаточная функция примет следующий вид:
Построим график ПХ, АФХ, ЛАЧХ, ЛФЧХ, используя программное средство MATLAB (Command Window):
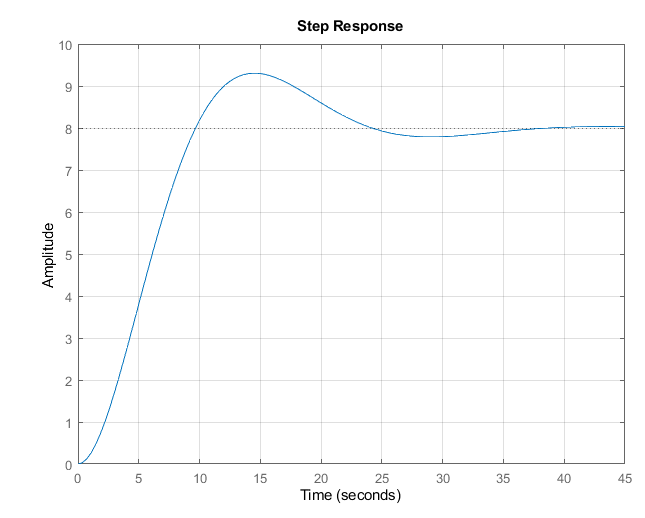
Рис. 12. Переходная
характеристика для
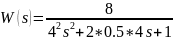
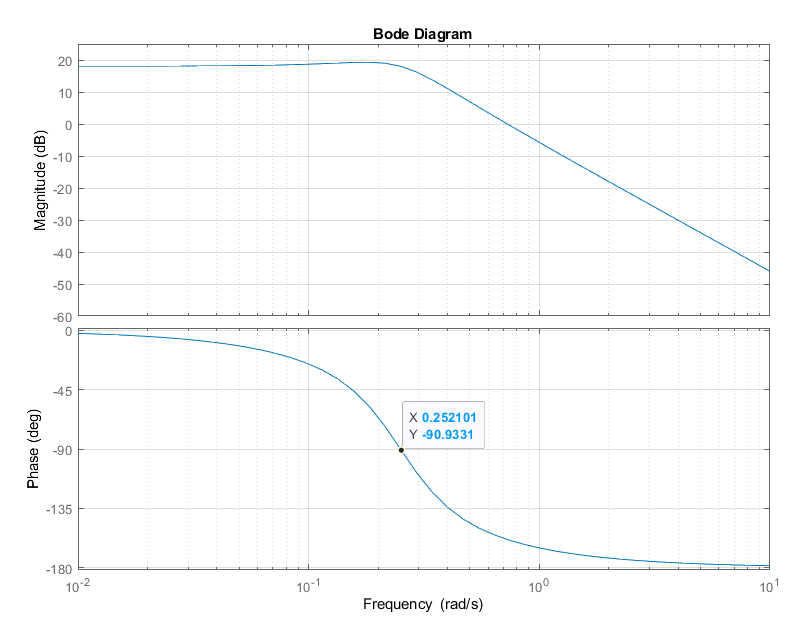
Рис. 13. Логарифмические частотные характеристики для
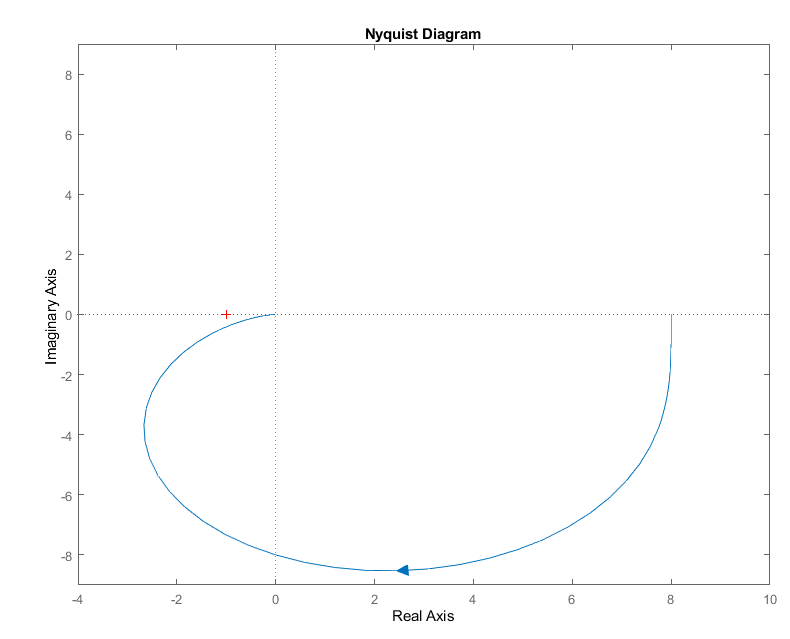
Рис. 14. Амплитудно-фазовая характеристики для
3.1. Проанализируем движение корней (траекторий корней) хп на комплексной плоскости при изменении параметра , приведем графики.
Движение полюсов
при изменении параметра
от 0 до 1, начинается с мнимой оси (полюсы
без действительной части) при
,
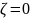заканчиваясь отрицательным действительным
числом при
.
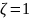Это говорит о том,
что при
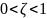звено описывает колебательно-затухающий
переходный процесс. Причем уменьшение
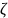повышает колебательность переходных
процессов (так как чем ближе
комплексно-сопряженные полюсы к мнимой
оси, тем больше их мнимая часть и меньше
действительная). Параметр,
определяющий скорость затухания
колебаний в системе, называется
колебательностью.
Колебательность
для пары комплексно-сопряженных корней
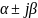вычисляется как отношение мнимой и
вещественной частей корня (по модулю):
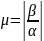Чем больше эта величина, тем слабее
затухают колебания, вызванные этими
корнями, за 1 период колебаний. Колебания
являются затухающими, так как все корни
для этого промежутка
находятся слева от мнимой оси.
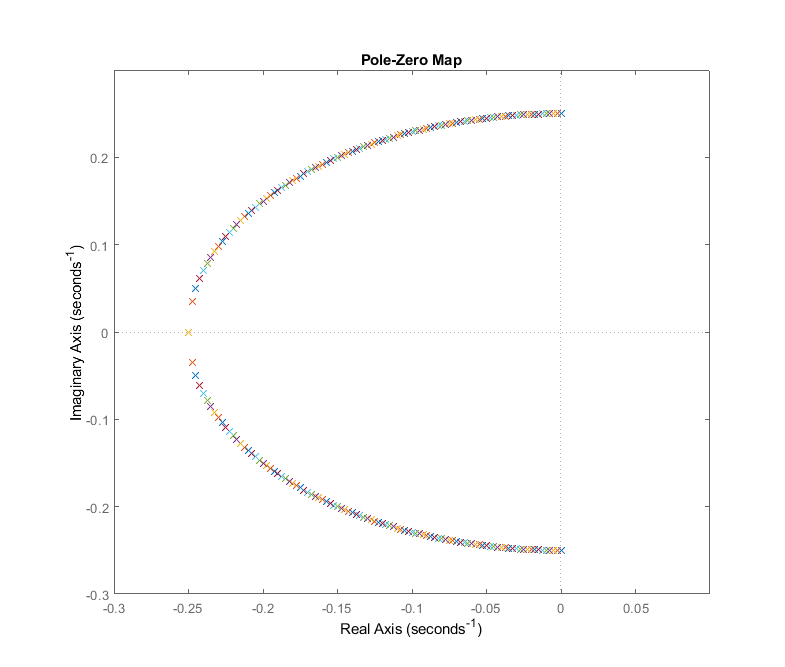
Рис. 15. Движение корней ХП на комплексной плоскости при изменении параметра .
При , звено описывает соединение двух апериодических звеньев 1-го порядка. Переходные процессы имеют монотонно-затухающий вид.
При
Апериодическое
звено 2-го порядка вырождается в
консервативное
звено, которое
дает незатухающие колебания на выходе.
При таком значении ЛАЧХ терпит разрыв
(обращается в бесконечность) на частоте
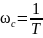, при таком входе амплитуда колебаний
неограниченно растет и на практике
объект разрушается.
3.2. Зависимость резонансного пика ачх от коэффициента демпфирования
Значение пика АЧХ определяется следующей формулой:
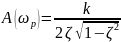
Построим соответствующий график с помощью программного средства MATLAB/Simulink.
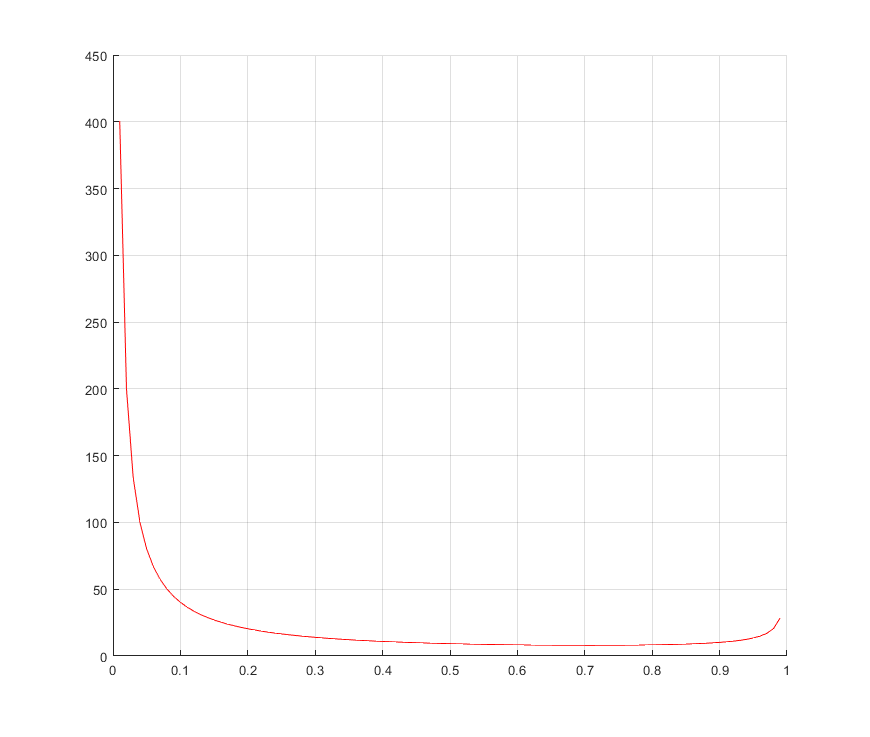
Рис. 16. Зависимость резонансного пика АЧХ от коэффициента демпфирования
3.3. Зависимость резонансной частоты от постоянной времени при выбранном значении .
Примем
=
0.5;
будет определятся следующей формулой:
Построим
соответствующий график с помощью
программного средства MATLAB/Simulink.
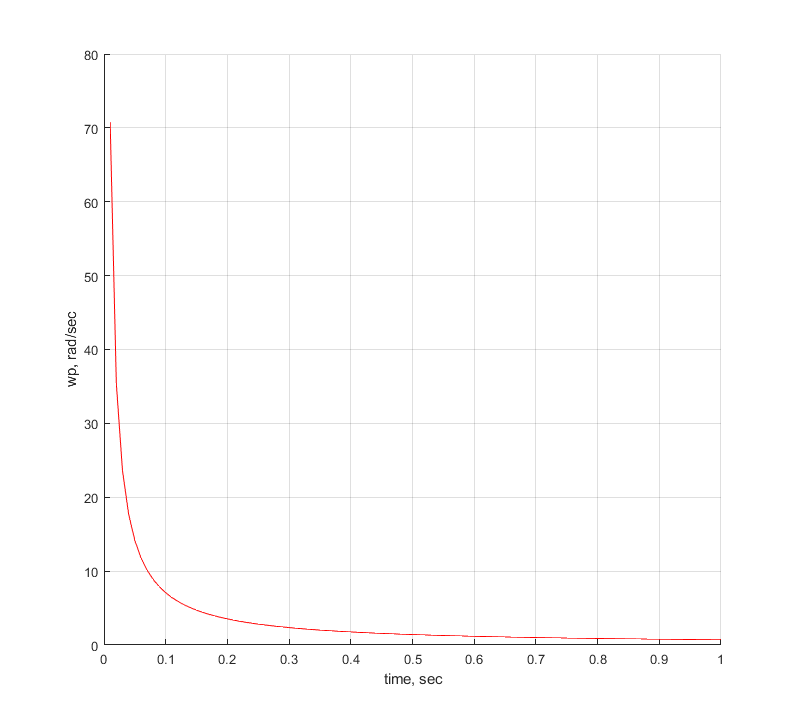
Рис. 17. Зависимость резонансной частоты от постоянной времени при выбранном значении = 0.5 .