ЭД (3.1)

Добавил:

Glavniy_toksik_RTF Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Ульяновский Государственный Технический Университет

Предмет:

Электродинамика

Файл:

мгновенным значениям

∙ sin ∙ cos .

∙ sin ∙ cos .

.pdf

Скачиваний:

Добавлен:

06.08.2022

Размер:

529.03 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

3.1. Поле электрического вибратора

Электрическим вибратором (электрическим излучателем) –

элементарный линейный электрический вибратор – электрический проводник, размеры которого много меньше излучаемой им длины волны, по которому протекает переменный во времени (и постоянный по значению) электрический ток, и поле которого исследуется на расстояниях ℓ. Излучатель подобного типа первым практически реализовал Г. Герц (1887 г), поэтому его часто называют вибратором (диполем) Герца. Электрический диполь с протекающим по нему сторонним током изображены на рисунке.

		̇	̇
Выведем аналитические выражения для напряженности поля и
в любой точке	вокруг излучателя. Ограничимся случаем, когда
ℓ, поэтому		≈ ≈ . Анализ поля удобно проводить	в

сферической системе координат.

Поставленная задача относится к числу тех, в которых целесообразно первоначально определить электродинамический

потенциал ̇поля, а, уже зная его, найти напряженности ̇и ̇. Вычислим векторный (запаздывающий) потенциал поля,

создаваемого электрическим излучателем в точке . Согласно решению волнового уравнения

̇ ( ± )

пр

(, ) =

интегрирование следует выполнять по объему диполя =

ℓ ∙ д

( − )

̇ ∙ e

ст

(, ) =

(ℓд).

неизменна по длине диполя, так

Плотность тока ̇ =

∙ ̇⁄

ст

же величина постоянная из-за удаленности точки .

Тогда

e( − )

(, ) =

∙ ст

∙ ℓ ∙

∙ 0.

Поскольку по определению векторного потенциала ̇

̇= 1 roṫ

и первому уравнению Максвелла для комплексных значений

roṫ= ̇ ̇или ̇= ̇rot ̇,

следовательно, напряженность магнитного поля электрического излучателя определяется вихрем первого порядка векторного

потенциала (roṫ), а напряженность электрического поля – вихрем второго порядка (rot (roṫ)).

Перепишем выражение для векторного потенциала в сферических координатах:

		̇	∙ ℓ		e	( − )
̇		э				( − )
̇		ст
(, ) =				∙				∙ (0 ∙ cos − 0 ∙ sin ),
(, ) =		4		∙				∙ (0 ∙ cos − 0 ∙ sin ),
		4
или			̇ e−
	̇		̇ e−
	(, ) = ∙						∙ (0 ∙ cos − 0 ∙ sin ),
	(, ) = ∙						∙ (0 ∙ cos − 0 ∙ sin ),

где ̇=

∙ ̇ ∙ ℓ ∙ e

ст

Тогда

| ∙

∙

∙ |

rot = ( × ) =

̇∙

̇ ∙

где ,

–

коэффициенты

Ламэ

(для

сферической

системы

координат

= 1, = , = ∙ sin), проекции

равны

e−

= ∙ cos ∙

e−

= ∙ sin ∙

= 0.

Вычисляя определитель,

2 ∙ sin

∙ sin

rot = ( × ) = |

e−

−

∙ cos ∙

∙ sin ∙ e

получаем

̇ ∙ ℓ

( − )

ст

∙ sin ∙ (

+ )

= 0 ∙

Сцелью нахождения аналитического выражения для

напряженности электрического поля ̇нужно определить roṫ. Для этого следует повторить вычисления определителя, заменив в нем

проекции ̇на проекции ̇.

̇	̇	̇
Из полученного выражения для очевидно,	что	= = 0.

Тогда

			0			0
	\| 2 ∙ sin				∙ sin
̇
̇
rot =
	\|
	\|
		0		0

стэ̇ ∙ ℓ

	0
			\|
			,


			e( − )\|
1			e( − )\|
∙ sin ∙ (		+ )
∙ sin ∙ (		+ )

Результатом вычислений является выражение

	э			1			1					e	( − )
̇	̇ℓ			1			1			2		e
̇	ст									2
=		{	[2cos (		+	)] + [sin (		+	−		)]}			.
=	4	{	[2cos (	2	+	)] + [sin (	2	+	−		)]}			.
	4	0		2		0	2

Полученные выражения позволяют рассчитать напряженность электромагнитного поля всюду (при ℓ) вокруг электрического излучателя. Анализируя полученные выражения, легко заметить, что

как ̇, так и ̇содержат слагаемые, по-разному зависящие от . Поэтому в зависимости от удаленности точки от электрического излучателя

определяющий вклад в величины ̇ и ̇ будут вносить разные слагаемые. В связи с этим принято выделять ближнюю зону ( 1),

промежуточную зону ( ≈ 1) и дальнюю зоны ( 1) поля излучателя, где = 2⁄ .

Поле электрического вибратора в ближней зоне

Ближней называется зона, в которой расстояние от точки наблюдения до электрического мало по сравнению с длиной излучаемой волны ( ℓ, но , т.е. ℓ ). Поэтому в фазовой

части выражений для ̇и ̇члены = 2⁄ 1 и , что позволяет пренебречь ими. Аналогично, выделяя в амплитудной части

наиболее сильные слагаемые, получаем:

∙ ℓ

ст

≈

∙

∙ sin ∙ e

4 2

̇ℓ

ст

≈

[ 2cos + sin ]e

∙ ̇ℓ

= −

ст

[ 2cos + sin ]e

= ( ̇

+ ̇

)e( − ⁄2).

Рассмотрим магнитное поле в ближней зоне. Переходя к

Сравним записанное выражение с напряженностью магнитного поля , создаваемого элементом длины ℓ постоянного линейного тока , определяемого законом Био–Саввара:

= 0 ∙ 4 ∙ ℓ2 ∙ sinθ.

Так как при выводе формул для поля, создаваемого элементарным электрическим излучателем, предполагалось, что ток излучателя равенстэ = стэ ∙ cos, то напряженность магнитного поля излучателя в ближней зоне совпадает с напряженностью магнитного ноля, вычисленной на основе закона Био–Савара, при усложни, что постоянный ток (равен току излучателя в рассматриваемый момент времени.

Перейдем к анализу электрического поля излучателя в ближней эоне. Изменение тока в излучателе приводит к изменению величины зарядов на его концах (суммарный заряд излучателя в любой момент времени равен нулю, а заряды на его концах равны по величине и противоположны по знаку). При этом для каждого из концов излучателя выполняется закон сохранения заряда = − ⁄ . Следовательно, заряды изменяются по закону = ± sin, где = ⁄ . Знак « + » соответствует верхнему концу излучателя ( = +ℓ/2), а знак «–» – нижнему ( = −ℓ/2). Переходя к мгновенным значениям составляющих

	на получаем
вектора , заменив	на получаем

					ℓ
		=							cos ∙ sin,
		=	2				3		cos ∙ sin,
			2				3

						ℓ
		=							sin ∙ sin .
		=		4				3	sin ∙ sin .
				4				3

Таким образом, в ближней зоне элементарный электрический излучатель создает такое же электрическое поле, как и электростатический диполь с моментом = 0ℓ, заряды которого равны зарядам, сосредоточенным на концах излучателя, в рассматриваемый момент времени.

Как видно из общих выражений для ̇ и ̇ составляющие напряженности электрического и магнитного полей в ближней зоне

сдвинуты по фазе, а именно ̇	и	̇	сдвинуты по фазе на 90°

относительно Ḣφ.

Это не означает, конечно, что в ближней зоне отсутствует излучение. В выражениях для поля имеются слагаемые, пропорциональные 1⁄ , которые определяют излучаемую энергию. Однако их абсолютные величины малы по сравнению с абсолютными величинами составляющих , и . Это означает, что в ближней зоне имеется относительно большое реактивное поле. Полный поток энергии во всех зонах одинаков (предполагается, что в среде отсутствуют потери).

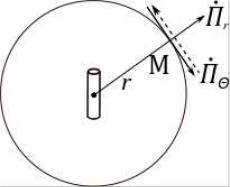
Комплексный вектор Пойнтинга оказывается чисто мнимой величиной, а его среднее значение – равным нулю. Потоки мощности

поля, ориентированные в направлениях	и	(П̇ =	1		и П̇	=
			2	̇ ∙ ̇
0	0

1̇∙ ̇), носят реактивный (колебательный) характер (рисунок).

Сформулированные выводы приближенны, так как они связаны с учетом неравенства . Фактически сквозь ближнюю зону проходят волны, несущие с собой радиально направленный поток активной мощности, подведенной от источника к диполю. Этот поток проходит затем через промежуточную и дальнюю зоны, формируя поле излучения диполя. Однако в ближней зоне поток активной мощности пренебрежимо мал по сравнению с большим реактивным потоком.

Поле электрического вибратора в дальней зоне

В дальней зоне (естественно, ℓ). Поэтому величиной в показателе экспоненты пренебрегать нельзя, а в амплитудной части

общих выражений

наиболее

весомыми

будут члены,

для

содержащие −1

∙ ℓ

( − )

ст

∙ sin ∙ (

+ )

= 0 ∙

( − )

̇ℓ

ст

{ [2cos (

)] + [sin (

−

)]}

наиболее весомыми будут члены, содержащие −1

( − )

̇ ∙ ℓ ∙

( −+⁄2)

ст

∙

∙ sin

∙

( − )

̇ℓ

ст

[

∙

∙ cos −

∙

∙ sin ]

( − )

( −+⁄2)

= ∙ e

+ e

В дальней зоне поле по-прежнему имеет три составляющие ( ̇, ̇,

̇),

однако

его

характер

качественно

изменился

по

сравнению

ближней зоной. Составляющие поля распространяются от центра диполя в виде сферических волн (содержат сферическую функцию

Грина ).	Составляющие ̇,	̇	колеблются	в	фазе,	поэтому

создаваемый	ими радиальный	поток	мощности	поля	П̇ =	1
создаваемый	ими радиальный	поток	мощности	поля	П̇ =	2	̇ ∙ ̇
						2

имеет чисто реальный характер. Эта мощность, уходящая от диполя, –

мощность излучения. Составляющие ̇,	̇	колеблются с фазовым

сдвигом 90°, что приводит к реактивному характеру создаваемого ими

потока мощности П̇	=	1		. Поток	скользит вдоль , меняя на
		2	̇∙ ̇
					0
180° свое направление			через	каждые	полпериода колебаний поля

(рисунок).

Поскольку |П̇|~ −3, а |П̇|~ −2, в дальней зоне реактивный поток мал по сравнению с активным и с удалением от диполя неравенство

закону −2, последней составляющей можно пренебречь и приближенно описывать поле выражениями

( − )

∙

̇ ∙ ℓ ∙

ст

∙ sin ∙

( − )

∙ ̇ ∙ ℓ ∙

ст

sin ∙

что = 2 ⁄ = ⁄ ,

= 1⁄

Учитывая,

√

и, соответственно,

2 = 2

⁄ , получим

√

∙ ℓ ∙

ℓ

ст

∙ sin =

ст

∙ sin ,

ℓ

ст

sin .

√

Можно найти среднюю плотность потока мощности П = ReП,

получим в дальней зоне электрического

учитывая, что П̇=

( ̇× ̇),

излучателя

ℓ

ст

П = 0

(

)

√

sin

На рисунке представлена картина силовых линий поля электрического диполя.

В дальней зоне электромагнитное поле элементарного электрического излучалетя представляет собой сферическую волну, распространяющуюся со скоростью, равной скорости света в данной среде.

Поле электрического вибратора в дальней зоне

Функция, описывающая зависимость величины составляющих поля от угловых координат , , называется функцией направленности. Графическое изображение этой функции на плоскости или в трехмерном пространстве принято называть диаграммой

направленности. Пренебрегая в дальней зоне малой составляющей ̇,

видим, что направленные свойства излучения электрического диполя описываются функцией

( ) = sin

которая в любой плоскости сечения, проходящей через ось диполя, изображается «восьмеркой». Так как ( ) не зависит от , что является естественным ледствием осевой симметрии излучателя-диполя, то объемное изображение ( ) в сферических координатах имеет вид тора.

Наиболее интенсивно электрический диполь излучает в экваториальной плоскости ( = 90°). Если напряженность поля илив некоторой точке этой плоскости принять за единицу, то при движении по дуге постоянного радиуса в меридиональной плоскости напряженность поля будет уменьшаться по закону синуса. Вдоль своей оси ( = 0° и 180°) диполь не излучает.

Мощность излучения электрического вибратора

Распространение волны сопровождается переносом энергии.

Средняя за период плотность потока мощности равна П = ReП̇, в

которую следует подставить комплексный вектор П̇= 12 (̇× ̇) для

поля электрического излучателя. Комплексный вектор Пойнтинга в рассматриваемом случае является чисто вещественной величиной.

Средняя мощность, излучаемая в пространство электрическим излучателем, находящимся в среде без потерь, равна среднему потоку мощности через любую замкнутую поверхность, окружающую излучатель

изл = П .

Вычисление интеграла упрощается, если в качестве поверхности , охватывающей излучатель, используется сфера с центром в начале координат и достаточно большим радиусом , чтобы выполнялось условие 1 (дальняя зона).

В сферической системе координат элемент поверхности

= 0 ∙ 2sin ∙ .

Учитывая, что в дальней зоне

э ℓ

= ст2 ∙ sin,

э ℓ

= ст √ sin, 2

проходящая через элементарную площадку dS сферы средняя мощность будет равна

1 / 21 2 > Следующая >>>

Соседние файлы в папке Электродинамика .pdf

#
06.08.2022540.87 Кб9ЭД (2.4).pdf
#
06.08.2022259.86 Кб9ЭД (2.5).pdf
#
06.08.2022259.25 Кб9ЭД (2.6).pdf
#
06.08.2022391.87 Кб9ЭД (2.7).pdf
#
06.08.2022409.5 Кб9ЭД (2.8).pdf
#
06.08.2022529.03 Кб10ЭД (3.1).pdf
#
06.08.2022347.47 Кб10ЭД (3.2).pdf
#
06.08.2022358.77 Кб10ЭД (3.3).pdf
#
06.08.2022315.12 Кб10ЭД (4.1).pdf
#
06.08.2022456.78 Кб9ЭД (4.3).pdf
#
06.08.2022363.6 Кб11ЭД (4.4).pdf