Электродинамика (РТФ, Климовский, 5 семестр) / Электродинамика .pdf / ЭД (5.5)

5.5.Взаимодействие волны с поверхностью хорошо проводящей среды

Среда с хорошей проводимостью ( 2 – велико) характеризуется

реально встречаемых видов почв при решении задач распространения радиоволн над поверхностью Земли.

Вспомним второй закон Снелля 1 ∙ sinΘотр = 2 ∙ sinΘпр. На основании его можно сделать два важных вывода. Во-первых, большое

значение |̇| хорошо проводящей среды приводит к тому, что угол

2

Θпр → 0: вглубь среды с большой проводимостью наклонно падающие на ее поверхность волны уходят почти по направлению внутренней

нормали. Во-вторых, комплексный характер ̇ требует (для

2

соблюдения равенства второго закона Снелля), чтобы sinΘпр и, следовательно, угол Θпр приняли комплексное значение. Это следует понимать так, что в преломленной волне фронты фаз и амплитуд перестают пространственно совпадать друг с другом (рисунок).

Такую волну называют неоднородной. Зависимость преломленной волны от координат описывается выражением

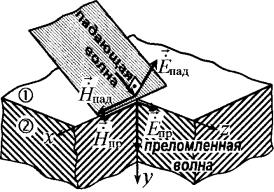
непараллельными. Фронт фаз наклонен к поверхности раздела сред и движется в направлении, обозначенном на рисунке штриховой линией. Угол tg = 2 ⁄ 2′ имеет смысл угла преломления.

Тот факт, что преломленная волна движется вглубь хорошо проводящей среды почти по нормали к пограничной поверхности (рисунок) и по своей структуре близка к плоской волне, позволяет ввести приближенные граничные условия (они называются условиями Леонтовича), удобные для расчета поля в 1-й среде у поверхности раздела.

Во 2-й среде (например, при вертикально-поляризованной

Таким образом, у поверхности хорошо проводящей среды отношение касательных составляющих электрического и магнитного полей 1-й среды определяется параметрами 2-й среды.

Свойство среды с большой проводимостью как бы втягивать распространяющуюся над её поверхностью волну и поглощать мощность последней имеет важное практическое значение. Приведем два примера из практики.

На рисунке показано, как при скольжении падающей волны по поверхности хорошо проводящей среды за счет оттока энергии волны

во 2-ю среду фронт волны и вектор ̇пад по мере движения в направлении оси постепенно наклоняются к границе раздела, вектор

П̇пад все круче «зарывается» во 2-ю среду. Если волна с наклоненным фронтом падает на Г-образную антенну приемника, то токи, возбуждаемые в вертикальном и горизонтальном плечах антенны, текут в одном направлении (сплошные стрелки на рисунке) – волна принимается.

При движении волны в противоположном направлении указанные токи будут протекать навстречу друг другу (штриховые стрелки на рисунке) – прием волны ослаблен. Таким образом, явление наклона фронта волны при ее движении над хорошо проводящей средой приводит к возникновению невзаимности приема волны, хотя среды 1-я и 2-я изотропны.

Допустим, что рассматриваемая волна излучается антенной, имеющей диаграмму направленности, показанную сплошной кривой (рисунок).

Если бы 2-я среда была лишена потерь, форма диаграммы направленности (на каком бы расстоянии от антенны она ни измерялась) осталась бы неизменной. Большие потери во 2-й среде приводят к тому, что на значительном удалении от антенны в диаграмме направленности возникает завал, возрастающий по мере удаления от антенны (см. штриховые линии на рисунке). В результате максимум чувствительности антенны отклоняется от горизонтального направления на угол . Это может вызвать трудности радиолокации низколетящих целей.