Электродинамика (РТФ, Климовский, 5 семестр) / Электродинамика .pdf / ЭД (4.3)

4.3. Электромагнитные волны в анизотропной плазме

Плазма – частично или полностью ионизированный газ, образованный из нейтральных атомов (или молекул) и заряженных частиц (ионов и электронов), будучи помещенной в магнитное поле, становится анизотропной средой. С намагниченной плазмой приходится иметь дело при решении задач распространения радиоволн в ионосфере Земли, которая располагается на высоте 60…20 000 км. В различных приборах приходится иметь дело с плазмой газового разряда, а также плазмой, образуемой носителями заряда в металлах и полупроводниках.

При конечной температуре плазмы входящие в ее состав частицы всех трех сортов находятся в непрерывном движении, обмениваясь взаимными ударами. Полная хаотичность теплового движения приводит к совершенно симметричному распределению скоростей частиц по направлениям. Такая плазма изотропна, и радиоволны в ней в любом направлении распространяются одинаково.

Относительная диэлектрическая проницаемость изотропной плазмы

самопроизвольно в результате случайного пространственного разделения в плазме электронов и ионов и появления в связи с этим электростатических сил взаимного притягивания, приводящих электроны в колебательное движение (ленгмюровские колебания);

– частота упругих столкновений в плазме электронов и нейтральных частиц (атомов и молекул), она определяет потери энергии электромагнитной волны, – круговая частота электромагнитной волны, распространение которой мы рассматриваем. Для плазмы земной

ионосферы ~1012 м−3, для плазмы проводящих твердых тел

~1026 м−3.

Появление постоянного магнитного поля 0 качественно изменяет свойства плазмы. Электроны и ионы, вектор скорости которых ориен-

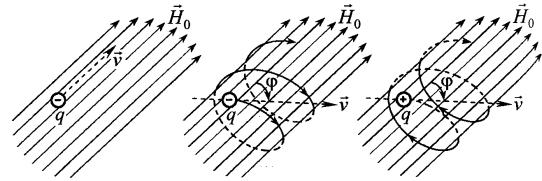
тирован к силовым линиям поля 0 под углом , отличным от нуля, испытывают действие силы Лоренца

л = ∙ 0 ∙ ( × 0)

и начинают двигаться по круговой цилиндрической спирали, «навитой» вокруг линий магнитного поля под тем же углом и имеющей радиус

зависит от знака заряда частицы (рисунок)

Таким образом, постоянное магнитное поле, наводя определенный порядок в движении заряженных частиц плазмы, создает асимметрию пространственного распределения их скоростей. Теперь уже электромагнитные волны в разных направлениях (например, вдоль или поперек 0) распространяются по-разному. Плазма становится анизотропной. В уравнениях Максвелла это новое свойство намагниченной плазмы отражается введением тензора относительной диэлектрической проницаемости

Здесь введено обозначение – циклотронная частота – частота вращения заряженной частицы вокруг силовых линий 0 при движении по спиральной траектории

ц = 0 0.

Анализ выражений для тензора диэлектрической проницаемости дает возможность выявить важные особенности взаимодействия электромагнитных волн с намагниченной плазмой. В частности, при отсутствии потерь, т.е. при отсутствии столкновений ( = 0), или когда частотой столкновений можно пренебречь ( ), плазма называется бесстолкновительной, компоненты тензора диэлектрической проницаемости и бесконечно возрастают, когда = ц. Это свидетельствует о развитии в плазме резонансного процесса. В

намагниченной плазме резонансным образом увеличивается радиус спиральной траектории движения заряженных частиц

(циклотронный резонанс).

Вплазме легко достигается также ситуация, когда диагональные компоненты тензора принимают нулевое значение. Это явление известно как плазменный резонанс, суть которого заключается в раскачке электромагнитной волной ленгмюровских колебаний в плазме.

Вдиапазоне частот, где < пл, диэлектрическая проницаемость плазмы становится отрицательной: волны в такой среде распространяться не могут (явление отсечки).

Компоненты тензора , а следовательно, и связанные с ними показатель преломления плазмы, фазовая скорость волны зависят от её частоты. Поэтому в плазме наблюдается заметная дисперсия волн.

Перечисленные явления не исчерпывают всех особенностей плазмы, однако и они уже свидетельствуют о большом разнообразии эффектов, сопровождающих процесс взаимодействия электромагнитных волн с этой средой.

Рассмотрим подробнее распространение электромагнитных волн в намагниченной плазме. Пусть постоянное во времени однородное

магнитное поле 0, ориентированное под углом Θ к оси , пронизывает пространство, заполненное бесстолкновительной плазмой (учет потерь серьезно загромоздил бы математические выкладки, лишив их наглядности). Если плоская электромагнитная волна бежит в

подобных условиях вдоль оси , то, как показывает подробный анализ уравнений Максвелла, показатель преломления плазмы описывается выражением

где ц = ц ∙ sinΘ, ц = ц ∙ cosΘ – соответственно «поперечная» и «продольная» циклотронные частоты. Амплитуды поперечных и составляющих электрической компоненты волны определяются соотношением

Связь продольной составляющей электрической компоненты с поперечными имеет вид

Рассмотрим частные случаи.

Распространение плоской волны в плазме вдоль поля намагничивания

При продольном распространении (Θ = 0) векторы 0 и П бегущей волны ориентированы параллельно оси . Поэтому

ц = 0, ц = ц и

Знаки «±» означают, что уравнения Максвелла для сформулированной задачи имеют два решения, т.е. первоначальная плоская линейнополяризованная волна «распадается» на две волны, бегущие в общем-направлении с постоянными распространения

возникающих при продольном распространении плоской волны в намагниченной плазме, поляризованы по кругу в противоположных направлениях. Описанное явление называется эффектом Фарадея (продольным магнитооптический эффектом Фарадея),

который заключается в том, что при распространении линейно-

Рассмотрим ситуацию, иллюстрирующую необходимость учета эффекта Фарадея на практике. Предположим, что два космических аппарата, вращающихся вокруг Земли на высоте 300 км, снабжены антеннами в виде симметричных вибраторов. Пусть антенны параллельны друг другу. Между аппаратами ведется обмен информацией на частоте 30 МГц, причем радиоволны распространяются в направлении, параллельном силовым линиям магнитного поля Земли. При взаимном удалении аппаратов, если на трассе, разделяющей

космические аппараты, плоскость поляризации вектора ̇радиоволны повернется на 90°, в результате действия эффекта Фарадея связь между ними прервётся.

(показатель преломления становится мнимой величиной) и отражения волны от границы области, на которой пл = 0 и пл = 0.

Тогда условие отсечки

выполняется при

На рисунке показано изменение относительной диэлектрической проницаемости плазмы (или, что то же самое, пл2 ) в зависимости от квадрата соотношения частот волны и плазменных колебаний. Рисунок

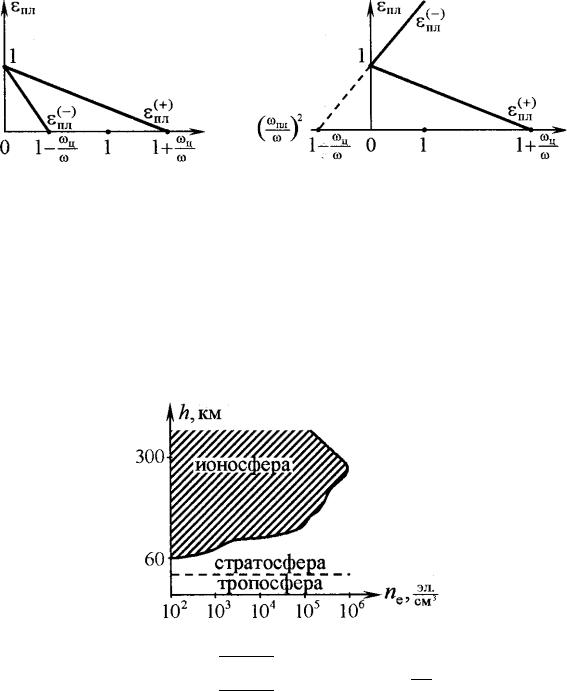
слева справедлив для волн с частотами, превышающими циклотронную частоту ц; рисунок справа – для ситуации < ц.

Воспользуемся полученными выводами для качественного анализа отсечки электромагнитных волн в ионосфере Земли, когда распространение можно назвать продольным (волна должна бежать вдоль силовых линий магнитного поля Земли).

Качественный характер изменения концентрации свободных электронов в ионосфере по мере подъема над поверхностью Земли приведен на рисунке (точный профиль ионосферы измеряется экспериментально).

Поскольку

пл = √ ∙ 2 ≈ 1,8 ∙ 104 ∙ √ ,0 ∙

т.е. ~пл2 , при фиксированной частоте волны ось абсцисс на рисунке можно разметить в единицах параметра пл2 ⁄ 2.

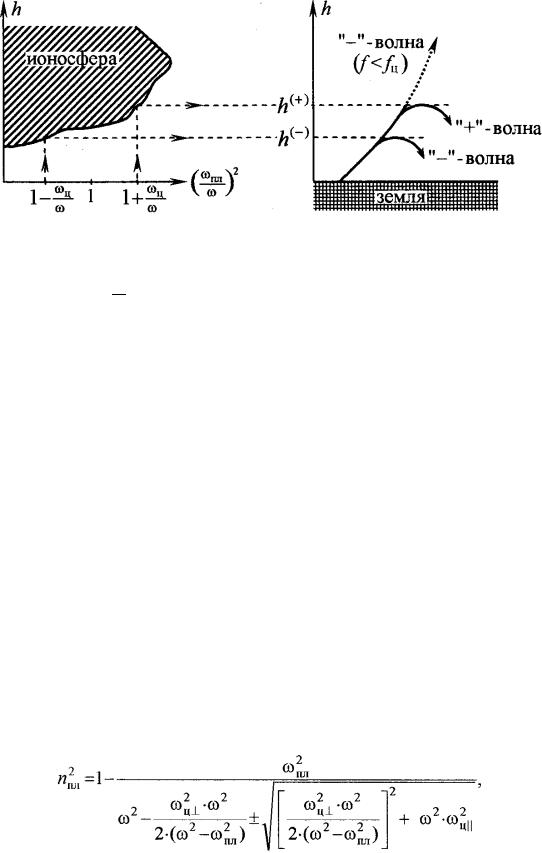
Если принять, что напряженность постоянного магнитного поля

Земли составляет 0 = 40 А/м, то циклотронная частота

ц = 0 ∙ 0 = 2,8 ∙ ∙ 106 −1 и ц = 1,4 МГц.

Если частота плоской линейно-поляризованной волны больше цик-

лотронной частоты ( > ц = 2,8 ∙ 106 −1 и > ц = 1,4 МГц), тогда траектории движения в ионосфере «+» и «–»-волн будут иметь вид, показанный на рисунке слева сплошными кривыми. Отсечка (поворот к Земле) «+» и «–»-волн будет происходить соответственно на разных высотах (+) и (−).

Если частота волны меньше циклотронной < ц, ( < ц), то «+»- волна по-прежнему будет испытывать отсечку на высоте (+), а «–»- волна будет уходить вглубь ионосферы, не возвращаясь к Земле (на рисунке штриховая кривая).

Распространение плоской волны в плазме поперек поля намагничивания

При поперечном распространении (волна по-прежнему бежит вдоль

оси , вектор напряженности поля 0 лежит в плоскости , например, вдоль оси ) угол Θ = 90°, поэтому ц = ц, ц = 0. Подстановка этих значений в

вновь приводит к двойному решению (в знаменателе слагаемое со знаком ±), т.е. распространяющаяся волна разбивается на две волны. Для первой из них (соответствующая верхнему знаку – «+»), она называется обыкновенной,

2пл(об)2 = 1 − пл2 .

Видно, что пл(об) совпадает со значением пл для ненамагниченной (изотропной) плазмы ( ц = ц = 0). В обыкновенной волне для верхнего знака – «–» в выражениях

получим

Таким образом, обыкновенная волна распространяется вдоль осии имеет только одну электрическую составляющую ̇mx(об), параллельную вектору 0. Волна эта ведет себя в плазме так, будто поле0 отсутствует. Поэтому свойства ее не отличаются от свойств плоской линейно-поляризованной волны, бегущей в любом направлении в изотропной плазме. Постоянная распространения и фазовая скорость обыкновенной волны равны соответственно:

(об) = ∙ √ 0 0 ∙ пл(об) = ∙ √ 0 0 ∙ √1 − ( пл⁄ )2,

Обыкновенная волна испытывает отсечку ( пл(об) = 0) при

пл2 = 1.2

Второе решение уравнений Максвелла для задачи о поперечном распространении волн в намагниченной плазме соответствует волне, которую называют необыкновенной. Она соответствует нижнему знаку

– «–» в выражении для пл2

и

В необыкновенной волне для нижнего знака – «+» в выражениях

получим

Следовательно, необыкновенная волна, распространяясь, как и обыкновенная, вдоль оси , имеет две составляющие электрической компоненты ( ̇m(н), ̇my(н)) которые не равны по модулю и сдвинуты по

фазе на 90°. Поэтому вектор ̇(н) необыкновенной волны поляризован

по эллипсу, плоскость которого перпендикулярна 0. Необыкновенная волна характеризуется постоянной распространения

(н) = ∙ √ 0 0 ∙ пл(н)

и перемещается с фазовой скоростью

ф(н) = (н) ,

отличной от скорости движения обыкновенной волны.

Рассмотрим отсечку необыкновенной волны. Приравнивая полученное выражения для показателя преломления пл(н), к нулю,