Электродинамика (РТФ, Климовский, 5 семестр) / Электродинамика .pdf / ЭД (4.4)

4.4. Электромагнитные волны в неоднородных средах

Неоднородность среды может проявляться по-разному: резко, в виде скачка параметров , , , и плавно, когда определенно выраженной границы раздела разных сред не существует. Здесь мы рассмотрим основные особенности распространения волн в безграничной неоднородной среде, характеризующейся плавным изменением показателя преломления. Потерями будем пренебрегать, а среду считать изотропной.

Хорошим примером неоднородной среды является земная атмосфера. В нижней ее части, называемой тропосферой (высота 0...15 км), давление воздуха с увеличением высоты постепенно понижается. Это приводит к уменьшению показателя преломления. В верхней части атмосферы (она называется ионосферой – высота над поверхностью Земли 60...20 000 км) плавное изменение показателя преломления вызвано непостоянством концентрации свободных электронов.

Высотная неоднородность атмосферы оказывает существенное влияние на распространение тропосферных и ионосферных волн.

Для всех видов сред, рассмотренных ранее, общим было свойство строго прямолинейного распространения электромагнитной волны. Посмотрим, по какой траектории будет перемещаться волна в плавнонеоднородной среде. Пусть в направлении оси показатель преломления среды постепенно уменьшается. Разобьем среду на ряд слоев, столь тонких, чтобы в каждом из них с хорошим приближением можно было считать показатель преломления постоянным, а при переходе из нижнего слоя в соседний верхний показатель преломления уменьшался скачком на малую величину ∆.

Предположим, что в первом слое от точки под углом Θ1 к оси распространяется плоская волна. В силу однородности слоя она движется прямолинейно вплоть до самой границы 2-го слоя. В точке волна скачкообразно изменит направление распространения. Связь углов Θ1 и Θ2 определяется вторым законом Снелля:

1 ∙ sinΘ1 = 2 ∙ sinΘ2, 1 = , 2 = − ∆ .

Записанные соотношения справедливы для любой пары смежных слоев, т.е. в каждом слое n ∙ sinΘ = const. Поскольку с ростом номера слоя уменьшается, угол Θ , должен возрастать. В конце концов, волна достигнет такого слоя, на границе которого Θ = 90°. Ясно, что при уменьшении ∆ дискретнослоистая среда постепенно переходит в реальную среду с непрерывным изменением , а кусочно-ломаная траектория волны – в плавно изогнутую траекторию. Вычислим радиус кривизны этой траектории . Из геометрических построений

Учтем, что ∙ sinΘ = const, поэтому полный дифференциал равен нулю

( ∙ sinΘ) = ∙ sinΘ + ∙ (sinΘ) = ∙ sinΘ + ∙ cosΘ ∙ Θ = 0.

Тогда

= −( ⁄ )sinΘ.

Явление отклонения электромагнитной волны от прямолинейного направления распространения в неоднородной среде называется

рефракцией. Таким образом, полученное выражение позволяет вычислить радиус рефракции волны в среде с градиентом показателя преломления ⁄ , если на слой этой среды, характеризующийся показателем , волна упала под углом Θ.

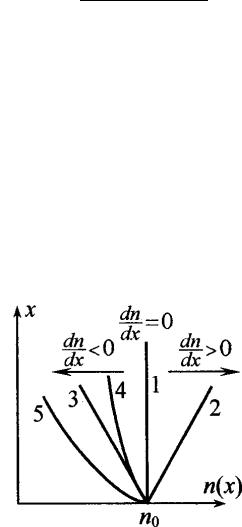
На рисунке приведены примеры рефракции волны, создаваемой источником , для разных законов неоднородности ( ) для различных возможных вариантах изменения показателя преломления неоднородной среды от координаты .

Прямая 1 соответствует однородной среде ( ( ) = 0 = const). Случай 2 описывает среду, в которой с увеличением показатель преломления растет ( ⁄ > 0). Кривые 3, 4, 5 отвечают случаям понижения с ростом ( ⁄ < 0).

Для каждого из указанных вариантов изменения ( ) качественно форма траектории рефракции волны показана на рисунке: 1 – прямолинейная ( = ∞); 2 – круговая ( < 0); 3 – круговая ( p > 0); 4, 5 – криволинейные с положительной рефракцией ( p > 0).

Выражение для радиуса рефракции позволяет вычислить радиус в верхней точке траектории волны при ее распространении в тропосфере. В этом случае Θ → 90°, а ≈ 1. Тогда

Впрактическом отношении интересно рассмотреть случай, когда волна попадает в слой неоднородной среды, показатель преломления которой симметрично уменьшается от середины к краям (см. рисунок).

Втакой среде волна при правильно подобранном угле Θ движется по периодически изогнутой траектории, не доходя до краев слоя. Описанная особенность используется в оптических световодах градиентного типа, придавая им важные преимущества по сравнению со световодами, в которых показатель преломления от середины к краям изменяется скачкообразно.