Электродинамика (РТФ, Климовский, 5 семестр) / Электродинамика .pdf / ЭД (6.9)

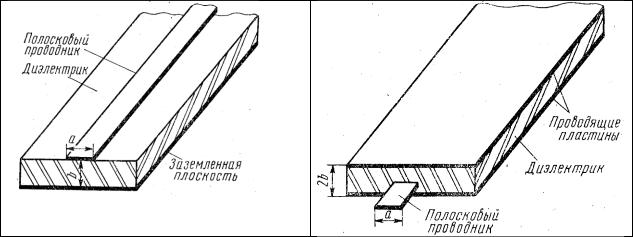
6.9. Электромагнитные волны в полосковой линии

Волна ТЕМ

Полосковая линия, как несимметричная (на рисунке слева), так и симметричная (на рисунке справа), является частным случаем направляющей системы отрытого типа, состоящей из нескольких изолированных друг друга металлических проводников. Следовательно, низший тип волны в этой линии – волна .

Строгий анализ структура полей в полосковой линии весьма сложен. Ограничимся приближенным рассмотрением этого вопроса путем сопоставления полосковой и коаксиальной линий, основанным на том, что полосковую линию в какой-то степени можно рассматривать как деформированную коаксиальную линию.

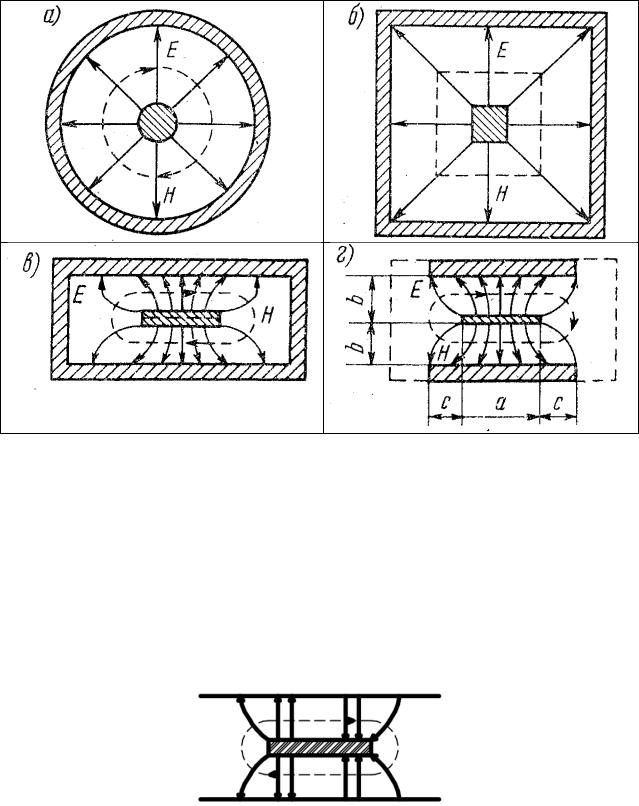
Так как поперечное волновое число у волны равно нулю независимо от размеров и формы поперечного сечения направляющей системы, то при деформации поперечного сечения коаксиальной линии тип волны в ней не меняется. На рисунках а → б → в → г показано, как от коаксиальной линии путем последовательного изменения формы проводников можно прийти к симметричной полосковой линии. На последнем этапе (на рисунке г) узкие боковые стенки внешнего проводника удаляются на бесконечное расстояние

Волны высших типов

Рассмотрим первый высший тип волны в симметричной полосковой линии. Последовательно деформируя поперечное сечение коаксиальной линии, в которой распространяется волна , находим структуру поля первого высшего типа волны (рисунок). Из рисунка видно, что на длине, несколько превышающей ширину центрального проводника полосковой линии, укладывается одна полуволна электрического поля этой волны, т.е. критическая длина этой волны при воздушном заполнении равна λкр≈ 2а.

Волновое сопротивление полосковой линии

Волновое сопротивление полосковой линии определяется таким же методом, как и волновое сопротивление коаксиальной линии.

Приведем только окончательные формулы. Для симметричной полосковой линии

полосковой линии K(k) и K(k') – полные эллиптические интегралы первого рода от аргументов = sch 2 и ′ = th 2 . Формулы для волнового сопротивления получены в предположении, что толщина центрального проводника много меньше расстояния между пластинами.

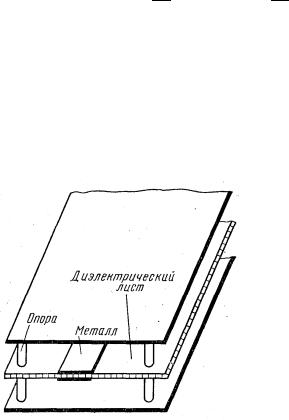
Наиболее распространены полосковые линии, выполненные в виде диэлектрических листов, на поверхность которых приклеиваются или наносятся методами печатного монтажа проводящие пластины.

Диэлектрические листы изготовляются из диэлектрика с малыми потерями (полистирол, фторопласт и др.) С целью уменьшения потерь иногда применяют конструкцию, изображенную на рисунке, в которой электромагнитное поле существует между узким проводником и соответствующей заземленной пластиной. При этом в листе диэлектрика, разделяющем узкие проводники, концентрация энергии весьма невелика и соответственно малы потери. Основными преимуществами полосковой линии перед остальными линиями передачи являются малый вес и габариты, а также простота изготовления: как саму полосковую линию, так и весь полосковый тракт с разнообразными элементами (фильтрами, мостами и др.) можно изготовлять печатным способом.