
Электродинамика (РТФ, Климовский, 5 семестр) / 4.3. ЭМП в волноводах
.pdf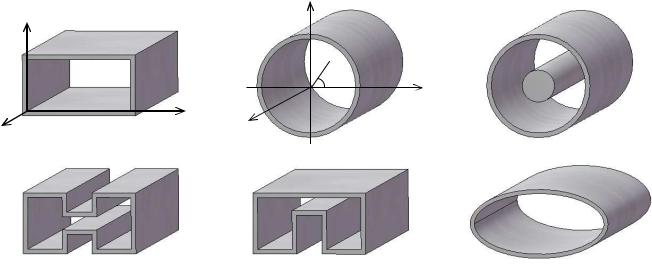
Лабораторная работа № 3. ЭЛЕКТРОМАГНИТНЫЕ ПОЛЯ
ВВОЛНОВОДАХ
3.1.Цель работы
1.Экспериментальное и теоретическое исследование структуры электромаг- нитного поля волны H10 в прямоугольном волноводе.
2.Изучение основных принципов проектирования волноводных устройств.
3.Математическое исследование электромагнитных полей в волноводах с различными поперечными сечениями на основе решений краевых задач электродинамики.
4.Ознакомление с экспериментальными методами измерения компонент электромагнитного поля и характеристик волновых процессов.
3.2.Типы электромагнитных полей в волноводах
Всантиметровом и миллиметровом диапазонах волн в качестве линий передачи электромагнитной энергии широко применяются волноводы, представляющие собой полые металлические трубы различного профиля поперечного сечения, изготовленные из хорошо проводящих материалов, например, меди, алюминия, латуни с серебряным покрытием (рис. 3.1).
Вволноводах невозможно распространение поперечных электромагнитных волн – волн типа T [1]. В них могут существовать только поля электрического и магнитного типов. К полям электрического типа (волны типа E ) относятся такие электромагнитные поля, у которых вектор магнитного поля расположен только в плоскости поперечного сечения волновода, а вектор электрического поля имеет как поперечные, так и продольную составляющую Ez . Если же электрическое поле
полностью поперечно, а магнитное поле имеет также и продольную составляющую Hz , то такие поля называются полями магнитного типа (волны типа H ).
y
y
|
b |
|
|
|
|
|
r . |
x |
|
|
|
|
|
||||
|
|
|
|
|
|
|
ϕ |
|
|
0 |
|
|
|
x |
0 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
z |
|
||
|
|
|
|
|
|
|
|
|
z |
|
|
а) |
a |
|
|
||
|
|
|
|
|
б) |
в) |
||
|
|
|
|
|
|
|
||
г) |
д) |
е) |
Рис. 3.1. Волноводы
32
В конструкциях СВЧ устройств для высоких уровней мощности наиболее широкое распространение получили волноводы прямоугольного и круглого сечений (рис. 3.1, а; 3.1, б), для расширения рабочей полосы частот используют волноводы Н- и П-образного сечения (рис. 3.1, г; 3.1, д), для построения различных устройств используют коаксиальные волноводы (рис. 3, в) и волноводы эллиптического сечения (рис. 3, е).
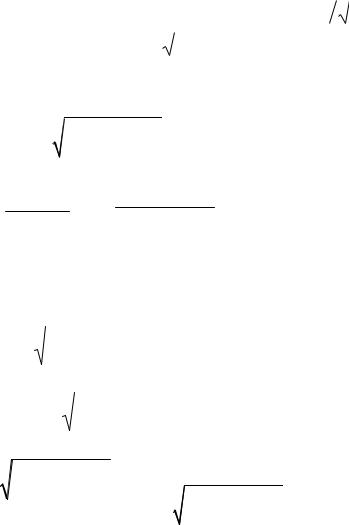
Электромагнитные поля в волноводах существенно отличаются от поперечных волн типа T . Они имеют волновой характер только на частотах выше критической ( f > fкр или ). Продольное волновое число k , определяющее
распространение электромагнитного поля в волноводе, отличается от волнового числа β = 2π / λ для волны типа T , распространяющейся в безграничной среде, имеющей такие же значения абсолютной диэлектрической и магнитной проницаемости среды εa , μa , как и в среде, заполняющей волновод. Кроме того,
волна типа T |
|
скоростью vф = 1 |
|
|
|
характеризуется фазовой |
εaμa |
и |
|||
|
сопротивлением среды Zc = |
|
. Фазовая скорость для |
||
характеристическим |
μa / εa |
||||
волн в волноводе больше фазовой скорости vф волны типа T
vф= |
|
vф |
|
|
|
|
|
1 − (λ / λкр )2 |
|
||
|
|
||
и зависит от частоты. Это значит, что в отличие от волн типа T волны типов E в волноводе обладают дисперсией. Продольное волновое число для волновода
(3.1)
и H
k = 
 β2 − kc2 = β
β2 − kc2 = β 
 1 − (λ / λкр)2 , (3.2)
1 − (λ / λкр)2 , (3.2)
где kc = 2π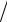 λкр – поперечное волновое число. Длина волны в волноводе всегда больше, чем в безграничной среде:
λкр – поперечное волновое число. Длина волны в волноводе всегда больше, чем в безграничной среде:
λв = |
|
λ |
|
, |
(3.3) |
|
|
|
|
||||
1− (λ / λкр)2 |
||||||
|
|
|
|
|||
а скорость переноса энергии электромагнитного поля меньше:
vгр = vф |
|
. |
|
1 − (λ / λкр)2 |
(3.4) |
Характеристические сопротивления волновода для волн типов E и H :
E |
= Zc |
1 − (λ / λкр ) |
2 |
H |
= |
|
Zc |
|
|
|
|
Zc |
, |
Zc |
|
|
|
. |
(3.5) |
||||
|
|
|
|||||||||
1 − (λ / λкр )2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|||
Поперечные составляющие векторов электромагнитного поля в прямоугольных волноводах можно выразить через продольные компоненты [2]:
|
|
|
поле типа E : |
|
|
|
||||||
E |
x |
= −i |
k |
|
∂Ez |
; E |
y |
= −i |
k |
|
∂Ez |
; |
|
|
|
|
|||||||||
|
|
2 ∂x |
2 |
|
∂y |
|||||||
|
|
|
|
|
||||||||
|
|
|
kc |
|
|
kc |
|
|
|
|||
|
|
|
|
|
поле типа H : |
|
|
|
|
|||
H |
x |
= −i |
k |
|
∂H z |
; H |
y |
= −i |
k |
|
∂H z |
; (3.6, а) |
|
|
|
|
|||||||||
|
2 |
|
∂x |
|
2 |
|
∂y |
|||||
|
|
|
|
|
|
|||||||
|
|
|
kc |
|
|
|
|
|
kc |
|
|
|
33

H x = i ωεa |
∂Ez |
; H y = -i ωεa |
∂Ez |
; |
Ex = -i |
ωμa |
|
∂H z |
; Ey = i |
ωμa |
|
∂H z |
. (3.6, б) |
||||
¶y |
|
|
¶y |
|
|
||||||||||||
k |
2 |
k |
2 |
¶x |
|
k |
2 |
|
|
k |
2 |
|
¶x |
||||
|
c |
|
|
c |
|
|
|
|
c |
|
|
|
|
c |
|
|
|
Заметим, что составляющие поля одного типа формально можно получить из составляющих поля другого типа на основании принципа перестановочной двойственности.
Продольные компоненты Ez и Hz |
определяют из волновых уравнений [2]: |
|
||||||||
|
|
|
|
|
D Ez + kc |
2Ez = 0; |
D H z + kc |
2H z = 0, |
(3.7) |
|
где D = |
¶2 |
+ |
¶2 |
– двумерный оператор Лапласа. Решение волновых уравнений |
||||||
¶x |
2 |
¶y2 |
||||||||
|
|
|
|
|
|
|
||||
(3.7) методом разделения переменных Фурье, удовлетворяющее граничным условиям на идеально проводящих боковых стенках, имеет следующий вид:
E |
z |
= E ×sin |
mπ |
x ×sin |
nπ |
y × e−ikz ; |
(3.8) |
|||||
|
|
|
|
|||||||||
|
0 |
|
|
a |
|
b |
|
|||||
Hz = H0 |
× cos |
mπ |
x × cos |
nπ |
y × e−ikz , |
(3.9) |
||||||
a |
|
|||||||||||
|
|
|
|
|
|
|
b |
|
||||
где E0 , H0 – амплитудные постоянные, |
зависящие от условий |
возбуждения |
||||||||||
электромагнитного поля в волноводе; m, n – |
неотрицательные целые числа, которые |
|||||||||||
называют характеристическими.
Из решения волновых уравнений (3.7) и граничных условий можно определить поперечное волновое число и критическую длину волны в волноводе:
kc = (mp a)2 + (np b)2 ;
(3.10)
lкр = 2  (m
(m a)2 + (n
a)2 + (n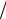 b)2 .
b)2 .
Эти формулы справедливы как для полей типа Е, так и для полей типа Н. Из (3.10) следует, что критическая длина волны тем меньше, чем больше характеристические числа m и n . Подставим в группу соотношений (3.6, а), (3.6, б) выражение (3.8) для нахождения составляющих векторов электромагнитного поля типа H :
Hx = i |
|
|
k |
|
× |
|
mπ |
|
H0 |
×sin |
mπ |
x × cos |
nπ |
|
y × e−ikz ; |
|
|||||||||||||||||||
|
kc |
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|||||
H y = i |
|
k |
× |
np |
|
H0 |
× cos |
mp |
x ×sin |
np |
|
y × e−ikz ; |
|
||||||||||||||||||||||
kc |
2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
(3.11) |
|||||
|
wma |
|
|
|
np |
|
|
|
|
|
|
mp |
|
|
|
np |
|
|
|
−ikz |
|
||||||||||||||
Ex = i |
× |
|
H0 |
× cos |
x |
×sin |
|
y |
× e |
; |
|
||||||||||||||||||||||||
|
kc |
2 |
b |
|
a |
b |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
E y = -i |
wma |
× |
|
mp |
H0 ×sin |
|
mp |
x × cos |
np |
y × e |
−ikz |
. |
|||||||||||||||||||||||
kc |
2 |
|
|
|
a |
|
a |
|
|
|
b |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
34 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Аналогичным образом определяются составляющие векторов для полей типа E . Из формул (3.11) видно, что числа m, n определяют количество стоячих полуволн внутри волновода вдоль координатных осей x и y соответственно. Поскольку характеристические числа m и n могут быть любыми, в прямоугольном волноводе в принципе возможно раздельное существование сколь угодно большого числа волн типа Еmn и Нmn . Подчеркнем, что если одно из характеристических чисел m или n равно нулю для полей Еmn , то все составляющие векторов поля обратятся в нуль, то есть в прямоугольном волноводе не могут существовать поля Еm0 или Е0n . Однако для полей Нmn одно из характеристических чисел может принимать нулевое значение.
Для моделирования структуры электромагнитных полей в прямоугольном волноводе можно использовать текст программы MATLAB, в которой для примера построены силовые линии вектора E волны H11.
function test_rect_wgd
%Построение силовых линий вектора Е волны типа Н
%для прямоугольного волновода.
a=23; b=10;
[x11,y11]=ode15s(@e_hw,[0.01 11.42],4.89); [x21,y21]=ode15s(@e_hw,[0.01 8.0498],3.5); [x31,y31]=ode15s(@e_hw,[0.01 4.6003],2); [x41,y41]=ode15s(@e_hw,[0.01 2.3005],1); [x51,y51]=ode15s(@e_hw,[0.01 1.144],0.5); figure(1); hold on
plot(x11,y11,'b',x21,y21,'b',x31,y31,'b',x41,y41,'b',x51,y51,'b'); line([0 23],[0 0]); line([0 23],[10 10]);
line([0 0],[0 10]); line([23 23],[0 10]);
axis equal; xlim([-0.5 23.5]); ylim([-0.5 10.5]); hold off
function y=e_hw(x,y) a=23; b=10; m=1; n=1;
a1=m*pi/a; b1=n*pi/b; c1=cos(a1*x); c2=cos(b1*y); s1=sin(a1*x); s2=sin(b1*y); y1=a1*s1*c2; y2=b1*c1*s2; y=-y1/y2;
return
function z=h_hw(x,y) a=23; b=10; m=1; n=1;
a1=m*pi/a; b1=n*pi/b; c1=cos(a1*y); c2=cos(b1*x); s1=sin(a1*y); s2=sin(b1*x); y1=a1*s1*c2; y2=b1*c1*s2; z=y1/y2;
return
|
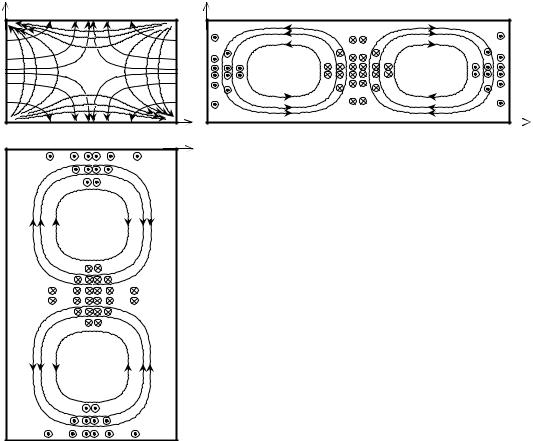
На рис. 3.2, 3.3 изображены картины силовых линий электромагнитного поля |
для |
волн H11, E11 , H10 , распространяющихся в прямоугольном волноводе. |
Структура поля волны H11 играет роль элементарной ячейки при анализе всех более
35
сложных структур, когда m ³1 и n ³1. Например, для волны H21 структура поля в плоскости поперечного сечения может быть получена совмещением двух ячеек
y |
z = 0 |
|
y |
b |
|
|
|
0 |
|
|
x |
y = b |
a |
0 |
|
|
|
||
0 |
|
|
|
|
|
x |
|
|
|
|
z
x = 0
z
В электродинамике и теории антенн принято обозначать силовые линии вектора E сплошными линиями, а вектора H – штриховыми, при этом густота силовых линий пропорциональна амплитуде векторов электромагнитного поля.
Рис. 3.2. Картина силовых линий электромагнитного поля для волны H11
волны H11 по узкой стенке с соответствующим изменением масштаба ячейки по широкой стенке волновода. Аналогично можно построить картины силовых линий и для продольных плоскостей сечения волновода. Для волн типа H1n совмещение ячеек волны H11 будет производиться уже по широкой стенке с таким же соответствующим изменением масштаба ячейки по узкой стенке. Подчеркнем, что такой прием совмещения ячеек по узкой или широкой стенке волновода полностью соответствует граничным условиям для векторов напряженности электрического и магнитного полей (рекомендуется это утверждение проверить самостоятельно).
Решение волновых уравнений для круглого волновода может быть получено аналогично решению для прямоугольного [1]. Из рассмотрения свойств волн Еmn и Нmn прямоугольного волновода следует, что количество вариаций поля по координатам поперечного сечения определяется характеристическими числами m и n . В круглом волноводе эти числа имеют следующий смысл: m означает число вариаций поля по угловой координате ϕ , а n – число вариаций поля по радиальной координате r . Волн, не имеющих вариаций по радиусу (n = 0) , не существует.
36
y b
0
0
z
y b
0
0
z = 0 |
y |
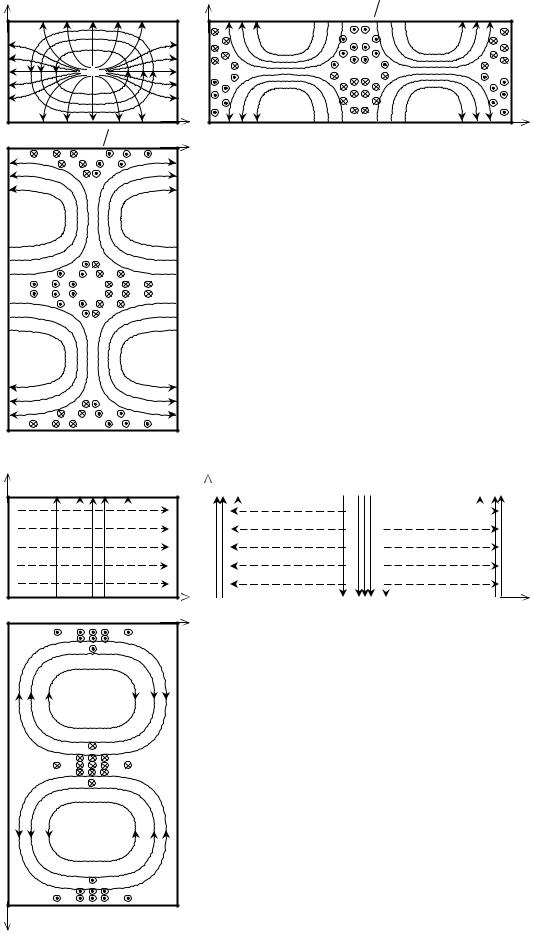
Волна E11 |
x = a 2 |
x |
z |
y = b 2 |
a |
x
z = 0 |
y |
Волна H10 |
x = 0 |
x |
|
z |
|
|
|
y = b |
a |
x
z
Рис. 3.3. Картины силовых линий электромагнитного поля для волн E11 и H10
37
H11
ϕ = π 2
R

 ϕ
ϕ
z
E11 |
ϕ = π 2 |
z
λв  2
2
E01 |
ϕ = π 2 |
|
z
H01 |
ϕ = π 2 |
|
z
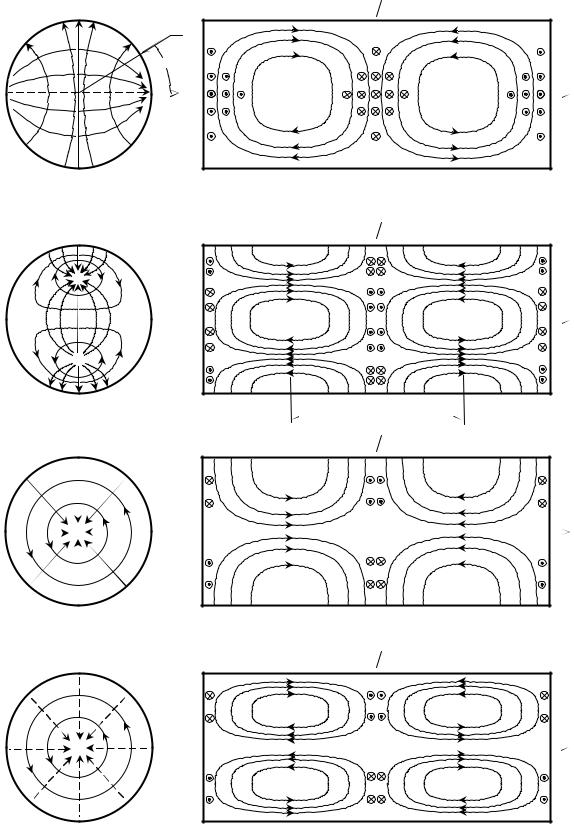
Рис. 3.4. Волны круглого волновода
38
В частном случае m = 0 амплитуды векторов электромагнитного поля не зависят от угловой координаты, подобные типы волн в круглом волноводе называют симметричными.
На рис. 3.4 изображены картины силовых линий электромагнитного поля для некоторых типов волн, распространяющихся в круглом волноводе. Простейшей волной типа Е является волна Е01. Эта волна имеет аналогию с волной Е11 прямоугольного волновода, и вследствие осевой симметрии может использоваться во вращающихся сочленениях – устройствах, в которых одна часть волновода неподвижна, а другая вращается вокруг оси. Также существует определенная аналогия волн Н11 , Е11 круглого волновода с волнами Н10 , Е21 прямоугольного волновода. Важно подчеркнуть, что волна H10 прямоугольного волновода имеет устойчивую поляризацию, а ее аналог – волна Н11 круглого волновода при распространении может легко изменить свою поляризацию вследствие неизбежной эллиптичности поперечного сечения тракта. Это необходимо учитывать при конструировании конкретных волноводных устройств.
Из формул (3.10) следует, что при одинаковых значениях чисел m и n в прямо- угольном волноводе критические длины волн типов Еmn и Нmn совпадают (но m ¹ 0, n ¹ 0 ). В этом случае условия распространения этих волн будут одинаковыми. Волны, имеющие равные критические частоты, называются вырожденными. Смысл этого названия состоит в том, что, например, волна Е11 при небольшой неоднород- ности фидера может легко переходить (вырождаться) в волну Н11, имеющую те же условия существования, но принципиально другую структуру поля. В круглом волноводе вырожденными являются волны Е1n и Н0n с одинаковыми значениями индексов n .
Явление вырождения волн является нежелательным на практике, так как при этом возникает волна с другой структурой поля. Это означает, что устройство отбора энергии из волновода может не возбуждаться, что приводит к снижению коэффициента полезного действия фидера. Для борьбы с этим явлением используют различные фильтры типов волн, основным принципом конструирования которых является введение в волновод дополнительных реактивных элементов (штыри, диафрагмы), нарушающих условия распространения нежелательных типов волн.
3.3. Токи на стенках волновода
Важный практический интерес представляет рассмотрение структуры поверх- ностных токов на металлических стенках волновода, вектор плотности которых определяется из граничных условий следующим образом:
J = n ´ H , |
(3.12) |
где n – вектор единичной внутренней нормали. Плотность поверхностного тока равна по величине тангенциальной компоненте напряженности магнитного поля, а его направление перпендикулярно вектору H .
39
Для волн типа Е магнитное поле имеет только поперечные составляющие. |
||||
Следовательно, для любых волн Еmn поверхностные токи |
протекают только в |
|||
продольном направлении. Волны Нmn около стенок имеют как поперечную, так и |
||||
продольные составляющие магнитного поля, которым соответствуют продольные и |
||||
поперечные токи на стенках волновода. |
|
|
|
|
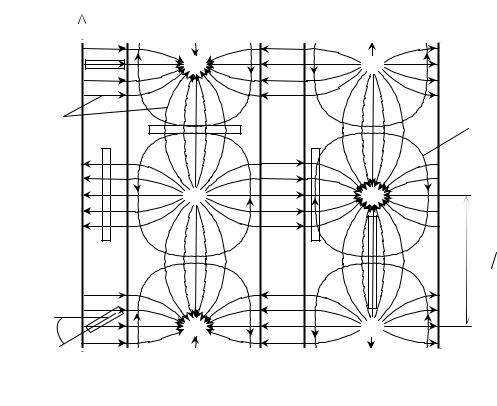
Картину линий поверхностных токов J можно построить с помощью распре- |
||||
деления силовых линий напряженности магнитного поля H . На рис. 3.5 изображена |
||||
картина линий тока на стенках прямоугольного волновода с волной Н10. |
||||
z |
|
|
|
|
1 |
|
|
|
|
J |
4 |
|
H |
|
2 |
5 |
|||
|
|
|||
|
|
6 |
λв 2 |
|
3 |
|
|
|
|
α |
|
|
|
|
Рис. 3.5. Распределение линий поверхностных токов волны Н10 |
||||
В точках, где токи проводимости сходятся или расходятся, они замыкаются через токи смещения jсм = iωεaE , опережающие по фазе векторE на π 2 (силовые линии вектора H для наглядности также приведены на рис. 3.5).
2 (силовые линии вектора H для наглядности также приведены на рис. 3.5).
Заметим, что волна Н01 круглого волновода, обладающая осевой симметрией, характеризуется отсутствием продольных составляющих поверхностных токов. Следовательно, потери в металлических стенках волновода для такой волны минимальны, что позволяет использовать ее в высокодобротных резонаторах, а также для передачи энергии электромагнитного поля на большое расстояние.
Знание величины и направления токов на стенках волновода важно для решения многих практических задач. Например, если в волноводе прорезать щели 2, 3, 4, 5 (рис. 3.5), пересекающие поверхностные токи проводимости, то такие токи будут замыкаться через токи смещения, протекающие между кромками щели и обладающие способностью распространяться в окружающем пространстве. Щель становится источником электромагнитных волн – излучающей антенной. Это свойство щели в волноводе широко используется для построения волноводно- щелевых антенн, устройств возбуждения и связи между волноводами. Для правильного расположения возбуждающей щели необходимо знать распределение
40

токов на стенках волновода для конкретного типа волны. С другой стороны, излучение щели может быть и нежелательным. Излучение щелей, возникающее при неплотном стыке двух волноводов, ухудшает помехозащищенность радиотехни- ческих систем, приводит к потерям передаваемой мощности. При передаче элек- тромагнитных полей с большими уровнями мощности в месте неплотного контакта может возникать искрение, являющееся источником высокочастотных помех. При этом возможно обгорание контактирующих поверхностей, возникающие при этом окислы металлов дополнительно увеличивают потери энергии.
Можно прорезать щель таким образом, что она не будет пересекать линии токов. Например, продольная щель 6 в середине широкой стенки прямоугольного волновода с волной H10 не нарушает условий распространения волны, в нее можно вводить зонды для измерения характеристик поля в волноводе.
3.4. Основные принципы конструирования волноводных устройств
3.4.1. Выбор размеров волновода
Продольное волновое число k , определяющее характер электромагнитного поля в волноводе, будет действительным при λ < λкр . В этом случае поле в
волноводе носит волновой характер, при λ > λкр поле будет экспоненциально
затухающим, так как k будет мнимым.
Реальный волновод имеет конкретные размеры поперечного сечения. Тогда с увеличением характеристических чисел m и n критическая длина волны λкр
уменьшается, а поперечное волновое число kc растет. На основании формулы (3.2) для заданной частоты f = const (или β = const ), начиная с некоторого значения индексов m и n будет выполняться условие kc > β , то есть k будет мнимой величиной. Следовательно, на заданной частоте в конкретном волноводе число распространяющихся типов волн ограничено.
При уменьшении частоты уменьшается и число распространяющихся типов волн. Тогда при достижении определенной частоты в волноводе будет распрос- траняться только один тип волны, имеющий наибольшее значение λкр, который
называется низшим или основным типом волны. Из (3.10) следует, что в прямо- угольном волноводе он соответствует минимальным значениям индексов m и n . Среди волн типа Е наибольшим значением λкр обладает волна Е11 , для которой
λE11 |
= 2ab a2 + b2 , |
(3.13) |
кр |
|
|
а для волн типа Н – волна H10 , для которой
λH10 |
= 2a. |
(3.14) |
кр |
|
|
Так как λHкр10 > λEкр11 , то в прямоугольных волноводах основным типом волны является волна H10 . На рис. 3.6 представлено распределение высших типов волн Е и
41
