Математическое обеспечение САПР (РТФ, Мактас, 5 семестр) / Лабы / Lab_1_P_Rbd-31_Ispr (1)

Министерство науки и образования Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Ульяновский государственный технический университет»

Кафедра: "Конструирование и технологии электронных средств"

Дисциплина: «Математическое обеспечение САПР»

Лабораторная работа №1:

«ИССЛЕДОВАНИЕ ЭФФЕКТИВНОСТИ АЛГОРИТМА ПОКРЫТИЯ СХЕМ МОДУЛЯМИ»

Работу выполнил:

Студент группы Рбд-31

Поляков Т.А.

Проверил:

Мактас М.Я.

Ульяновск 2020

Содержание:

1. Цель работы……………………………………………………….………2

2. Сведения из теории. Задача покрытия, ее математическая формулировка, алгоритм………………………………………………….……2

3. Принципиальная электрическая схема узла и библиотека ИМС....…...5

4. Вектор количественного состава элементов схемы, матрица описания состава модулей ИМС……………………………………,……….……………6

5. Условия покрытия схемы (несколько вариантов)………………………6

6. Результаты решения задачи покрытия…………………………………..7

7. Эскизы схем соединения выводов конструктивных элементов (корпусов ИМС)………………………………………………………………………..…....9

8. Выводы………………………….…………………………………..……..10

Цель работы - исследовать эффективность алгоритма покрытия схем типовых модулей РЭС; усвоить особенности алгоритмизации и программирования задачи покрытия схем на ЭВМ; приобрести навык построения математических моделей объектов конструирования, реализации и исследования их при решении задачи покрытия в САПР.

Общие сведения о задаче покрытия.

Задача покрытия функциональной схемы типовыми модулями из заданного набора является задачей преобразования функциональной схемы в электрическую, т.е. схему соединения конструктивных элементов (резисторов, конденсаторов, транзисторов, интегральных схем, и т.д.) [1-3]. Решается эта задача одной из первых на этапе конструкторского проектирования. Поскольку при проектировании радиоэлектронных средств (РЭС) применяется большое многообразие электрорадиоэлементов (ЭРЭ), то наряду с задачей покрытия часто возникает необходимость определения оптимального набора этих элементов для каждого конкретного класса схемы, минимизация числа типов элементов набора в проектируемом устройстве.

Математическая формулировка задачи.

Исходными данными для решения задачи покрытия являются: функциональная схема устройства и схемы типовых конструктивных элементов используемого набора модулей (интегральных схем, транзисторов, резисторов, конденсаторов, плат и т.д.).

Допустим, схема состоит из множества элементов E = {e₁, e₂,…,e_n} и для каждого из элементов 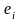известен тип функции F(e_i) (i = 1, 2,…, l), которую он реализует (усилитель, детектор, триггер, схема «И», «ИЛИ» и т.д.).

Набор модулей определяется библиотекой T = {T₁, T₂,…, T_n}.

Количественный состав схемы по типам элементов опишем вектором , в котором b_j – число элементов типа j. Состав модулей библиотеки опишем матрицей , в которой a_kj – число элементов типа j в модуле T_k. Отметим, что элемент схемы может быть реализован с помощью элемента того же типа, находящегося в одном из модулей библиотеки, либо с помощью элементов других типов. Например, элемент ИЛИ с двумя входами может быть реализован элементом ИЛИ с большим числом входов.

Схема считается покрытой модулями из библиотеки T, если каждый элемент схемы реализуется элементами, входящими в состав выбранных модулей.

В качестве критериев оптимальности в задаче покрытия используют:

- суммарную стоимость модулей, покрывающих схему;

- общее число модулей в покрытии;

- число типов используемых модулей;

- число связей между модулями;

- число неиспользованных элементов в модулях.

Ограничениями обычно являются требования на совместную или раздельную компоновку в едином конструктивном модуле элементов функциональной схемы, связанные с обеспечением нормального теплового режима, помехозащищенности и простоты диагностики.

Для оценки качества покрытия используют дополнительный критерий – коэффициент покрытия G = N/M, где N – число элементов в схеме, а M – число модулей (микросхем), которыми покрыта схема.

Рассмотрим наиболее распространенный вариант задачи, в котором критерием качества является суммарная стоимость модулей.

Пусть известны стоимости модулей каждого типа c_1,…, c_k,…, c_m. Если ввести целочисленные переменные x_k , определяющие число модулей типа k, которые необходимы для покрытия с минимальной стоимостью, задача сведется к минимизации функции

(1.1)

при ограничениях

, (1.2)

где j = 1, 2,…,l, a_kj - число элементов типа j в T_k.

Число логических функций любого типа k, входящих во все покрывающие модули, должно быть не меньше общего числа элементов соответствующего типа в реализуемой схеме.

(1.3)

x_k – целое число для всех k, так как любой модуль используется только полностью, независимо от числа задействованных в нем компонентов.

Задача (1.1) – (1.3) является задачей целочисленного программирования.

Целевая функция для минимизации стоимости и числа модулей имеет вид:

,

где r₁ и r₂ – коэффициенты, учитывающие важность используемых критериев.

Принципиальная электрическая схема узла и библиотека ИМС.

Рис.1. Электрическая схема

Рис. 2. Библиотека ИМС

Вектор количественного состава элементов схемы, матрица описания состава модулей ИМС.

Дана электрическая схема, состоящая из t₁, t₂, t₃, t₄, t₅ и t₆ (рис.1.). Существует библиотека ИМС T₁, T₂, T₃ (Рис.2.), причем их условные стоимости равны соответственно: С_Т1=1, С_Т2=2, С_Т3=3 условных единиц стоимости.

Сосчитаем количество элементов каждого типа в схеме: t₁=1, t₂=4, t₃=2, t₄=1, t₅=3, t₆=1 и составим вектор количественного состава:

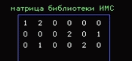
Рис. 3. Матрица описания состава модулей ИМС

Условия покрытия схемы

В качестве критериев оптимальности в задаче покрытия используют:

- суммарную стоимость модулей, покрывающих схему;

- общее число модулей в покрытии;

- число типов используемых модулей;

- число связей между модулями;

- число неиспользованных элементов в модулях.

Результаты решения задачи покрытия:

1) Суммарная стоимость покрытия: 10

Общее число модулей в покрытие: 6

Число неиспользуемых элементов в модулях: 6

Число типов используемых модулей: тип 1 – 3 шт, тип 2 – 2 шт, тип 3 – 1 шт.

Рис. 4. Результат решения №1

С целью найти более оптимальное решение задачи, мной было проведено повторное решение задачи. Имеем вектор количественного состава В0̅ = (2,4,0,2,2,2). Для покрытия выберем микросхему Т1 как наиболее дешевую.

Находим вектор непокрытых элементов В1̅. Для этого из вектора В0̅ поэлементно вычитаем удвоенную строку - 2Т1

_ В0̅ = (2,4,0,2,2,2)

2Т1̅ = (2,4,0,0,0,0)

В1̅ = (0,0,0,2,2,2)

Далее выполним аналогичные действия для микросхемы Т2, стоимость которой больше стоимости Т1 (2>1). Определяем вектор непокрытых элементов В2̅:

_ В1̅ = (0,0,0,2,2,2)

2Т2̅ = (0,0,0,4,0,2)

В2̅ = (0,0,0,-2,2,0)

Далее произведем покрытия оставшихся элементов ИМС Т3 (стоимость - 3). Назначаем 1 шт. Т3:

_ В2̅ = (0,0,0,-2,2,0)

Т3̅ = (0,1,0,0,2,0)

В3̅ = (0,-1,0,-2,0,0)

Процесс покрытия закончен. В итоге, было получено 2 шт. Т1, 2 шт. Т2 и 1 шт. Т3. Коэффициент покрытия схемы G=12/5=2,4. Результат решения задачи приведен на Рис. 5

2) Суммарная стоимость покрытия: 9

Общее число модулей в покрытие: 5

Число неиспользуемых элементов в модулях: 3

Число типов используемых модулей: тип 1 – 2 шт, тип 2 – 2 шт, тип 3 – 1 шт.

Рис. 5. Результат решения №2

Эскизы схем соединения выводов конструктивных элементов (корпусов ИМС).

Результат решения под номером 2 является более дешевым по суммарной стоимости, и имеет меньшее число модулей. Следовательно, создаем эскиз схем соединения выводов конструктивных элементов для этого решения. Рис. 6. Первый вариант соединения корпусов ИМС

Рис. 7. Второй вариант соединения корпусов ИМС

Вывод

При решении задачи покрытия нами был исследован алгоритм покрытия схем типовыми модулями РЭС. В процессе работы на ЭВМ было замечено, что решение, предлагаемое машиной, не всегда является самым экономным, что может потребовать самостоятельного перерасчета количества типовых элементов. Также, решая задачу о соединении элементов между собой, нами был усвоен алгоритм, помогающий сократить число связей между элементами за счет повышения числа связей внутри одного элемента.

Оценивая полученное решение по критериям оптимальности, было получено:

· - суммарная стоимость модулей, покрывающих схему – 9

· - общее число модулей в покрытии – 5

· - число типов используемых модулей – 3

· - число связей между модулями – 9

· - число неиспользуемых элементов в модулях – 3

· - коэффициент покрытия G = 2,4