
Математика спецглавы (РТФ, 3 семестр) / Практика (удаленка) / НСВ хар-ки
.pdf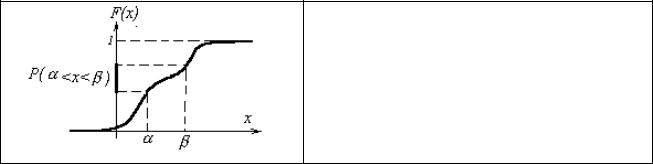
Непрерывные случайные величины
Непрерывной случайной величиной X (НСВ) называется такая вели-
чина, возможные значения которой непрерывно заполняют некоторый интервал (конечный или бесконечный).
Каждому промежутку (а, b) из области значений случайной величины непрерывного типа также отвечает определенная вероятность Р(а < Х < b) того, что значение, принятое случайной величиной, попадет в этот промежуток.
Соотношение, устанавливающее тем или иным способом связь между возможными значениями случайной величины и их вероятностями, называется законом распределения случайной величины.
Интегральный закон распределения
Функцией распределения непрерывной СВ X называется функция F (x) , которая для любого действительного числа x равна вероятности собы-
тия X x :
0, |
|
x x1, |
|
|
|
F ( x), |
x x x |
2 |
, |
||
1 |
|
|
1 |
|
|
|
|
|
x2 x x3, |
||
F ( x) P( X x) F2 |
( x), |
||||
... |
|
|
|
|
|
|
|
|
|
|
|
1, |
x |
n |
x. |
|
|
|
|
|
|
|
|
Функция F (x) существует как для дискретных, так и для непрерывных случайных величин.
Свойства функции распределения:
0 F( x ) 1;
F( ) 0, F( ) 1;
F( x ) – непрерывная функция; F( x ) – неубывающая функция;
P x F( ) F( ).
Дифференциальный закон распределения
Плотностью распределения непрерывной СВ X называется функ-
ция: f ( x ) F' ( x ) .
Плотность распределения указывает на то, как часто СВ появляется в некоторой окрестности т. x при повторении опытов.
График плотности распределения f (x) называется кривой распределе-
ния.
Свойства плотности распределения:
1. f(x) ≥ 0, так как функция распределения является неубывающей.
1
x
2. F (x) f (t)dt , что следует из определения плотности распределе-
ния.
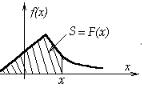
3. Вероятность попадания случайной величины в интервал (а, b) опре-
b
деляется формулой р(а X b) f (x)dx.
a
Геометрически вероятность попадания случайной величины в промежуток (а, b) равна площади соответствующей криволинейной трапеции, ограниченной кривой распределения, осью Ох и прямыми х = а, х = b.
|
|
|
|
4. |
f (x)dx 1 (условие нормировки). |
|
|
|
|
|
|
5. |
lim f (x) 0, |
так как F(x) const |
при x . |
|
x |
|
|
Таким образом, график плотности распределения представляет собой кривую, расположенную выше оси Ох, причем эта ось является ее горизонтальной асимптотой при x (последнее справедливо только для случайных величин, множеством возможных значений которых является все множество действительных чисел). Площадь криволинейной трапеции, ограниченной графиком этой функции, равна единице.
Замечание. Если все возможные значения непрерывной случайной величины сосредоточены на интервале [a, b], то все интегралы вычисляются в этих пределах, а вне интервала [a, b] f(x) ≡ 0.
Иногда функцию f (x) называют дифференциальной функцией распределения вероятности, а функцию F (x) – интегральной функцией рас-
пределения вероятности.
Понятие функции распределения является центральным в теории вероятностей. Используя это понятие, можно дать другое определение непрерывной случайной величины. Случайная величина называется непрерывной, если ее интегральная функция распределения F (x) непрерывна.
Определение и свойства функции распределения сохраняются и для дискретной и для непрерывной случайной величины, для которой функцию распределения можно считать одним из видов задания закона распределения. Но для непрерывной случайной величины вероятность каждого отдельного ее значения равна 0. Это следует из свойства 4 функции распределения: р(Х = а) = F(a) – F(a) = 0. Поэтому для непрерывной случайной величины имеет смысл говорить только о вероятности ее попадания в некоторый интервал.
2

Числовые характеристики непрерывных случайных величин.
Понятие математического ожидания распространяется и на непрерывную случайную величину. Пусть f (x) – плотность вероятности случайной величи-
ны Х. Тогда математическое ожидание непрерывной случайной величины Х
определяется равенством
M ( X ) xf (x)dx
(при условии, что интеграл абсолютно сходится).
Точка оси Ох, имеющая абсциссу, равную математическому ожиданию случайной величины, часто называется центром распределения этой случайной величины.
Дисперсией случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
D(X ) M[X M (X )]2.
Если ввести обозначение М(Х) = т, то формулы для вычисления дисперсии непрерывной случайной величины Х запишутся в виде
|
|
D( X ) (x m)2 f (x)dx. |
|
|
|
Для дисперсии непрерывной |
случайной величины также справедлива |
формула |
|
D( X ) M X 2 M X 2 |
|
или D( X ) x2 f (x)dx M 2 ( X ) |
|
Этой формулой часто пользуются для вычисления дисперсии случайной величины, так как вычисление по этой формуле обычно проще.
Если все возможные значения непрерывной случайной величины не выходят за пределы интервала [a, b], то интегралы в приведенных выше формулах вычисляются в этих пределах.
Средним квадратичным отклонением непрерывной случайной величины
Х называется величина x 
 D( X ).
D( X ).
Среднее квадратичное отношение есть мера рассеяния значений случайной величины около ее математического ожидания.
3

Решение типовых задач
Пример 1. Плотность распределения непрерывной случайной величи-
ны задана формулой |
f (x) |
|
|
C |
|
|
, |
x |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
1 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
Найти: а) значение константы С; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
б) вид функции распределения; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
в) Р(-1 < x < 1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Решение: а) значение константы С найдем из свойства 4: |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||||||||
|
|
dx Сarctgx |
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
C 1, |
откуда |
C |
|
|
|
|
. |
|
|
||||||||||||||||||||||||||||
1 х2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
1 x |
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
б) |
F (x) |
|
|
|
|
|
|
|
dt |
|
|
|
|
arctg |
|
|
t |
|
|
|
|
|
|
|
arctgx |
|
|
|
|
|
|
|
arctgx |
|
. |
|||||||||||||||||||
1 t 2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
1 1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
в) |
p( 1 x 1) |
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
arctgx |
|
|
|
|
|
|
|
0,5. |
|
|
|
|||||||||||||||||||||||||
|
1 x2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
4 4 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример 2. Функция распределения непрерывной случайной величины |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
0, |
|
x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
имеет вид: F (x) |
|
|
|
, |
|
2 x 4 Найти плотность распределения. |
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x 4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 , |
|
|
|
|
|
|
|
|
0, |
x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Решение: f (x) |
|
|
|
|
|
|
|
, 2 x 4 |
0,5, |
2 x 4 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
x 4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Может ли функция |
f (x) |
|
|
|
|
1 |
|
|
|
, |
|
если x 3;3 , |
являться дифференци- |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
9 x2 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||
альной функцией распределения непрерывной СВ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
Решение. Проверим основные свойства 1–2: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
3 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
3 |
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||||||||
1) f (x) dx f (x) dx |
|
f (x) dx f (x) dx 0dx |
|
|
|
|
|
|
|
|
|
dx 0dx |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
3 9 x2 |
3 |
|
|||||||||||||||||||||||||
4
|
1 |
|
|
x |
|
|
3 |
|
|||
|
|
|
|
||||||||
|
arcsin |
|
|
|
|
|
|
||||
|
|
|
|
|
|||||||
|
|
|
3 |
|
|
3 |
|
||||
2) При этом f (x) |
|
1 |
|
|
|
||||||
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
9 x2 |
|
|||||||||
|
|
|
|
|
|||||||
|
1 |
|
|
3 |
|
3 |
|
1 |
|
|
|
|
||
|
|
arcsin |
|
|
arcsin |
|
|
|
|
|
|
|
1. |
|
|
|
|
|
|||||||||||
|
|
|
3 |
|
3 |
|
2 |
|
2 |
|
|
|||
0, если x 3;3 .
Следовательно, данная функция является дифференциальной функцией распределения некоторой непрерывной СВ.
|
0, |
x2 |
x , |
x 1, |
Пример 4. Может ли функция F (x) |
0,5 |
1 x 2 |
||
|
|
|
|
|
|
1, |
|
|
x 2 |
|
|
|
|
|
являться интегральной функцией распределения непрерывной СВ?
Решение. По виду графика функции F (x) име-
ем:
1)0 F(x) 1;
2)F( ) 0, F( ) 1;
3)F (x) – непрерывная функция;
4)F (x) – неубывающая функция.
Свойства интегральной функции распределения выполняются, следовательно, данная функция является интегральной функцией распределения некоторой непрерывной СВ.
Пример 5. |
Задана интегральная функция распределения непрерывной |
|||||||||||||||||||||||||||||||
СВ: F (x) |
1 |
|
1 |
arctg x , x R . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Найти: 1) вероятность, что СВ X примет значения из интервала 0; |
|
|
; |
|||||||||||||||||||||||||||||
|
3 |
|||||||||||||||||||||||||||||||
2) значение СВ x , при котором вероятность P(X ) 0,25. |
|
|
|
|
|
|||||||||||||||||||||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
1 |
|
|
|
|||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
1) P(0 X |
|
3) F (x) |
|
|
|
|
|
|
|
arctg 3 |
|
|
|
|
|
|
|
arctg 0 |
|
|
|
0,3; |
||||||||||
|
0 |
|
|
|
|
2 |
|
|
3 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) P( X ) 0,25 P( X ) 0,25 |
F( ) F( ) 0,25 |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 F ( ) 0,25 |
|
F ( ) 0,75 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
arctg 0,75 |
|
|
1. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример 6. Задана дифференциальная функция распределения непрерывной
|
|
2 |
|
2 |
|
|
|
|
CВ |
f (x) |
|
cos |
|
x , x |
|
; |
. |
|
|
|
||||||
|
|
|
|
|
2 |
|
2 |
5

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
||
Найти вероятность того, что СВ X примет значения из интервала |
0; |
|
. |
|||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
2 |
2 |
|
|
2 |
|
|
|
3 4 |
|
|
|
2 2 |
|
2 |
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|||||||||
P 0 X |
|
|
|
|
|
|
cos |
|
x |
dx |
0 dx |
|
|
|
cos |
|
x |
dx |
|
|
|
1 cos 2x dx |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
4 |
|
0 |
|
|
|
|
|
|
2 |
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
2 |
|
1 |
|
|
|
|
1 |
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
x |
|
|
sin 2x |
|
|
|
|
|
|
0 |
|
|
sin |
|
|
|
sin0 |
|
|
. |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
0 |
|
2 |
|
|
2 |
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Пример 7. Задана интегральная функция распределения непрерывной
СВ F (x) 1 1 2
Решение.
arctg x , x R . |
Найти числовые характеристики. |
|
f (x) F ' (x) |
1 |
, x R. |
1 x2 |
||
|
|
|
|
|
|
|
|
1 |
|
|
1 |
ln 1 x2 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
1) M [ X ] x f (x) dx x |
2 dx |
|
0 ; |
|
|
|
|
|
|
|
|||||||||||||||||
1 x |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
2 |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
2) D [ X ] M [ X mX 2 ] M [ X 0 2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
] M [ X 2 ] |
|
|
x2 f (x) dx |
|
|
|
x2 |
|
dx |
||||||||||||||||||
|
|
|
1 x2 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
|
x |
2 |
1 1 |
|
2 |
|
1 |
|
|
|
|
2 |
x arctg x |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
dx |
1 |
|
|
dx |
|
|
|
|
. |
|
|
|||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
1 x |
|
|
|
0 |
1 x |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Пример 8. |
|
Случайная величина X задана функцией распределения |
|
||||||||||||||||||||||||
|
|
0; |
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
0 x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
F x x3; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Найти: 1) вероятность попадания случайной величины X в интервал (1/3; 2/3); 2) функцию плотности вероятностей f (x); 3) математическое ожидание случайной величины X.
Решение.
1) Вероятность попадания случайной величины в интервал (a, b)
равна
P (a < X < b) = F (b) – F (a)
P (1/3 < X < 2/3) = F (2/3) – F (1/3) = (2/3)3 – (1/3)3 = 8/27 – 1/27 = 7/27
2)Функция плотности
|
|
0; |
|
x 0 |
|
|
|
2 |
0 x 1 |
|
|
|
||
f x F x 3x ; |
||||
|
|
0; |
x 1 |
|
|
|
|||
3)Математическое ожидание
6

M x |
|
|
1 |
1 |
x |
4 |
|
1 |
|
3 |
||
|
|
|
||||||||||
|
xf (x)dx |
= |
|
x 3x2dx = 3 x3dx = 3 |
|
|
|
|
|
|||
|
|
|
|
|
|
|||||||
|
|
|
|
4 |
|
|
|
4 |
||||
|
|
|
0 |
0 |
|
|
0 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 9. Случайная величина имеет равномерное распределение на отрезке [2, 6], ее плотность вероятности имеет вид:
f(x) = C, |
x [2,6] |
|
x [2,6] |
||
0, |
Найти: 1) константу С; 2) основные числовые характеристики: математическое ожидание, дисперсию, среднее квадратичное отклонение; 3) вероятность попадания данной случайной величины в интервал (-1,4).
1) Постоянную С можно определить из условия нормировки:
|
b |
|
|
|
b |
|
f (x)dx = |
|
f ( x)dx = С dx = С(b – a) = 1, откуда |
||||
|
a |
|
|
|
a |
|
С = 1/(b - a)= |
1 |
|
1 |
. |
||
6 2 |
4 |
|||||
|
|
|
|
|||
Поэтому выражение для f (x) можно переписать в следующем виде:
|
|
|
|
|
f (x) = 1 / 4, |
x [2,6]. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
0, |
|
|
x [2,6] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2) Математическое ожидание |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
M X |
|
|
|
|
1 6 |
|
|
1 x2 |
|
|
|
1 |
|
62 |
|
|
|
22 |
|
|
1 36 |
|
4 |
|
|
1 |
18 |
2 4 . |
|||||||||||||||||||
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
xf (x)dx = |
|
|
xdx |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
4 2 |
|
|
4 2 |
|
|
4 |
|
2 |
|
|
2 |
|
|
|
|
4 2 |
|
2 |
|
4 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Дисперсия D X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
x2 f (x)dx M [ X ] 2 = |
|
x |
2dx |
16 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
4 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 x3 |
|
|
1 |
|
63 |
|
|
23 |
|
|
|
|
|
1 |
216 |
|
|
|
8 |
|
|
|
|
|
|
1 |
108 4 16 26 16 10 |
|||||||||||||||||||
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
= |
|
|
|
|
2 |
16 |
|
|
|
|
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
16 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
4 3 |
|
|
4 |
|
3 |
|
|
3 |
|
|
|
|
|
4 |
2 |
|
|
|
|
2 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
.Среднее квадратичное отклонение 
 D[ X ]
D[ X ] 
 10 .
10 .
3) Вероятность попадания случайной величины в интервал (-1,4). Найдем функцию распределения данной случайной величины:
|
|
|
x |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a) пусть x 2 , тогда F (x) |
f (x)dx 0dx 0 ; |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
x |
|
2 |
|
|
x |
|
1 |
|
|
1 |
x 2 ; |
||||
б) пусть |
x [2,6], |
тогда |
F (x) |
f (x)dx |
0dx |
|
dx |
|||||||||||
4 |
4 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||
|
x 2, тогда |
|
x |
2 |
|
|
|
6 |
1 |
|
x |
|
|
|||||
в) пусть |
F (x) |
f (x)dx |
|
0dx |
|
|
dx |
0dx 1. |
|
|||||||||
4 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
6 |
|
|
|
|
|
|||
Вероятность попадания в |
интервал |
(-1,4) |
|
рассчитаем |
по формуле |
|||||||||||||
p X F( ) F( ) F(4) F( 1) |
1 |
(4 2) 0 |
1 |
. |
|
|
||||||||||||
|
|
|
|
|||||||||||||||
|
|
|
|
|
4 |
|
|
|
|
2 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|

Пример 10. Плотность распределения случайной величины Х имеет
вид:
|
0, x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x2 6x 8), 2 x 4 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
f ( X ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0, x 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Требуется найти М(Х), D(X), σ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
4 |
|
|
|
|
|
3 |
x4 |
|
6x3 |
|
8x2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|||||||||||||||
Решение: M ( X ) |
|
|
x(x2 6x 8)dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3; |
|||||||||||||||
4 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
4 |
|
|
|
3 |
|
|
|
2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
4 |
|
2 |
x |
2 |
6x 8 dx 9 |
3 |
x5 |
6x4 |
|
|
|
8x |
3 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
4 |
|
|
|
|
||||||||||||||||||||||
D( X ) |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
9 0,2 ; |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
4 |
2 |
|
|
|
|
|
|
|
|
4 |
|
5 |
|
|
4 |
|
|
|
|
3 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
0,2 0,447 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Пример 11. Случайная величина Х задана функцией плотности вероят-
ности
0, ïðè x 0
f ( x) õ , ïðè 0 x 2
2
0, ïðè x 2
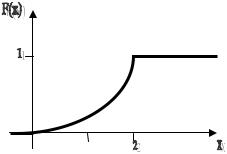
Найти функцию распределения F(x) случайной величины Х. Построить графики функций f(x) и F(x). Вычислить М(Х) (математическое ожидание) и дисперсию D(X).
Решение
Построим график функции f(x):
Функция F(x) распределения непрерывной случайной величины Х
найдем по формулам: F(x)= f ( x)dx .
Если случайная величина Х принимает все свои возможные значения в
â |
0 |
|
(а, в), то f ( x)dx 1. |
Поэтому если х<0, то F(x)= 0 |
dx 0 . |
à |
|
|
8
|
|
|
|
|
|
0 |
|
|
x |
x |
|
|
x2 |
|
|
|
|
|
|
|
|
|
Если 0 х 2, то F(x)= |
0 dx |
|
dx |
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 |
4 |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
0 |
|
2 |
x |
|
|
|
|
|
|
x |
2 |
|
02 |
|
1 |
22 |
02 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Если х>2, то F(x)= |
0 dx |
dx |
0 dx |
|
|
|
||||||||||||||||
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
0 2 |
|
|
2 |
|
|
|
4 |
|
|
|
4 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Итак, искомая интегральная функция имеет вид: |
|
|
|
|
||||||||||||||||||
0, |
ïðè |
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
F ( x) |
|
|
, |
ïðè |
0 x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4 |
|
x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1, |
|
|
ïðè |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Построим ее график:
Математическое ожидание М(Х) и дисперсию D(X) вычислим по формулам:
|
|
|
M ( Õ) |
x f (x)dx; |
если все возможные значения Х (à, â), то |
|
|
|
â
M ( Õ) f (x)dx.
à |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
D( Õ) |
|
(x M (x))2 |
f (x)dx или |
|
|
|
|
D( Õ) |
x2 f (x)dx (M ( Õ))2 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
â |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если Х (à, â), то D( Õ) x2 f (x)dx (M ( Õ))2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
à |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
x |
|
|
1 |
2 |
|
|
|
|
|
1 |
|
x |
3 |
|
2 |
1 |
23 |
|
|
|
|
8 |
|
|
4 |
|
|
|
1 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
M ( Õ) |
|
x |
|
dx |
|
x2dx |
|
|
|
|
03 |
|
1 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
0 |
|
|
|
|
2 |
|
2 |
0 |
|
|
|
|
|
2 |
3 |
0 |
|
6 |
|
|
|
|
|
|
|
|
6 |
|
|
3 |
|
|
|
3 |
|
|
|
|||||||||||||||||||
|
|
2 |
|
|
2 |
|
|
|
x |
|
4 2 |
|
1 |
|
2 |
3 |
|
|
|
|
|
16 |
|
|
|
1 |
|
1 |
|
4 |
|
|
|
16 |
|
|
|
|
1 |
|
|
|
16 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
D(x) x |
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
x dx |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
0 |
|
|
|
|
|
|
2 |
|
|
3 |
|
|
2 |
|
0 |
|
|
|
|
|
|
|
9 2 4 |
|
|
0 |
|
|
9 |
|
|
|
|
8 |
|
|
|
9 |
|
||||||||||||||||||
|
1 |
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
16 |
|
|
|
|
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
8 |
|
|
9 |
|
|
|
|
|
|
72 |
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример 12. Дана функция плотности распределения
9
0, |
x 0, |
|
|
f (x) A(x 2), 0 x 2, |
|
|
x 2. |
0, |
|
Найти: 1) параметр А; 2) построить графики плотности вероятности и функции распределения; 3) Р(1 < x < 4); 4) М(Х), D(X), (X); 5) вероятность того, что отклонение случайной величины Х от М(Х) будет не более 1.
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||
Решение. Так как |
|
|
f (x)dx 1 , получаем A(x 2)dx 1 , то есть |
|||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
||||
2 |
|
(x 2)2 |
|
|
2 |
|
|
1 |
|
|||||
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
||||||||
A(x 2)d (x 2) A |
|
|
A(8 2) 6 A , |
и 6A 1 A |
. |
|||||||||
|
2 |
|
|
|||||||||||
|
|
|
|
|
6 |
|||||||||
0 |
|
|
|
|
|
|
0 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
0, |
|
x 0 |
|
|
|
|
||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Итак, |
f (x) |
|
|
(x 2), |
0 x 2 |
|
|
|
||||||
6 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
x 2. |
|
|
|
|
||||||
|
|
0, |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найдем F(х), функцию распределения по формуле
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F (x) f (t)dt : |
|
|
|
если |
x 0 , |
|
|
F (x) |
0dt 0 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0 x 2 |
|
|
F (x) |
0 |
0dx x |
1 |
|
(t 2)dt |
x2 |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
если |
|
, |
|
6 |
|
|
3 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
x2 |
|
x |
|
2 |
|
|
|
4 |
|
|
|
2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
если 2 x , |
|
F (x) |
0dx |
(x 2)dx 0dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
12 |
3 |
|
|
12 |
|
3 |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
6 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0, |
|
x 0 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F (x) |
x2 |
|
|
, |
0 x |
2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Итак, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1, |
x 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Найдем P(1 < x < 4). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Так как P(х1 < x < х2) = F(х2) – F(х1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
x2 |
x |
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
F (1) |
|
|
|
|
|
|
|
|
|
, |
F(4) = 1, |
|
P(1 < x < 4) = 1– |
|
. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
12 |
3 |
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
x 1 |
|
12 |
12 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Найдем М(X) по формуле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
1 x3 |
|
|
2x2 |
|
2 |
|
10 |
|
. |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
M ( X ) |
|
|
|
|
|
|
|
|
|
|
M ( X ) |
|
|
|
|
|
x(x 2)dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
xf (x)dx |
|
|
6 |
|
|
|
6 |
|
|
3 |
|
|
2 |
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Дисперсия вычисляется по формуле
10
