Случайной величиной называется переменная, которая может принимать те или иные значения в зависимости от различных обстоятельств, и случайная величина называется непрерывной, если она может принимать любое значение из какого-либо ограниченного или неограниченного интервала.
Итак,
функцией распределения случайной
величины (как дискретной, так и непрерывной)
или интегральной
функцией
называется функция
,
которая определяет вероятность, что
значение случайной величины X
меньше или равно граничному значению
х.
Плотностью вероятности f(x) непрерывной случайной величины называется производная её функции распределения:
.
Зная функцию плотности, можно найти вероятность того, что значение непрерывной случайной величины принадлежит закрытому интервалу [a; b]:
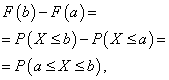
вероятность того, что непрерывная случайная величина X примет какое-либо значение из интервала [a; b], равна определённому интегралу от её плотности вероятности в пределах от a до b:
или
.
При этом общая формула функции F(x) распределения вероятностей непрерывной случайной величины, которой можно пользоваться, если известна функция плотности f(x):
.
График плотности вероятности непрерывной случайной величины называется её кривой распределения (рис. ниже).
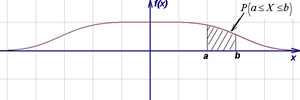
Площадь фигуры (на рисунке заштрихована), ограниченной кривой, прямыми, проведёнными из точек a и b перпендикулярно оси абсцисс, и осью Ох, графически отображает вероятность того, что значение непрерывной случайной величины Х находится в пределах от a до b.
Свойства функции плотности вероятности непрерывной случайной величины
1.
Вероятность того, что случайная величина
примет какое-либо значение из интервала
(и площадь фигуры, которую ограничивают
график функции f(x)
и ось Ох)
равна единице:
2. Функция плотности вероятности не может принимать отрицательные значения:
,
а за пределами существования распределения её значение равно нулю
Плотность распределения f(x), как и функция распределения F(x), является одной из форм закона распределения, но в отличие от функции распределения, она не универсальна: плотность распределения существует только для непрерывных случайных величин.
Упомянем о двух важнейших в практике видах распределения непрерывной случайной величины.
Если функция плотности распределения f(x) непрерывной случайной величины в некотором конечном интервале [a; b] принимает постоянное значение C, а за пределами интервала принимает значение, равное нулю, то такое распределение называется равномерным.
Если график функции плотности распределения симметричен относительно центра, средние значения сосредоточены вблизи центра, а при отдалении от центра собираются более отличающиеся от средних (график функции напоминает разрез колокола), то такое распределение называется нормальным.
Пример 1. Известна функция распределения вероятностей непрерывной случайной величины:
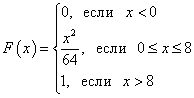
Найти
функцию f(x)
плотности вероятности непрерывной
случайной величины. Построить графики
обеих функций. Найти вероятность того,
что непрерывная случайная величина
примет какое-либо значение в интервале
от 4 до 8:
.
Решение. Функцию плотности вероятности получаем, находя производную функции распределения вероятностей:
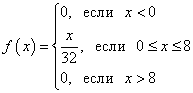
График функции F(x) - парабола:
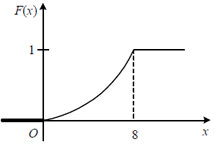
График функции f(x) - прямая:
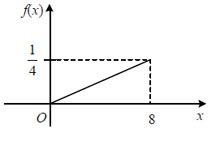
Найдём вероятность того, что непрерывная случайная величина примет какое либо значение в интервале от 4 до 8:
.
Характеристики равномерного распределения
Характеристики равномерного распределения:
среднее значение (математическое ожидание)
;
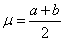дисперсия
;
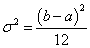стандартное отклонение
;
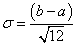равномерное распределение не имеет моды.
Решение примеров на равномерное распределение
Пример 1. Наблюдения показали, что вес ящика, предназначенного для транспортировки овощей, является равномерно распределённой случайной величиной в интервале от 985 г. до 1025 г. Случайно выбран один ящик. Найти характеристики равномерно распределённой случаной величины при условиях, которые будут указаны в решении.
Решение. Найдём вероятность того, что вес данного ящика будет в интервале от 995 г. до 1005 г. :
.
Найдём среднее значение непрерывной случайной величины:
.
Найдём стандартное отклонение:
.
Определим,
у скольки процентов ящиков вес находится
на удалении одного стандартного
отклонения от среднего значения (т. е.
в интервале
):
.
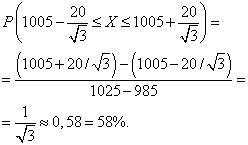Пример 2. Поезда метрополитена идут регулярно с интервалом 2 (мин.). Пассажир выходит на платформу в случайный момент времени, никак не связанный с расписанием поездов. Случайная величина T - время, в течение которого ему придётся ждать поезда, имеет равномерное распределение. Найти плотность распределения f(x) случайной величины T, её математическое ожидание, дисперсию и стандартное отклонение. Найти вероятность того, что ждать придётся не больше полминуты.
Решение. Найдём плотность распределения f(x):
f(x) = 1/2 (0 < x < 2).
Найдём математическое ожидание случайной величины:
μ = (2 + 0)/2 = 1.
Найдём дисперсию:
σ² = 2²/12 = 1/3.
Стандартное отклонение:
σ = (√3)/3.
Найдём вероятность того, что пассажиру придётся ждать поезда не больше полминуты:
P{T < 1/2} = 1/4.
Пример 3. Случайная величина X распределена равномерно на участке (a, b). Найти вероятность того, что в результате опыта она отклонится от своего математического ожидания больше, чем на 3σ.
Решение. Найдём стандартное отклонение:
σ = (b - a)/(2√3);
3σ = 3(b - a)/(2√3) = √3(b - a)/2;
При равномерном распределении на участке (a, b) крайние точки a и b, ограничивающие участок возможных значений случайной величины, отстоят от её математического ожидания μ = (a + b)/2 на расстояние (b - a)/2, которое меньше, чем √3(b - a)/2. Следовательно, вероятность события, обозначенного в условии задачи, равна нулю.