Задача 1

Случайные величины  и  независимы и распределены равномерно.  -в интервале ,  -в интервале . Найти математическое ожидание случайной величины .

Решение:

Воспользуемся свойствами математического ожидания:

Ответ:

Дисперсия и ее свойства. Среднее квадратическое отклонение

Дисперсией называется математическое ожидание квадрата отклонения случайной величины  от :

Стандартное (среднее квадратичное) отклонение случайной величины  определяется как корень из дисперсии и обозначается

Для вычисления дисперсии на практике удобно пользоваться следующей формулой:

Дисперсия равна разности между математическим ожиданием квадрата случайной величины  и квадратом ее математического ожидания.

Изучение переменных факторов по их дисперсиям называется методом дисперсионного анализа.

Свойства дисперсии

Свойство 1.

Свойство 2. Дисперсия константы равна нулю:

Свойство 3. Постоянный множитель выносится из-под знака дисперсии в квадрате:

Свойство 4. Дисперсия суммы случайных величин:

где   – ковариация  случайных величин  и

В частности, если  и  независимы, то

Прибавление константы  в случайной величине не меняет ее дисперсии:

Дисперсия разности равна сумме дисперсий:

Задача 1

Даны законы распределения независимых случайных величин  и :

	0	1
	0.4	0.6

 

и

	2	3
	0.5	0.5

Найти закон распределения суммы . Проверить равенство

Решение:

Распределение суммы :

	0+2	0+3	1+2	1+3

Окончательно получаем:

	2	3	4	Итого
	0.2	0.5	0.3	1

 

Вычислим математические ожидания:

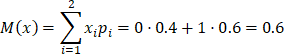
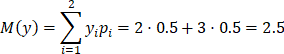
Вычислим дисперсии:

Проверим равенство :

Равенство выполняется.

Задача 2

Вероятность изготовления бракованной детали на первом станке составляет 3%, на втором станке 5%. На первом станке было изготовлено 20 деталей, на втором 40 деталей. Найти математическое ожидание и дисперсию числа бракованных деталей.

Решение:

Математическое ожидание биномиального распределения:

Дисперсия:

Математическое ожидание величины  – числа бракованных деталей на 1-м станке:

Дисперсия:

Математическое ожидание величины  – числа бракованных деталей на 2-м станке:

Дисперсия:

Математическое ожидание числа бракованных деталей:

Дисперсия числа бракованных деталей:

Ответ: ;