Закон распределения дискретной случайной величины.

Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.

Простейшей формой закона распределения дискретной случайной величины является ряд распределения.

Величина, которая может принимать только конечное или счетное множество значений, называется дискретной. Значение дискретной случайной величины можно записать в виде конечной или бесконечной последовательности  Если для каждого из этих значений  определить соответствующую вероятность

то мы получим ряд распределения данной случайной величины:

Значения			…
Вероятности			…

Чтобы последняя таблица была таблицей распределения случайной величины, должны выполняться два требования:

1)  (вероятности не могут быть отрицательными величинами)

2)

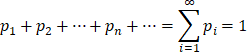
Если  принимает конечное число значений, то такая дискретная случайная величина называется конечной.

Функцией распределения случайной величины  называется функция , определенная для любого действительного  и выражающая вероятность того, что случайная величина  примет значения, меньшее :

Функция распределения обладает следующими свойствами:

1) Для любого  справедливо неравенство

2) Функция распределения является неубывающей функцией, т.е. если , то

3) Вероятность того, что случайная величина примет значения из полуинтервала  равна разности значений функции распределения на концах, то есть:

4) Справедливо равенство:

5) Справедливы следующие предельные соотношения:

6) Функция распределения непрерывна слева, то есть

Математическим ожиданием, или средним значениям,  дискретной случайной величины  называется сумма произведений всех ее значений на соответствующие им вероятности:

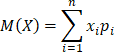
Дисперсией  случайной величины  называется математическое ожидание квадрата ее отклонения от математического ожидания:

Средним квадратическим отклонением (стандартным отклонением, стандартом)  случайной величины  называется арифметическое значением корня квадратного из ее дисперсии:

1. Задачи по дсв

2. Пример 1

3. Задан закон распределения дискретной случайной величины

   х	-1	3	6	7	8
   р	0,1	0,4	0,3	0,1	0,1

5. Построить многоугольник распределения, график функции распределения, найти математическое ожидание и дисперсию

6. Найти вероятность Р{ 3<=X<7}

7. РЕШЕНИЕ

8. Многоугольник распределения

9. 

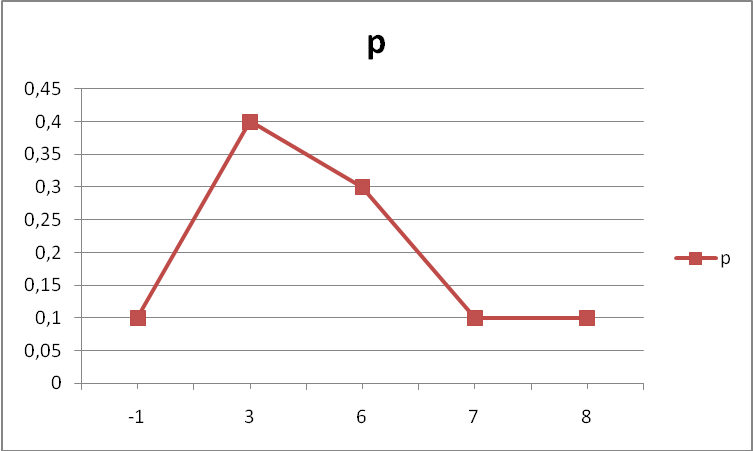
10. F(-1)=P{X<-1}=0

11. F(3)=P{X<3}=0,1

12. F(6)=P{X<6}=0,1 +0,4=0,5

13. F(7)=P{X<7}=0,1 + 0,4 + 0,3 =0,8

14. F(8)=P{X<8}=0,1 + 0,4 + 0,3 +0,1=0,9

15. F(10)=P{X<10}=0,1 + 0,4 + 0,3 +0,1 +0,1=1

16. Построим график функции распределения

19. 

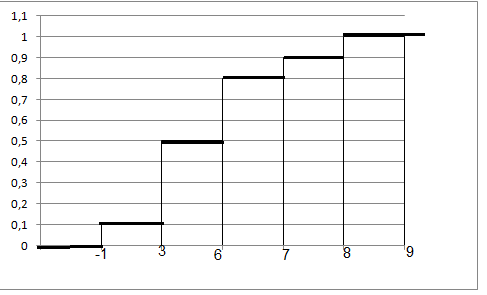
20. m_x=-1*0.1+3*0.4+6*0.3+7*0.1+8*0.1=4,4

21. D_x=m_x² –m²_x =(-1)² *0.1 + 3²*0.4+6²*0.3+7²*0.1+8²*0.1 - 4,4²=25,8-19,36=6,44

23. Р{ 3<=X<7}= F(7) - F(3)=0,8-0,1=0,7

26. Пример 2

    х	1	3	5	7	9
    р	0,25	0,2	0,15	?	0,15

28. Построить многоугольник распределения, график функции распределения, найти математическое ожидание и дисперсию

29. Найти вероятность Р{ 2<=X<7}