4.2 Принцип измерения координат отражателей. Угол ввода луча

Принцип измерения координат отражателей состоит в измерении временного интервала T от момента излучения до момента приема сигнала от дефекта и в пересчете его в координаты по известной скорости распространения волны, с учетом времени распространения ультразвука в призме преобразователя t_п и угла α озвучивания дефекта (рис. 4.1). Координаты всегда определяются по методу максимума, т. е. при положении преобразователя, соответствующем максимуму амплитуды эхосигнала. Для определения координат в дефектоскопах имеется отдельный функциональный блок – глубиномер. В большинстве случаев кроме Н_д и L_д измеряется r.

Формулы для расчета координат следующие:

при  = 0º Н_д = С_l (см. рис. 4.1, а); (4.1)

при   0 Н_д = С_t cosα; (4.2)

L_д = С_t sinα (см. рис. 4.1, б). (4.3)

а) б)

Рис. 4.1. Принцип измерения координат отражателя при контроле прямым (а)

и наклонным (б) преобразователем

Для расчета по приведенным формулам необходимо знать угол озвучивания, при котором амплитуда эхосигнала от дефекта достигает максимума. Чтобы исключить влияние дефекта, такой угол, называемый углом ввода, определяют для ненаправленного отражателя. Угол ввода луча – это угол между нормалью к поверхности, на которой установлен преобразователь, и линией, соединяющей центр цилиндрического отражателя с точкой выхода, при установке преобразователя в положение, при котором амплитуда эхосигнала наибольшая.

Фактический угол ввода α₁, определенный таким образом, отличается от угла наклона _С, вычисленного по формулам Снеллиуса (рис. 4.2).

Отклонение ₁ от _С всегда происходит в сторону угла преломления, соответствующего максимальному коэффициенту прозрачности границы «призма – металл». Оно тем существеннее, чем меньше направленность поля поперечной волны.

Необходимость измерения координат связана с необходимостью исправления дефекта (при этом, конечно, важно точно определять истинное местоположение дефекта) и проблемой отстройки от ложных сигналов (от конструктивных отражателей, донной поверхности, допустимых подрезов и пр.). В связи с этим актуальна минимизация погрешности измерения координат. Рассмотрим подробнее ее составляющие.

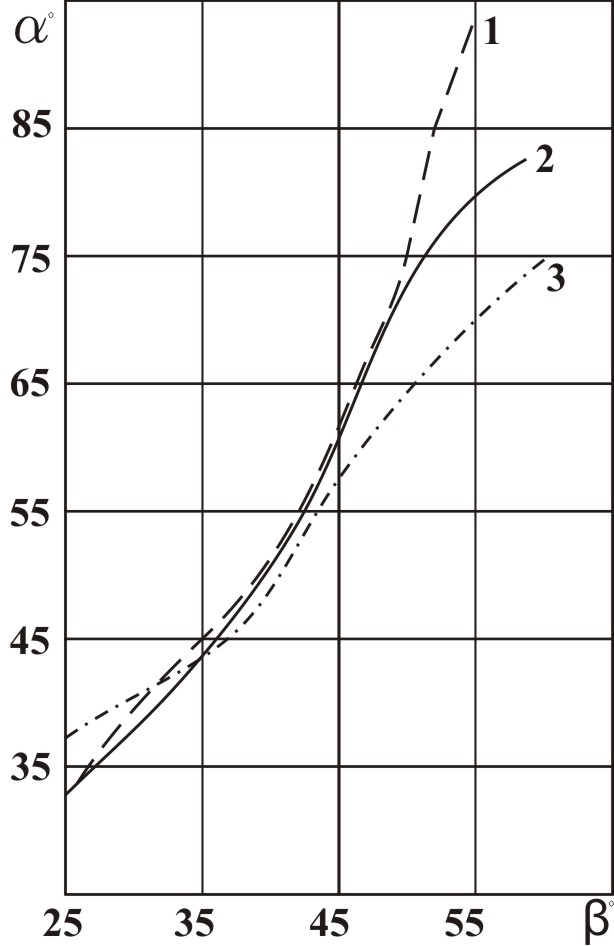
Рис. 4.2. Зависимость угла наклона акустической оси диаграммы направленности поля поперечной волны в сталь (₁) и угла преломления по Снеллиусу (1) от угла призмы (β) преобразователя из оргстекла при af = 5 мм · МГц (3) и 15 мм · МГц (2)

4.3 Случайные и систематические погрешности измерения координат

Случайные погрешности описываются законами теории вероятности и математической статистики, имеют случайный характер и могут быть уменьшены с увеличением числа измерений, дальнейшим усреднением или другой обработкой.

Выделяют две составляющие случайной погрешности измерения координат:

1) инструментальную составляющую – оценивается половиной величины дискретности отсчета (цены деления измерительной шкалы) и обычно в современных приборах пренебрежимо мало влияет на точность измерений;

2) пеленгационную составляющую – характеризует точность установки преобразователя в положение измерения, т. е. в положение, соответствующее максимуму эхосигнала.

В положении 1 на рис. 4.3 дефект озвучивается в направлении акустической оси, а в положении 2 – каким-либо другим лучом диаграммы направленности. Пеленгационная ошибка в первую очередь определяется шириной диаграммы направленности. С увеличением ширины диаграммы направленности пеленгационная ошибка растет.

Рис. 4.3. Пеленгационная составляющая погрешности измерения

координат отражателя

Известна приближенная формула

Δφ  (0,10,2) φ_0,8. (4.4)

Для уменьшения случайной погрешности измерения координат в целом необходимо:

1) иметь малую цену деления измерительной шкалы;

2) тщательно устанавливать преобразователь в положение максимума эхосигнала, причем использовать преобразователь с возможно более узкой диаграммой направленности;

3) при необходимости производить неоднократные измерения с последующим усреднением результата.

Систематическая погрешность появляется при отклонении истинных значений параметров, входящих в расчетные выражения для координат, от их номинальных значений:

1.  = 0º – формула (4.1).

С_l зависит от химического состава и технологии производства материала, а также от температуры; погрешность – ΔС_l;

ΔТ – ошибка измерения временных интервалов.

2.   0º – формулы (4.2), (4.3).

ΔС_t и ΔТ – природа ошибок, как при  = 0º;

Δt_n – причины: изменение пути в призме из-за истирания; изменение скорости звука в призме от температуры;

Δ связано с изменением угла (Δ) из-за истирания призмы, а также со случайным подъемом призмы, температурными изменениями скоростей звука и влиянием затухания.

Изменение угла ввода луча в металл вследствие изменения температуры призмы (рис. 4.4) определяется температурным коэффициентом скорости, показывающим изменение скорости звука в призме на один градус изменения температуры.

Рис. 4.4. Зависимость угла ввода луча от температуры призмы

( = 50°, призма из оргстекла)

Для продольной волны в оргстекле температурный коэффициент скорости при температуре 0–40º составляет с_l = –3м /c·град. Температурное изменение угла ввода тем значительнее, чем больше угол ввода луча.

Оценить влияние температуры на угол ввода можно по данным табл. 4.1.

Таблица 4.1