3 Акустический тракт эхоимпульсного метода

3.1 Отражение от малого плоского дефекта: расчет амплитуды эхосигнала, влияние параметров дефекта

Как указывалось ранее, для расчета акустического тракта могут использоваться различные физические модели и соответствующие им допущения. Воспользуемся коротковолновым (лучевым) приближением, обеспечивающим достаточную точность при решении большинства инженерных задач. Пренебрежем также трансформацией волн («жидкостное» приближение), что вполне оправдано, когда углы падения волн на границы раздела близки к нормали.

В качестве примера рассмотрим расчет акустического тракта эхометода для полого диска, ориентированного перпендикулярно акустической оси совмещенного нормального (прямого) преобразователя. Отражатель расположен на расстоянии от излучателя, причем r > r_бл (r_бл – протяженность ближней зоны); размер отражателя удовлетворяет неравенству , где  – радиус поперечного сечения основного лепестка диаграммы направленности излучателя на расстоянии  . Положим, что длительность импульса достаточно велика, чтобы рассматривать режим излучения как квазистационарный.

Рассчитать акустический тракт можно методом Кирхгофа, приняв каждую точку излучателя за источник волн с амплитудой давления Р₀, а каждую точку отражателя – за вторичный источник, возбуждающий волну с амплитудой, равной амплитуде падающей волны, умноженной на коэффициент отражения R_b. Любая точка, лежащая вне диска, излучателем волн не является.

С учетом принятых допущений давление в волне, создаваемой точечным источником гармонических упругих колебаний на расстоянии r, выражается известной формулой

Р = Р₀ e^–jkr/jλr.

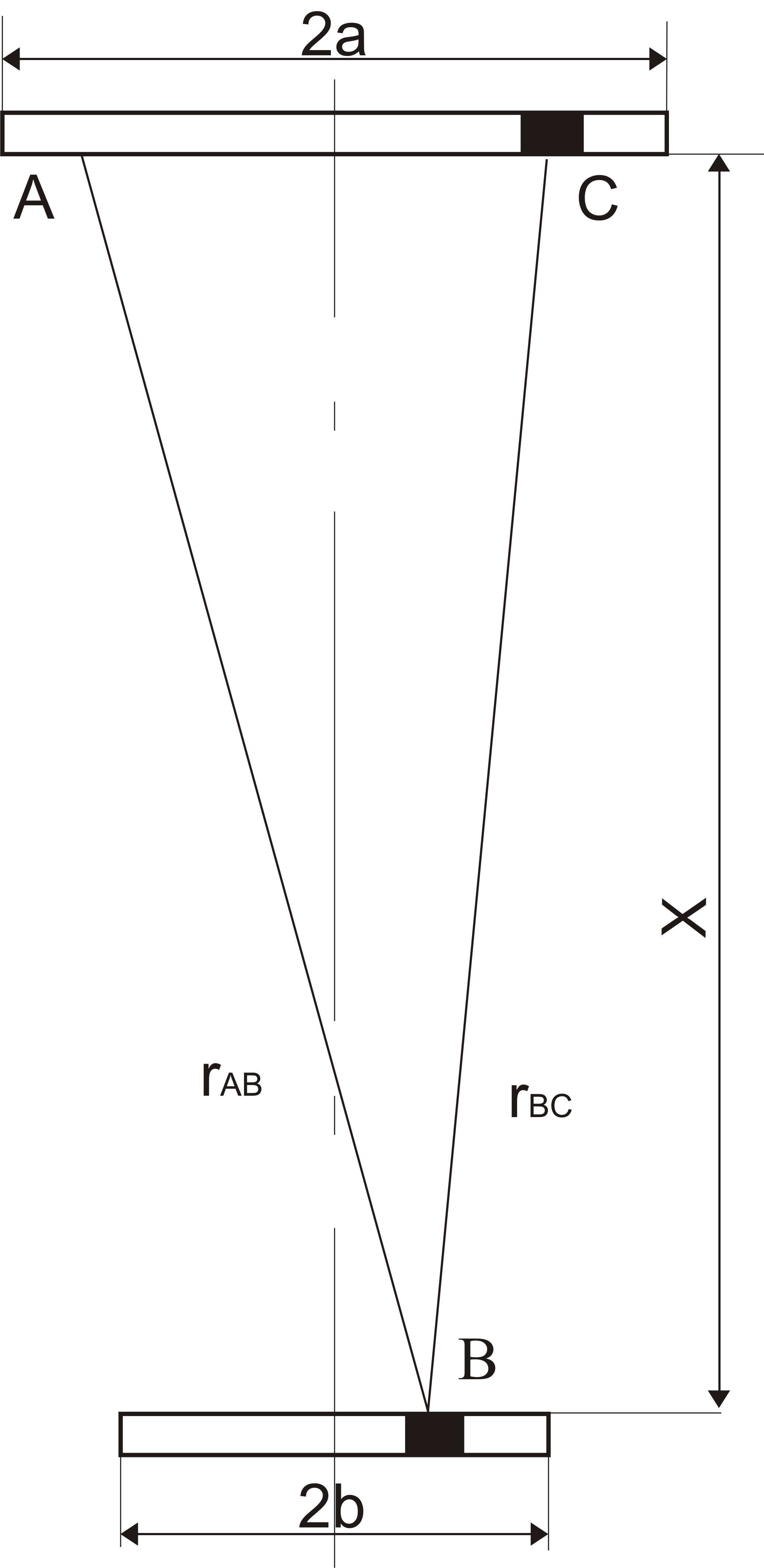
В таком случае в соответствии со схемой, приведенной на рис. 3.1, поле, создаваемое произвольной точкой А излучателя, в произвольной точке В отражателя имеет вид

Р_AB = Р₀exp(–jkr_AB)/jλr_АВ.

Далее, учитывая суммарное воздействие всех точек излучателя, интегрируем по его площади (Sa) и получаем давление, создаваемое излучателем в точке В отражателя: РВ = Р0∫exp(–jkrAB)/jλrАВ dSa = Р0J, где J – интеграл, описывающий поле излучения. Рассматривая теперь точку В отражателя как вторичный источник отраженного поля, создающий давление в точке С преобразователя, работающего в режиме приема, аналогично записанному выше получим РC = Р0 Rb J ∫exp(–jkrBC)/jλrВС dSb.

Рис. 3.1. Схема к расчету акустического тракта эхометода для прямого преобразователя

Учитывая далее, что электрический эхосигнал формируется в результате усреднения воздействий на все точки приемного преобразователя, и принимая во внимание, что в рассматриваемом случае излучатель и приемник совмещены, запишем

Р_д = 1/S_a ∫Р_C dS_a.

Для b << a можно считать, что сомножитель exp(–jkr_BC)/jλr_ВС мало меняется при интегрировании по S_b и может быть вынесен из-под интеграла. (Это соответствует допущению, что все точки вторичного излучателя расположены в геометрическом центре отражателя.) В таком случае выражение для Р_д приводится к виду

. (3.1)

При использовании преобразователя с круглой пластиной J для дальней зоны поля излучателя имеет вид

(3.2)

Для полого диска принимают R_b = 1, поэтому

(3.3)

Учет затухания производят введением в (3.3) экспоненциального множителя:

(3.4)

Таким образом, в дальней зоне поля преобразователя амплитуда отражения от малого плоского дефекта размером более длины волны пропорциональна его площади и площади преобразователя, а также обратно пропорциональна квадрату расстояния до отражателя.

При увеличении размера отражателя выражение (3.2), а значит, и (3.4), нарушается в связи с тем, что излучатель попадает в ближнюю зону отражателя, рассматриваемого как вторичный излучатель. В частности, при преобразователь находится на границе ближней зоны отражателя, что приводит к максимуму функции (рис. 3.2).

Рис. 3.2. Зависимость амплитуды эхосигнала от размера дискового отражателя

Все изложенное справедливо для случая нормального падения волны на диск. При отклонении от нормального падения (рис. 3.3) амплитуда отраженного сигнала довольно быстро спадает, причем скорость спада зависит от размера отражателя (чем он больше, тем быстрее уменьшается амплитуда). Дальнейшее увеличение угла падения сопровождается осцилляциями амплитуды эхосигнала (кривая 1), которые обусловлены многолепестковой формой диаграммы рассеяния диска, однако сглаживаются для импульсного режима (кривая 2).

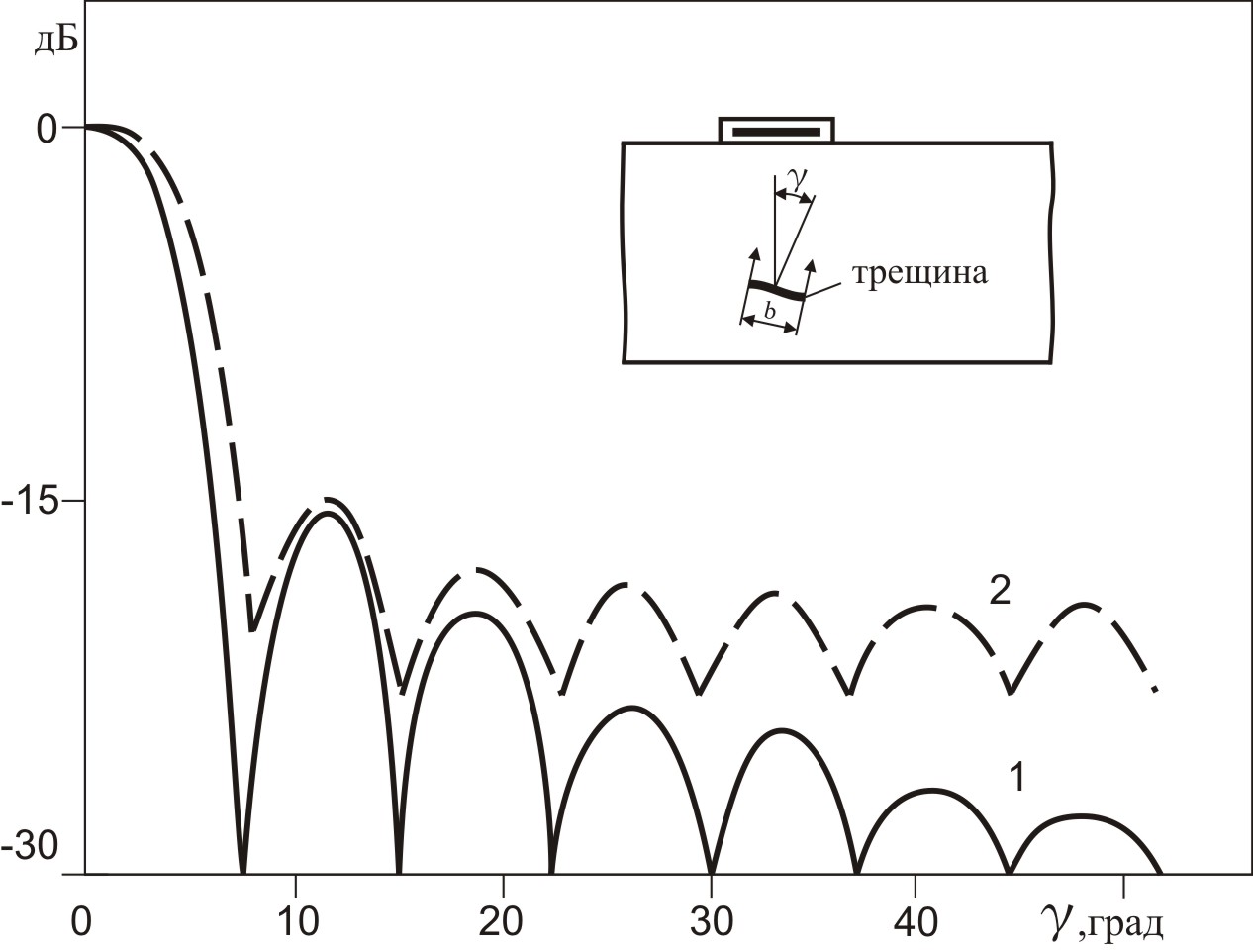
Рис. 3.3. Зависимость амплитуды эхосигнала от угла наклона дискового отражателя в непрерывном (1) и импульсном (2) режимах

Импульсный режим работы излучателя в общем случае приводит к сглаживанию всех интерференционных эффектов, т. е. к сглаживанию всех осцилляций амплитуды эхосигнала. Формально импульсный режим учитывают, используя представление импульса в виде бесконечного набора гармонических волн разной амплитуды (частотное преобразование Фурье) или разложения по другим волновым формам (например, вейвлет-преобразование).

Учет конечных размеров ультразвукового пучка и представление его в виде бесконечного набора плоских волн, распространяющихся под разными углами (пространственное преобразование Фурье), позволяет дополнительно уточнить анализ поля рассеяния и объяснить ряд новых эффектов. Например, в этом случае теоретически доказывается известный экспериментальный факт отражения обратно к излучателю трансформированных упругих волн при озвучивании округлого отражателя.

Рассмотрение дифракционной модели рассеяния волн плоскостным отражателем позволяет заметно сблизить теоретические и экспериментальные результаты. При этом суммарное поле описывают двумя компонентами – геометроакустической и дифракционной. Первая характеризует отражение от плоскости несплошности, вторая – рассеяние на ребрах (вершинах) отражателя. При переходе из освещенной области в тень геометроакустическая составляющая поля скачком уменьшается до нуля, а дифракционная резко возрастает. Вклад каждой составляющей в суммарное поле рассеяния определяется в основном волновым размером отражателя и углом озвучивания.