4.6 Условные размеры дефектов

Все рассмотренные измеряемые характеристики были связаны с положением преобразователя, соответствующим максимальной амплитуде эхосигнала.

Для получения дополнительной информации о дефекте (о его форме и ориентации) делают оценку ширины огибающей на некотором заданном уровне – измерение линейных условных размеров дефекта. Методика измерения применительно к контролю сварных швов иллюстрирована рис. 4.10.

Условную ширину ΔX и условную высоту ΔН определяют при перемещении преобразователя в плоскости падения, она соответствует расстоянию между двумя «крайними» положениями преобразователя и разности показаний глубиномера в этих положениях соответственно.

Под условной протяженностью ΔL понимают расстояние между двумя «крайними» положениями преобразователя при перемещении преобразователя перпендикулярно плоскости падения.

Под «крайними» понимают положения преобразователя, при которых амплитуда эхосигнала от дефекта достигает определенного заданного уровня.

Рис. 4.10. Схема измерения условных размеров дефектов

Выражения для условных размеров дефекта могут быть получены несложным геометрическим построением:

ΔX = (H + b · cosγ) · tgα_II – (H – b · cosγ) · tgα_I + 2b · sinγ; (4.8)

ΔH = H (secα_II – secα_I )cosα₀ + b (secα_II + secα_I )cosα₀cosγ; (4.9)

ΔL = 2Htgφ/cos α₀ + l. (4.10)

Здесь использованы обозначения, принятые в § 2, а также следующие: α_I, α_II – углы озвучивания кромок дефекта в «крайних» положениях преобразователя в плоскости падения; φ_I, φ_II – то же, в дополнительной плоскости; l – протяженность дефекта в дополнительной плоскости.

Для ненаправленного отражателя размеры b и l можно принять равными нулю, и формулы (4.8) – (4.10) принимают вид:

ΔX = H (tgα_II – tgα_I ); (4.11)

ΔH = H (secα_II – secα_I )cosα₀; (4.12)

ΔL = 2Htgφ/cos α₀. (4.13)

Значения α_I, α_II, φ_I, φ_II зависят от того, как заданы «крайние» положения преобразователя, которые определяются способом измерения условных размеров.

4.7 Способы измерения условных размеров дефектов

Существуют два основных способа измерения условных размеров:

I. Относительный способ.

При этом способе уровень измерения «привязывается» к максимальному сигналу. Таким образом, за «крайнее» положение преобразователя принимают такое, при котором амплитуда эхосигнала от дефекта (N_д) уменьшилась в определенное число раз относительно максимальной.

Пусть задан уровень измерения условных размеров – относительный уровень отсечки – А = 0,5. В этом случае для определения, например, ΔХ_д необходимо:

1) найти положение, соответствующее максимуму и измерить N_д;

2) уменьшить показания аттенюатора на 6 дБ, т. е. установить значение (N_д – 6);

3) сместить преобразователь от дефекта до положения, при котором вершина сигнала вернется на уровень измерения; здесь отметить первое «крайнее» положение; ему соответствует значение Х₂;

4) сместить преобразователь к дефекту и аналогично найти второе «крайнее» положение – ему соответствует значение Х₁;

5) вычислить ΔХ_д = Х₂ – Х₁.

ΔХ и ΔL измеряют линейкой, ΔН – с помощью глубиномера. Поскольку при этом способе меняют показания аттенюатора, его полное название – способ измерения условного размера при переменной чувствительности и постоянном уровне отсечки.

При использовании современных приборов процедура измерения относительным способом может быть заметно проще вышеприведенной вследствие наличия блока цифрового отсчета амплитуд и использования различных вариантов обработки полученной дефектоскопической информации. Однако для любых дефектоскопов измерения на уровне 6 дБ облегчаются потому, что разница в амплитудах сигналов, достигающих верхней горизонтали на экране и средней линии, а также средней линии и второй снизу горизонтали, составляет 6 дБ.

II. Абсолютный способ.

При этом способе измерения за «крайние» положения преобразователя принимают такие, при которых амплитуда эхосигнала от дефекта уменьшается до определенного, наперед заданного уровня, не зависящего от максимального значения эхосигнала. Обычно уровень измерений абсолютным способом однозначно привязывают к уровню чувствительности. Процедура измерения абсолютным способом сводится к определению положений преобразователя, в которых вершина эхосигнала на экране достигает принятого уровня измерений.

Рассмотрим зависимости условных размеров от основных факторов.

1. Зависимость условного размера от размера отражателя.

Проанализируем ее на примере отражателей округлой формы.

Пусть на некоторой глубине Н залегают несколько округлых отражателей радиуса b, причем b₃  b₂  b₁ (рис. 4.11, а). Все они находятся в дальней зоне; разницей расстояний от излучателя до отражателя при увеличении b пренебрегаем.

а)

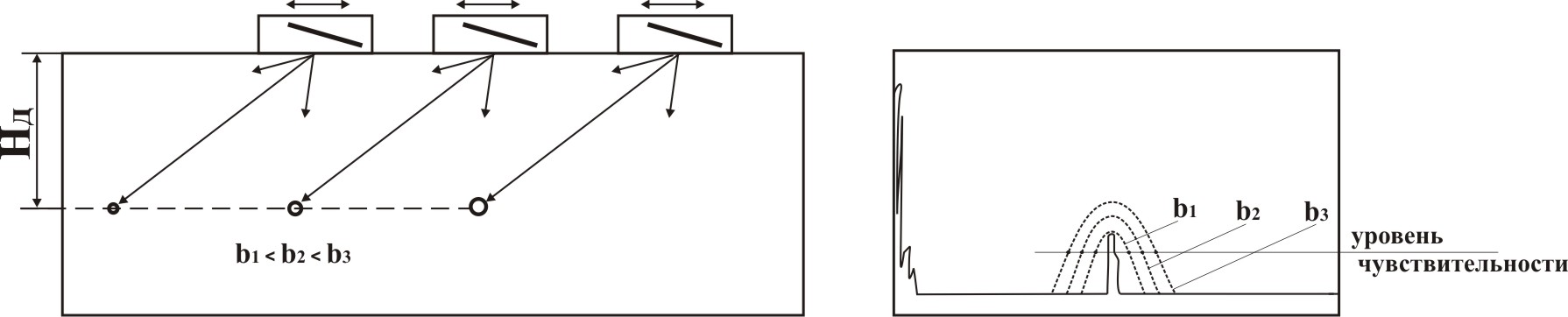
б)

Рис. 4.11. Огибающие амплитуду эхосигналов от отражателей округлой формы

Экспериментально несложно показать, что при абсолютном способе измерений увеличение реального размера такого отражателя приводит к росту условного размера, так как амплитуда при переходе от первого дефекта к третьему растет, эквивалентная площадь растет, и ширина огибающей амплитуд эхосигналов при измерении на одном и том же фиксированном уровне также увеличивается.

При относительном способе измерений необходимо помнить, что принципиально огибающие амплитуд эхосигналов в этом случае отличаются только максимумами, а измерения начинают с определения N_д.

Итак, после определения N_д, т. е. регулировки усиления таким образом, чтобы максимум эхосигнала достиг принятого уровня измерений, огибающие трех отражателей сливаются, хотя N_д1  N_д2  N_д3. Раз огибающие совпадают, значит, условный размер, измеренный относительным способом, при возрастании b не увеличивается.

Вид зависимости анализируемой функции для округлых отражателей приведен на рис. 4.12.

Отметим, что такой ход кривых довольно быстро нарушается в связи с тем, что излучатель попадает в ближнюю зону отражателя, являющегося вторичным излучателем. Этот механизм имеет место при анализе любых функциональных зависимостей, когда в качестве аргумента берется величина b.

Рис. 4.12. Зависимость ΔХ_д от размера ненаправленного отражателя при измерении относительным и абсолютным способами

Для плоскостных отражателей зависимость ΔХ(b) более сложная и должна учитывать ориентацию плоскостного дефекта, остроту его кромок и т. д. В связи с этим невозможно однозначно сказать, какой вид имеет график ΔХ(b) для плоскостного отражателя как при первом, так и при втором способе измерения.

2. Зависимость условного размера от глубины залегания отражателя.

Принципиальное отличие зависимости ΔХ(H) от рассмотренной выше заключается в следующем: нельзя утверждать, что для отражателей любой формы при возрастании Н форма огибающей амплитуд эхо-сигналов остается одинаковой. С другой стороны, с увеличением Н, безу-словно, увеличивается поперечное сечение пучка, что приводит к возрастанию условного размера и при абсолютном и при относительном способе измерения. При отсутствии системы временной регулировки чувствительности (ВРЧ), начиная с некоторой Н, условный размер, измеренный абсолютным способом, начинает уменьшаться просто из-за нехватки чувствительности, поэтому качественно данную зависимость можно изобразить следующим образом (рис. 4.13).

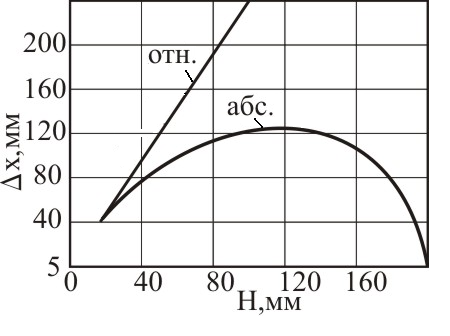
Рис. 4.13. Зависимость ΔХ_д от глубины залегания ненаправленного отражателя при измерении относительным и абсолютным способами (без настройки ВРЧ)

3. Зависимость условного размера от уровня измерения или относительного уровня отсечки.

При увеличении уровня измерения (чувствительности) или относительного уровня отсечки величина условного размера, независимо от способа измерения, уменьшается (рис. 4.14).

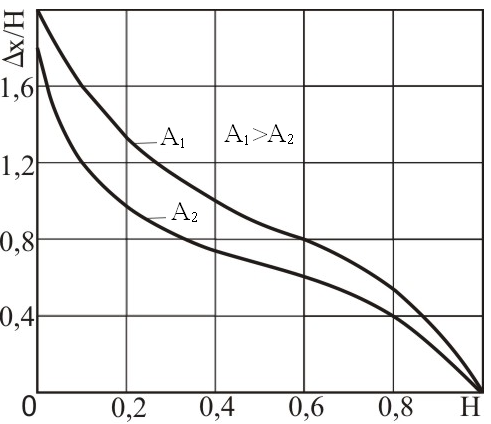
Рис. 4.14. Зависимость отношения ΔХ_д к глубине H залегания ненаправленного отражателя от относительного уровня отсечки А при измерении относительным способом

Зависимости условной высоты и условной протяженности от основных факторов качественно такие же, как и для условной ширины (ΔХ).

Погрешность измерения условных размеров может быть представлена через погрешность определения координат мнимых кромок дефекта. Поэтому природа погрешностей та же, что и при определении координат Н_д, L_д, но суммарная погрешность рассчитывается по более сложным формулам.

В разных алгоритмах оценки качества изделия используют разное сочетание измеряемых характеристик. При этом разбраковка может производиться как по одному отдельно взятому дефекту (с помощью описанных выше характеристик), так и по совокупности дефектов с помощью таких измеряемых характеристик, как количество дефектов на единице длины изделия и условное расстояние между соседними дефектами Δl, которое измеряют в крайних положениях при оценке ΔL₁ и ΔL₂.

В дополнение к основным измеряемым характеристикам дефектов рассматриваются и дополнительные, которые оценивают не отдельный дефект, а совокупность дефектов. Это условное расстояние между соседними дефектами и количество дефектов на единицу длины изделия.

Для распознавания образа и оценки истинного размера дефекта используют еще целый ряд дополнительных измеряемых характеристик. Они рассмотрены далее в параграфе, посвященном методам идентификации дефектов.