
Работы / laba 5
.docxФЕДЕРАЛЬНОЕ АГЕНСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА
Федеральное государственное бюджетное образовательное учреждение высшего образования
«ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ ИМПЕРАТОРА АЛЕКСАНДРА 1»
КАФЕДРА «Методы и приборы неразрушающего контроля»
Дисциплина «Обнаружение и фильтрация сигналов»
Отчёт
По лабораторной работе № 5
«Исследование работы цифрового фильтра»
ВАРИАНТ 5
Выполнил студент: Сабитов И.А.
Факультет: АИТ
Проверил: Кособоков Д.В.
Санкт-Петербург 2020
Цель работы:
Практическое освоение методов расчета нерекурсивных цифровых фильтров. Исследование свойств синтезированных фильтров.
Ход выполнения работы:
В начале работы был проведен ручной расчет коэффициентов ak фильтра нижних частот. Однако и перед этим необходимо рассчитать Δt и Δτ.
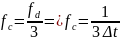

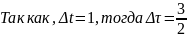
При порядке фильтра N=4 коэффициенты ak будут равны:
a0=0.667 a1=0.2757 a2=-0.1378 a3=-2,5988e-17 а4=0,0689
Эти же коэффициенты совпали с графиком ИПХ, представленном на рисунке 1.
Далее был получен график передаточной функции цифрового фильтра НЧ (рисунок 2).
По аналогии, с графиками из предыдущей лабораторной работы и опираясь на конспекты лекций (как на СДО, так и найденные на просторах интернета), можно сделать вывод, что мы стремимся к более резкому спаду характеристики, а в нашем случае она… Слишком пологая. Такой «колокольный» вид характеристики нас не устраивает.
Для того, чтобы спад характеристики был более резкий необходимо увеличить порядок фильтра, что мы и делаем в следующем пункте(рисунок3)
Далее, чтобы сгладить неравномерность в области пропускания фильтра мы использовали треугольное окно (рисунок 4)
Последнем пунктом лабораторной работы стало получение АЧХ полосового фильтра.
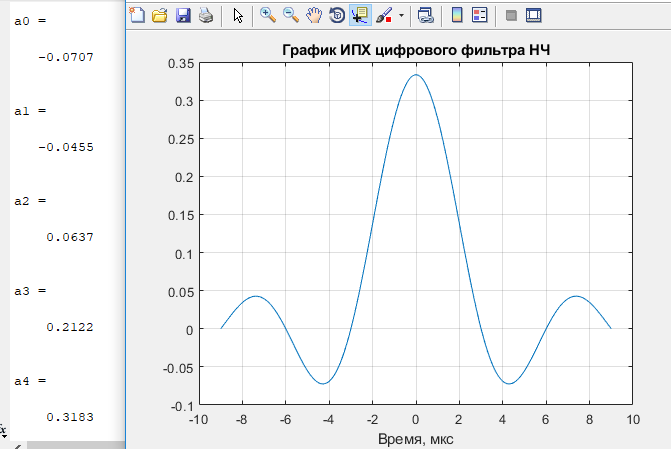
Рисунок 1 – График ИПХ цифрового фильтра НЧ
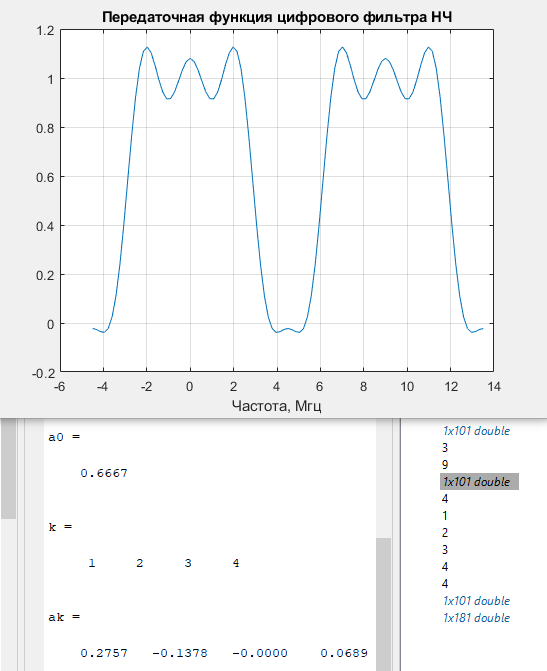
Рисунок 2 – График передаточной функции цифрового фильтра НЧ. Порядок фильтра N=8.
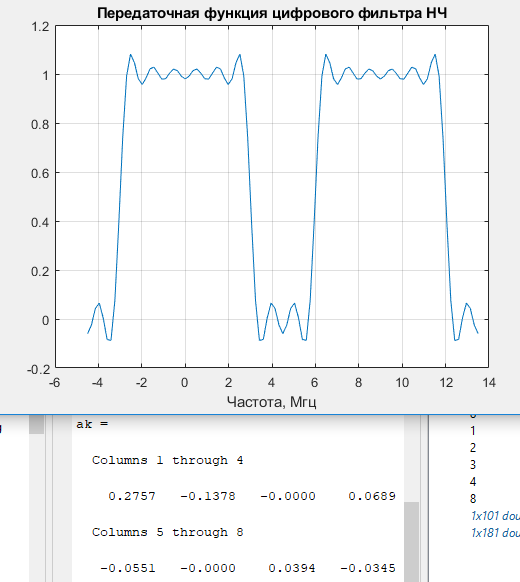
Рисунок 3 – График передаточной функции цифрового фильтра НЧ, с порядком N=4.
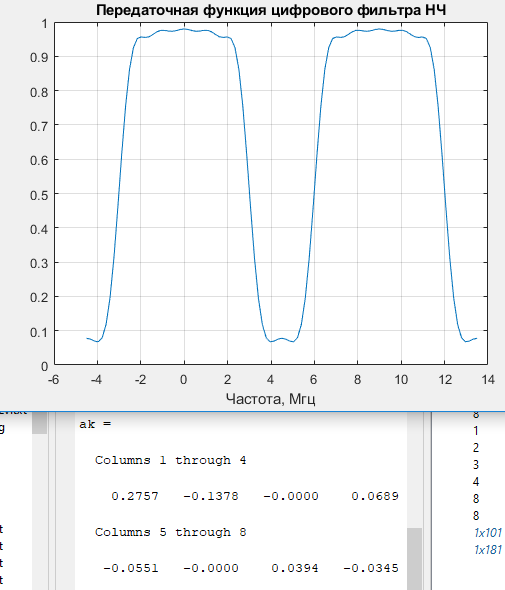
Рисунок 4 – График передаточной функции цифрового фильтра НЧ, после применения к ней треугольного окна.
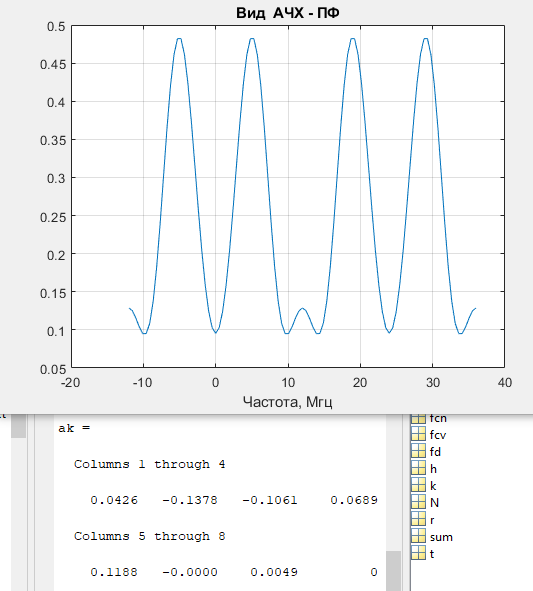
Рисунок 5 – АЧХ полосового фильтра.
Коды программ
Программа для пункта 2.2
fd=9;
dTau =3; % расстояние между нулями
dt=1;
fc = 1/(2*dTau); % частота среза через, выраженная через
t = -3*dTau : 0.1 : 3*dTau;
h = 2*fc*sinc(2*fc*t);
a0=h(46)
a1=h(56)
a2=h(66)
a3=h(76)
a4=h(86)
plot(t, h), grid on; % график ИПХ
title( 'График ИПХ цифрового фильтра НЧ' );
xlabel( 'Время, мкс' );
Программа для пункта 2.3
N =8; % порядок фильтра
fd =9; % частота дискретизации
fc=3;
a0 =2*(fc/fd) % нулевой коэффициент фильтра
k=(1:N)
ak(k) = 2*(fc/fd)*sinc(2*(fc/fd)*k) % коэффициенты фильтра
dt = 1; % шаг дискретизации
f = -0.5 : 0.02 : 1.5; % диапазон частот
sum = 0;
for k = 1:N, sum = sum + ak(k)*cos(2*pi*f*k*dt); end;
h = a0 + 2*sum; % частотная характеристика
plot(f*fd, h), grid on; % построение графика
title('Передаточная функция цифрового фильтра НЧ' );
xlabel( 'Частота, Мгц' );
Программа для пункта 2.4
N =8 ; % порядок фильтра
fd =9 ; % частота дискретизации
fc=3;
a0 =2*(fc/fd) ; % нулевой коэффициент фильтра
k=(1:N)
ak(k) = 2*(fc/fd)*sinc(2*(fc/fd)*k) % коэффициенты фильтра
dt = 1; % шаг дискретизации
f = -0.5 : 0.02 : 1.5; % диапазон частот
sum = 0;
for k = 1:N, sum = sum + ak(k)*cos(2*pi*f*k*dt); end;
h = a0 + 2*sum; % частотная характеристика
plot(f*fd, h), grid on; % построение графика
title('Передаточная функция цифрового фильтра НЧ' );
xlabel( 'Частота, Мгц' );
Программа для пункта 2.5
N =8 ; % порядок фильтра
fd =9 ; % частота дискретизации
fc=3;
a0 =2*(fc/fd) ; % нулевой коэффициент фильтра
k=(1:N)
ak(k) = 2*(fc/fd)*sinc(2*(fc/fd)*k) % коэффициенты фильтра
dt = 1; % шаг дискретизации
% умножение на треугольное окно
for r = 1:N; ak(r) = ak(r)*(1-r/N); end;
f = -0.5 : 0.02 : 1.5; % диапазон частот
sum = 0;
for k = 1:N, sum = sum + ak(k)*cos(2*pi*f*k*dt); end;
h = a0 + 2*sum; % частотная характеристика
plot(f*fd, h), grid on; % построение графика
title('Передаточная функция цифрового фильтра НЧ' );
xlabel( 'Частота, Мгц' );
Программа для пункта 2.6
N =5; % порядок фильтра
fd =24 ; % частота дискретизации
fcv=6;
fcn=4;
a0 = 2*(fc/fd) ; % нулевой коэффициент фильтра
k=(1:N)
akv(k) = 2*(fcv/fd)*sinc(2*(fcv/fd)*k)
akn(k) = 2*(fcn/fd)*sinc(2*(fcn/fd)*k)
ak(k) = akv(k)- akn(k) % коэффициенты фильтра
dt = 1; % шаг дискретизации
% умножение на треугольное окно
for r = 1:N; ak(r) = ak(r)*(1-r/N); end;
f = -0.5 : 0.02 : 1.5; % диапазон частот
sum = 0;
for k = 1:N, sum = sum + ak(k)*cos(2*pi*f*k*dt); end;
h = a0 + 2*sum; % частотная характеристика
plot(f*fd, h), grid on; % построение графика
title('Вид АЧХ - ПФ' );
xlabel( 'Частота, Мгц' );
Выводы
В ходе лабораторной работы были освоены основные методы расчета нерекурсивных цифровых фильтров. Также было проведено исследование свойств синтезированных фильтров, рассмотрено и проанализировано влияние треугольного окна на неравномерности в области пропускания фильтра, вызванные повышением его порядка и построена АЧХ для фильтра высоких частот.
