РОСЖЕЛДОР
Государственное образовательное учреждение
высшего профессионального образования
«Ростовский государственный университет путей сообщения»
(РГУПС)
Т.В. Суворова, О.А. Беляк, А.Н. Хоперский
ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ
Учебно-методическое пособие
Ростов-на-Дону
2008
УДК 512.2
Суворова, Т. В.
Элементы теории поля: учебно-методическое пособие / Т.В. Суворова; О.А. Беляк, А.Н. Хоперский; Рост. гос. ун-т путей сообщения. – Ростов н/Д, 2008. ─ 28 с. Библиогр. : 10 назв.
Приведены сведения о скалярных и векторных полях и их основных характеристиках: производной по направлению, градиенте, потоке, циркуляции. Даны понятия о соленоидальных и потенциальных полях. Приведены задания для самостоятельной работы. Учебно-методическое пособие предназначено для студентов второго курса технических специальностей РГУПС.
Рецензент д-р техн. наук, проф. К.С. Ахвердиев (РГУПС)
Учебное издание
Суворова Татьяна Виссарионовна
Беляк Ольга Александровна
Хоперский Алексей Николаевич
ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ
Учебно-методическое пособие
Редактор А.И. Гончаров
Техническое редактирование и корректура А.И. Гончаров
Подписано в печать 03.06.2008. Формат 60х84/16
Бумага офсетная. Ризография. Усл. печ.л. 1,63
Уч.-изд.л. 1,55. Тираж 100 экз. Изд. № 96. Заказ №
Ростовский государственный университет сообщения.
Ризография РГУПС.
Адрес университета; 344038, г. Ростов н/Д, пл. Ростовского Стрелкового Полка Народного ополчения, 2
© Ростовский государственный университет путей сообщения, 2008
Содержание
Введение
Скалярное поле
Производная по направлению
Градиент скалярного поля
Связь градиента и производной по направлению. Физический смысл градиента
Геометрический смысл градиента
Оператор Гамильтона
Векторное поле
Поток векторного поля
Дивергенция векторного поля
Циркуляция векторного поля
Ротор векторного поля. Формула Стокса
Соленоидальное поле
Потенциальное поле
Вычисление потенциала векторного поля
Гармоническое поле
Задачи для самостоятельного решения
Библиографический список
Введение
К изучению свойств полей приводят многие задачи физики, электротехники, теплообмена, математики, механики, теории фильтрации, гидродинамики и многих других технических дисциплин. Математика изучает общие свойства и характеристики, присущие полям разного происхождения.
В пространстве
задано поле некоторой величины
,
если в каждой точке пространства (или
его части) определено значение этой
величины. Например, при изучении потока
газа приходится исследовать несколько
полей: температурное поле, поле давлений,
поле скоростей. Это скалярные и векторные
поля.
Поле величины называется стационарным или установившимся, если не зависит от времени. В противном случае поле называется нестационарным или неустановившимся.
Для простоты далее будем рассматривать стационарные поля.
Скалярное поле
Пусть
− некоторая область плоскости или
пространства. Если в каждой точке
определена скалярная величина
,
то говорят, что в области
задано скалярное поле.
Обычно поле задается
с помощью функции нескольких переменных
,
называемой скалярной функцией. В
пространстве с декартовыми координатами
.
Примером скалярного поля может служить поле температур объекта, поле электрического потенциала.
Свойства скалярных полей можно наглядно изучать с помощью поверхностей и линий уровня
Поверхностью уровня скалярного поля называется множество точек, в которых функция принимает постоянное значение:
.
(1)
Например, для
скалярного поля, образованного функцией
трех переменных
,
поверхности уровня представляют собой
множество концентрических сфер с центром
в начале координат:
.
Возводя в квадрат
обе части равенства, имеем:
.
В плоском скалярном поле линиями уровня называют кривые, на которых поле принимает постоянное значение
.(2)
На рис. 1 изображены
линии уровня поверхности
и их проекции на плоскость
.
Рис. 1. Линии уровня поверхности и их проекции
на горизонтальную плоскость
Термин «линии уровня» заимствован из картографии, где линии уровня – это линии, на которых высота точек земной поверхности над уровнем моря постоянна. По ним можно судить о характере рельефа местности. Если взять в уравнении (2) постоянные величины, образующие арифметическую прогрессию, то получим ряд линий уровня, по которым можно судить о форме поверхности (рис. 1).
Производная по направлению
Для характеристики
скорости изменения поля
в точке
в
заданном направлении
вводится понятие производной по
направлению.
Пусть
− единичный вектор, имеющий начало в
точке
.
Проведем через точку
прямую, совпадающую с вектором
,
и в направлении вектора
возьмем
на прямой точку
.
Приращение функции
,
возникающее при переходе от точки
к
точке
,
определяется как
.
Тогда
.
Производной по
направлению от функции
в точке
по
направлению
называется предел
.
(3)
Производная по направлению характеризует изменение поля в точке в данном направлении. Если производная положительна, то поле в заданном направлении возрастает, если производная отрицательна − поле в заданном направлении убывает.
Физический смысл
производной по направлению в том,
что она равна мгновенной скорости
изменения поля в точке
по
направлению
.
Полагая, что функция дифференцируема в точке , из формулы (3) и условия дифференцируемости функции получим формулу для вычисления производной по направлению:
. (4)
В случае плоского
поля
и формула (4) принимает вид:
. (5)
Понятие производной
по направлению является обобщением
понятия частных производных
.
Их можно рассматривать как производные
от функции
в направлении координатных осей. Если
вектор
совпадает
с положительным направлением оси Ох,
то в формуле (4) следует положить
тогда
.
Аналогично получаем, что производная
по направлению оси Оу совпадает с
,
в направлении оси Oz
− cовпадает с частной
производной
.
Пример 1. Найти
производную функции
в точке
в
направлении вектора
.
Решение. Вектор
−
единичный, так как
,
поэтому
Вычислим частные
производные функции в точке
.
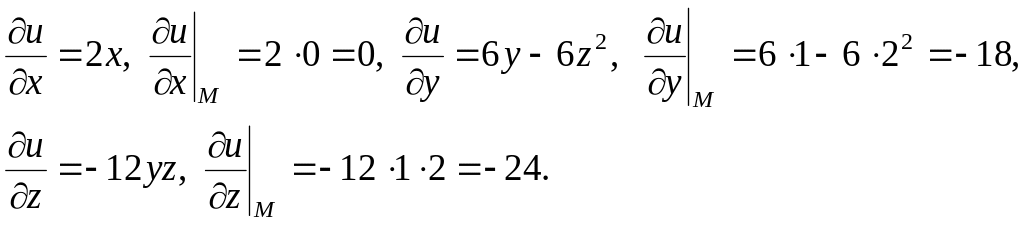
По формуле (4)
получим
Пример 2. Найти
производную функции
в точке
в направлении вектора
,
где
– точка с координатами (3,0).
Решение. Найдем единичный вектор , имеющий данное направление:
Отсюда
Вычислим частные
производные функции в точке
:
По формуле (5) получим
